(paper 14) Contrastive Predictive Coding (CPC)

Representation Learning with Contrastive Predictive Coding

Contents

1. Abstract
2. Contrastive Predictive Coding
   1. Motivation & Intuition
   2. Contrastive Predictive Coding
   3. Info NCE & Mutual Information Estimation

0. Abstract

“Contrastive Predictive Coding (CPC)”

• universal UNsupervised learning approach to extract useful representations from HIGH-dim data

• details

  • by predicting the future in the latent space with autoregressive models
  • use a probabilistic contrastive loss
  • tractable by using negative sampling

1. Contrastive Predictive Coding

(1) Motivation & Intuition

Main intution

• encode the underlying SHARED information between different parts of HIGH-dim signal

  ( + discard LOW-level information & noise )

• Slow features ( = shared info, global structure … )

  • the further in the future, amount of shared info becomes lower

Challenges in predicting high-dim data

• (1) unimodal losses ( ex. MSE, CE ) are not useful

• (2) generative models : computationally intense

  • waste in capturing relationships in data \(x\), ( ignoring context \(c\) )

  • modling \(p(x \mid c)\) directly ?

    \(\rightarrow\) may not be optimal for the purpose of extracting shared info between \(x\) & \(c\)

This paper :

• encode the target \(x\) ( future ) & context \(c\) ( present) into compact distributed vector,

  in a way that maximally preserves the MUTUAL information of \(x\) & \(c\)

• \(I(x ; c)=\sum_{x, c} p(x, c) \log \frac{p(x \mid c)}{p(x)}\).

(2) Contrastive Predictive Coding

a) architecture

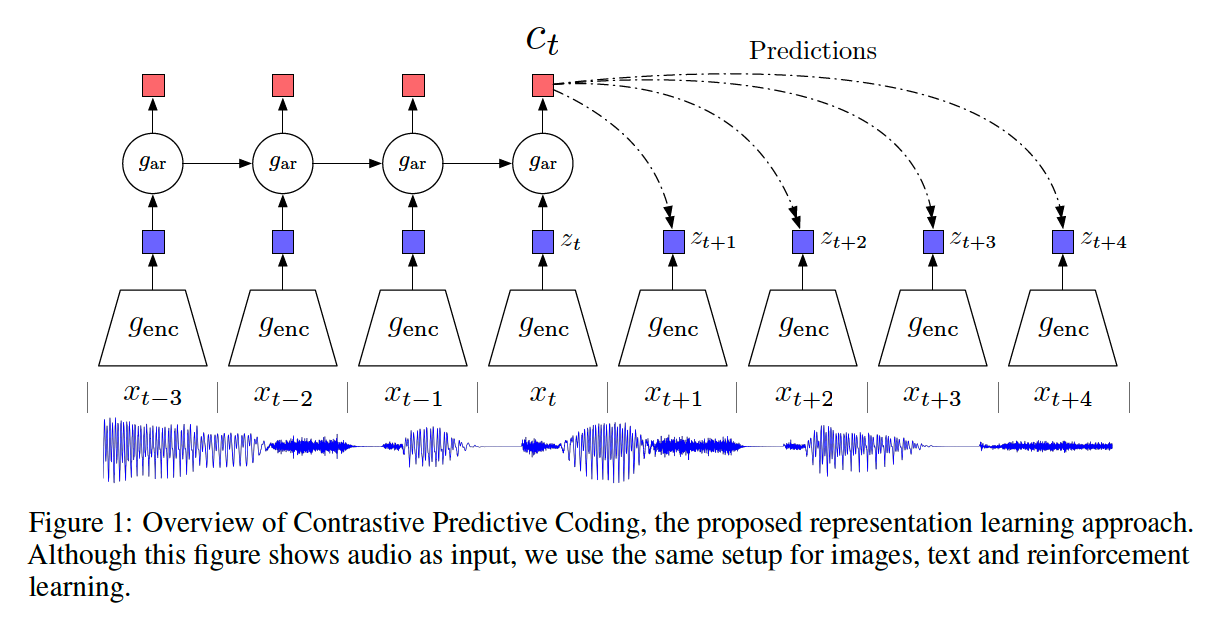
b) notation

Model :

• [encoder] \(g_{\text {enc }}\) ……… \(z_{t}=g_{\text {enc }}\left(x_{t}\right)\)
• [AR model] \(g_{\mathrm{ar}}\) ………. summarizes all \(z_{\leq t}\) in the latent space & produce context \(c_{t}=g_{\mathrm{ar}}\left(z_{\leq t}\right)\)

c) mutual information

do not predict \(x_{t+k}\) directly with generative model \(p_{k}\left(x_{t+k} \mid c_{t}\right)\)

\(\rightarrow\) instead, model a density ratio ( which preserves mutual information between \(x_{t+k}\) & \(c_t\) )

Density ratio

• \(f_{k}\left(x_{t+k}, c_{t}\right) \propto \frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)}\).

  ( \(f\) can be unnroamlized )

• use a log-bilinear model, \(f_{k}\left(x_{t+k}, c_{t}\right)=\exp \left(z_{t+k}^{T} W_{k} c_{t}\right)\)

  • linear transformation \(W_{k}^{T} c_{t}\) is used for prediction, with different \(W_k\) for every step \(k\)

Working in LOW-dim

• by using density ratio & inferring \(z_{t+k}\) with encoder,

  \(\rightarrow\) relieve the model from modeling the high-dim \(x\)

(3) Info NCE & Mutual Information Estimation

Encoder & AR model : jointly optimized, based on NCE ( = InfoNCE )

Notation

• \(X=\left\{x_{1}, \ldots x_{N}\right\}\) of \(N\) random samples
• pos & neg
  • 1 pos ~ \(p\left(x_{t+k} \mid c_{t}\right)\)
  • (N-1) neg ~ \(p\left(x_{t+k}\right)\)

InfoNCE loss : \(\mathcal{L}_{\mathrm{N}}=-\underset{X}{\mathbb{E}}\left[\log \frac{f_{k}\left(x_{t+k}, c_{t}\right)}{\sum_{x_{j} \in X} f_{k}\left(x_{j}, c_{t}\right)}\right]\)

• optimizing InfoNCE = estimating density ratio

Optimal probability for this loss : \(p\left(d=i \mid X, c_{t}\right)\)

• meaning of \([d=i]\) : \(x_i\) is positive sample
• \(\begin{aligned} p\left(d=i \mid X, c_{t}\right) &=\frac{p\left(x_{i} \mid c_{t}\right) \prod_{l \neq i} p\left(x_{l}\right)}{\sum_{j=1}^{N} p\left(x_{j} \mid c_{t}\right) \prod_{l \neq j} p\left(x_{l}\right)}=\frac{\frac{p\left(x_{i} \mid c_{t}\right)}{p\left(x_{i}\right)}}{\sum_{j=1}^{N} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}} \end{aligned}\).
  • probability that \(x_i\) was drawn from \(p\left(x_{t+k} \mid c_{t}\right)\), rather than \(p\left(x_{t+k}\right)\)

minimizing InfoNCE loss (\(L_N\)) = maximize the lower bound of MI (Mutual Information)

\(I\left(x_{t+k}, c_{t}\right) \geq \log (N)-\mathcal{L}_{\mathrm{N}}\).

( proof )

\(\begin{aligned} \mathcal{L}_{\mathrm{N}}^{\mathrm{opt}} &=-\underset{X}{\mathbb{E}} \log \left[\frac{\frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)}}{\frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)}+\sum_{x_{j} \in X_{\text {neg }}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}}\right] \\ &=\underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)} \sum_{x_{j} \in X_{\text {neg }}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}\right] \\ & \approx \underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)}(N-1) \underset{x_{j}}{\mathbb{E}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}\right] \\ &=\underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)}(N-1)\right] \\ & \geq \underset{X}{\mathbb{E}} \log \left[\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)} N\right] \\ &=-I\left(x_{t+k}, c_{t}\right)+\log (N), \end{aligned}\).