VisionTS++; Cross-Modal TS Foundation Model with Continual Pre-trained Visual Backbones

VisionTS++: Cross-Modal TS Foundation Model with Continual Pre-trained Visual Backbones

https://github.com/HALF111/VisionTSpp

Contents

1. Abstract
2. Introduction
3. Related Works
4. Preliminaries
5. Methodology (Brief)
6. Methodology (Detail)
7. Experiments
8. Conclusions

0. Abstract

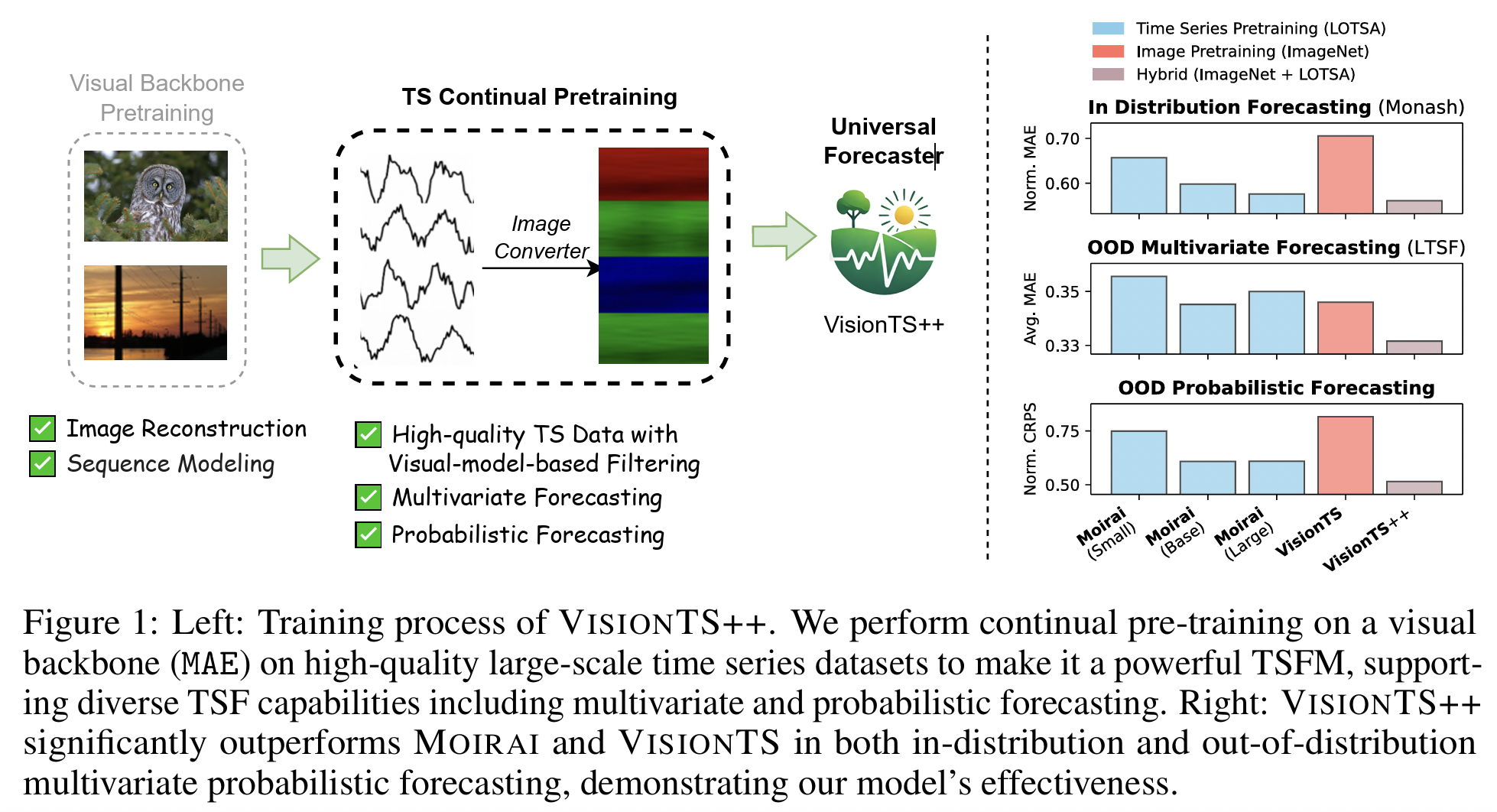
Vision models pre-trained on images can transfer to TS forecasting (TSF).

Challenges:

• Data-modality gap
• Multivariate-forecasting gap
• Probabilistic-forecasting gap.

Propose VisionTS++ with:

• Vision-model-based filtering for high-quality TS data.
• Colorized multivariate conversion into RGB subfigurs.
• Multi-quantile forecasting with parallel heads.

Outperforms specialized TSFMs by 6%–44% MSE reduction, ranks 1st in 9/12 probabilistic forecasting tasks.

1. Introduction

• Foundation models succeed in NLP, CV, TSF.
• Vision models (e.g., MAE) surprisingly strong in zero-shot TSF
• Gaps identified:
  • Data-Modality Gap: Bounded images vs. Unbounded heterogeneous TS.
  • Multivariate-Forecasting Gap: RGB (3 channels) vs. Arbitrary M variates.
  • Probabilistic-Forecasting Gap: Deterministic outputs vs. Uncertainty-aware forecasts
• Goal: Adapt vision backbones to TSF while preserving pre-trained visual knowledge.

2. Related Works

TSFM

• Non-vision: Moirai, Chronos, TimesFM, Timer, Moment, Time-MoE.
• Vision: Earlier CNN-based methods, ViTST, VisionTS.

VisionTS

• [VisionTS] Reformulates TSF as image reconstruction
  • But does not fully address modality gaps.
• [VisionTS++] Propose competitive TSFM via continual pre-training on visual backbones.

3. Preliminaries

TSF definition:

• Input sequence: \(X_{t-L:t} \in \mathbb{R}^{L \times M}\)
• Forecasting target: \(\hat{X}_{t:t+T} \in \mathbb{R}^{T \times M}\).

Image Reconstruction (MAE):

• Divide image \(W \times W\) into patches \(S = W/N\)
• Mask random patches, reconstruct via ViT encoder-decoder.

4. Methodology (Brief)

1. Vision-model-based Filtering

   • Normalize TS:
     • \(X^{norm}_{t-L:t} = r \cdot \frac{X{t-L:t} - X_{mean}}{X_{std}}, \quad X^{norm}_{t:t+T} = r \cdot \frac{X{t:t+T} - X_{mean}}{X_{std}}\).

   • Use visual data range \(\big[ \frac{0 - I_{mean}}{I_{std}}, \frac{255 - I_{mean}}{I_{std}} \big]\) to filter invalid samples.

   • Default scaling factor: \(r = 0.4\)

2. Colorized Multivariate Conversion

   • Segment each variate into subsequences of periodic length \(P\)

   • Convert to 2D matrix & Stack into subfigures

   • Assign each variate to distinct RGB channel with randomized coloring

     → Supports multi-object analysis

3. Multi-Quantile Forecasting

   • \(h\) parallel heads predict quantiles: - \(q_i = \frac{i}{h+1}, \quad i \in \{1,2,\dots,h\}\).

• Quantile loss (pinball loss):
  • \(E_i = \hat{X}_{t:t+T} - X^{(i)}_{t:t+T}, \quad l_i = \max(q_i \cdot E_i, (q_i - 1)\cdot E_i), \quad L_q = \frac{1}{h} \sum_{i=1}^h l_i\).

5. Methodology (Detail)

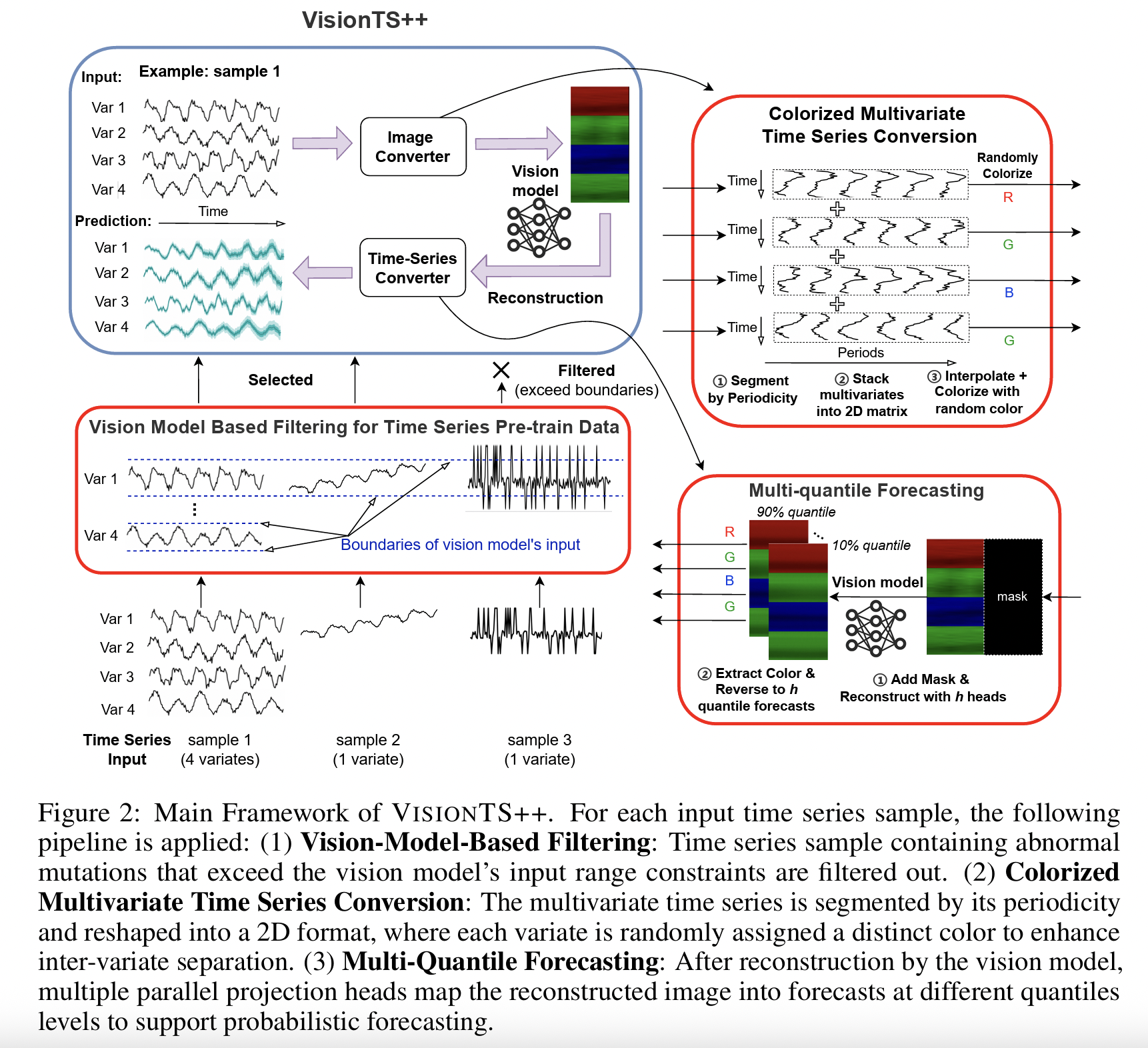
Overview

• VisionTS++ = 기존 VisionTS(TSF → Image Reconstruction) 를 확장.
• 핵심 아이디어:
  1. Vision-model-based Filtering → data-modality gap 완화.
  2. Colorized Multivariate Time Series Conversion → multivariate-forecasting gap 완화.
  3. Multi-Quantile Forecasting → probabilistic-forecasting gap 완화.
• 전체 Pipeline
  • 입력 TS → Filtering → Image Converter (Colorization) → MAE Backbone Reconstruction → Multi-head Quantile Forecast → Time-series Conversion.

(1) Vision-model-based Filtering

a) Challenges

• [Image] pixel ∈ [0, 255], bounded.
• [TS] unbounded (예: extreme spikes, abnormal mutations).

\(\therefore\) 그대로 TS를 Vision backbone에 입력 시, pre-trained visual knowledge를 활용 못 하고 negative transfer 발생

b) Solutions

• Normalize TS: To align with image statistics.
• Filtering Criterion: Discard samples exceeding valid pixel boundaries after normalization.

Step-by-step:

1. 입력 TS
   • \(X_{t-L:t} \in \mathbb{R}^{L \times M}, \quad \hat{X}_{t:t+T} \in \mathbb{R}^{T \times M}\).
2. 평균, 표준편차 계산
   • \(X_{mean}, X_{std} \quad \text{from } X_{t-L:t}\).
3. Normalization + scaling factor \(r < 1\) (empirical best r = 0.4)
   • \(X^{norm}_{t-L:t} = r \cdot \frac{X_{t-L:t} - X_{mean}}{X_{std}}, \quad X^{norm}_{t:t+T} = r \cdot \frac{X_{t:t+T} - X_{mean}}{X_{std}}\).
4. Vision model의 valid pixel 범위 (ImageNet 기준)
   • \(\Big[ \frac{0 - I_{mean}}{I_{std}}, \frac{255 - I_{mean}}{I_{std}} \Big]\).
5. Filtering rule:
   • 모든 값이 이 범위 안에 있으면 retain, 아니면 discard.

효과:

• Out-of-bound sample 제거 → 안정적인 continual pre-training.
• Pre-trained visual knowledge 유지.

(2) Colorized Multivariate Time Series Conversion

a) Challenges

• [Image] RGB (3-channel),
• [MTS] Arbitrary M variates (channels).

\(\therefore\) 단순히 variate별 separate images = computationally heavy, no inter-variate dependency.

b) Solutions

• 각 variate를 하나의 subfigure 로 할당
• 전체 이미지를 여러 “stacked subfigures” 로 구성
• Random RGB channel 할당으로 variates 구분

Step-by-step:

1. Input:

   • \(X_{t-L:t} \in \mathbb{R}^{L \times M}\).

2. Segmentation:

   • 각 variate \(m \in [1, M]\) 에 대해 periodicity \(P\) 단위로 subsequences 분할.

3. Subfigure 변환:

   • \(I^{raw}_m \in \mathbb{R}^{P \times \lfloor L/P \rfloor}\).

4. Resampling:

   • 각 subfigure를 \((P, L/P) → (⌊W/M⌋, W/2)\) 크기로 interpolation.

   • 왼쪽 절반 (W/2): visible (input),
   • 오른쪽 절반 (W/2): masked (prediction).

5. Stack all variates vertically:

   • 최종 shape = \((⌊W/M⌋ × M, W/2)\)

   • (M이 W에 나누어 떨어지지 않으면 zero-padding)

6. Randomized RGB coloring:

   • 각 subfigure → 하나의 RGB channel에 random 배정.
   • 인접 subfigure는 다른 색상 할당 → clear boundary.

효과:

• Multivariate TS = multi-object image.
• MAE의 patch-level attention → variate 간 dependency 학습 가능.
• Random colorization = model이 color semantics에 의존하지 않고 boundary indicator로 학습.

(3) Multi-Quantile Forecasting

a) Challenges

• MAE reconstruction → Deterministic single-point forecast.
• TSF는 uncertainty-aware probabilistic forecast 필요.

b) Solutions

• Parallel reconstruction heads = 각기 다른 quantile 예측.
• Probabilistic forecasting = 여러 quantile point forecasts 조합.

Step-by-step:

1. \(h\)개의 forecasting heads 설정.
   • 각 head → quantile level
   • \[q_i = \frac{i}{h+1}, \quad i \in \{1, 2, \dots, h\}\]
     • 예: \(h=9\) → deciles [10%, 20%, …, 90%].
2. Reconstruction:
   • Vision backbone output → \(h\)개의 reconstructions (이미지)
3. Image-to-TS Conversion:
   • Subfigure 분리 (\(⌊W/M⌋\) → \(M\) variates)
   • RGB channel별 값 추출.
   • Resample back to \((P, ⌊T/P⌋)\)
   • 최종 TS output: \((T, M)\) per head.
4. Training objective = Quantile loss (Pinball loss):
   • \(L_q = \frac{1}{h} \sum_{i=1}^h l_i\).
     • \(l_i = \max(q_i \cdot E_i, (q_i - 1)\cdot E_i)\).
       • \(E_i = \hat{X}_{t:t+T} - X^{(i)}_{t:t+T}\) .

장점:

• Distribution-free (no Gaussian assumption).
• Flexible: head 수 늘리면 quantile coverage 확장.
• Unified: deterministic (median) + probabilistic 예측 모두 가능.

(4) Summary of Methodology

• Vision-model-based Filtering: 데이터 품질 제어, negative transfer 억제.
• Colorized Multivariate Conversion: arbitrary variates 처리, inter-variate dependency 학습.
• Multi-Quantile Forecasting: probabilistic 예측 가능, uncertainty 정량화.
• 모두 non-invasive → MAE 구조 변경 없이 적용 가능.

6. Experiments

• Training:
  • LOTSA dataset (231B obs).
  • Backbone: MAE (base, 112M params), also large (330M), huge (657M).
  • Multi-quantile heads \(h = 9\)
  • 100k steps, AdamW (lr=1e-4).

• Benchmarks: Monash, LTSF, Probabilistic Forecasting (PF).

• Results:
  • In-distribution (Monash): VisionTS++ > VisionTS (+23.2%), > Moirai.
  • Out-of-distribution (LTSF): SOTA in 12/14 cases, 6%–44% lower MSE.
  • Probabilistic Forecasting (PF): Best in 9/12 settings (CRPS, MASE).
• Ablation (Table 4, p.11):
  • Without filtering: +10% error.
  • Without colorization: +7% MSE.
  • Without quantile heads: +12% error.
• Backbone scale (Table 5, p.12): Similar performance across base/large/huge → continual pre-training neutralizes size gap.

7. Conclusions

• VisionTS++ = first vision-pretrained foundation model continually adapted to TS.
• Three key components:
  • Filtering
  • Colorized multivariate conversion
  • Multi-quantile forecasting.
• Outperforms specialized TSFMs across Monash, LTSF, PF benchmarks.
• Future:
  • Multi-modal pre-training
  • Broader TS tasks (classification, anomaly detection), video-based extensions.