Tree-of-Thoughts (ToT)

Tree-of-Thoughts (ToT)

Yao et al., Tree of Thoughts: Deliberate Problem Solving with Large Language Models, NeurIPS 2023

• https://arxiv.org/pdf/2305.10601

1. Motivation

Chain-of-Thought (CoT):

• 핵심: LLM이 reasoning할 때 한 줄(linear)로 생각의 흐름을 이어감.

• 문제: Greedy/linear reasoning은 중간에 잘못된 단계가 나오면 되돌리기 어렵고, 탐색 공간을 충분히 활용하지 못함

해결책: Tree-of-Thoughts (ToT)

• 핵심: Reasoning을 tree 구조로 확장

  → 다양한 thought candidates를 분기(branch)시켜 탐색

2. Background

Notation:

• Pretrained LM: \(p_\theta\)
• 입력 \(x\), 출력 \(y\)

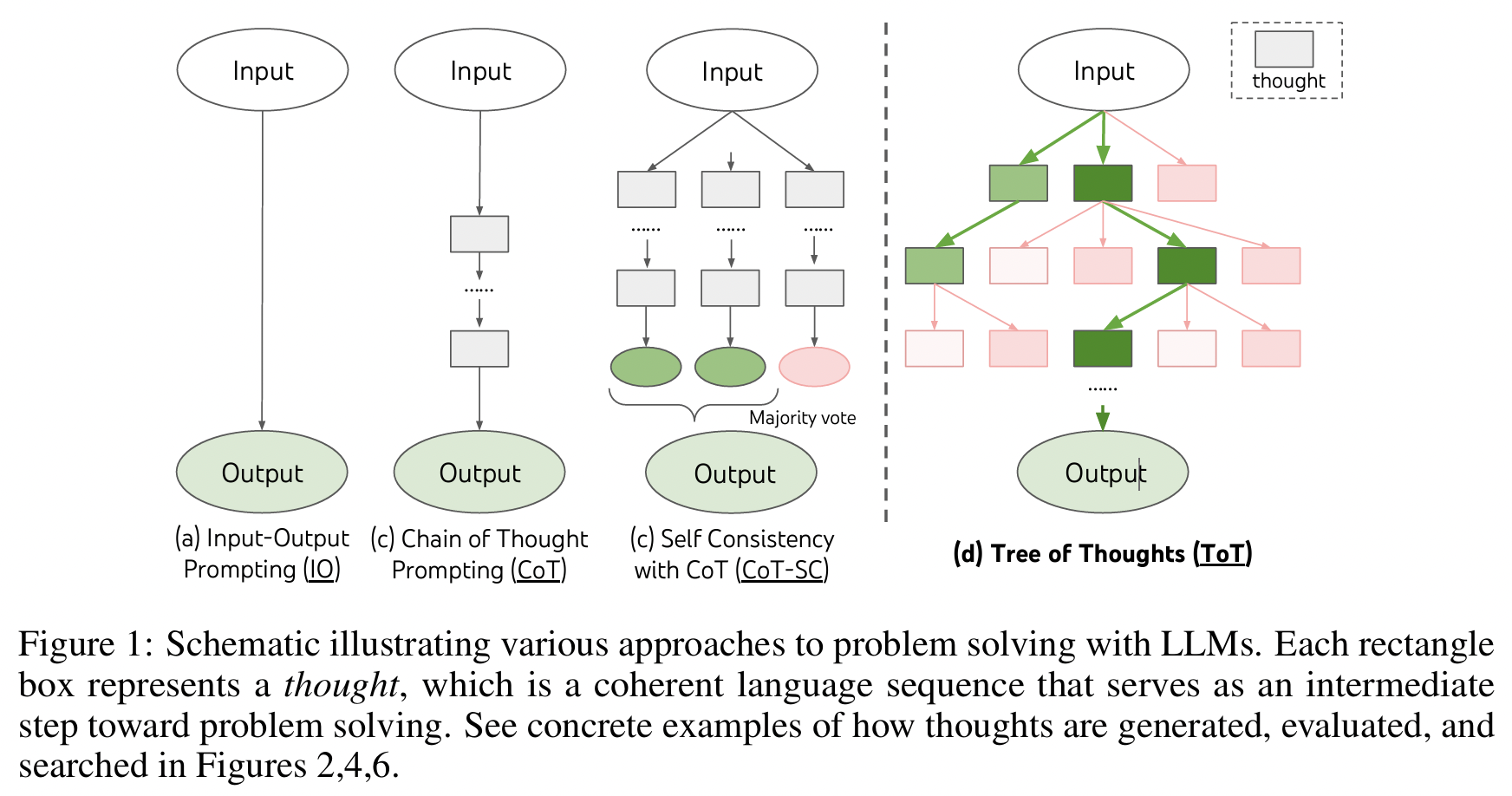
Prompting

• IO prompting:
  • \[y \sim p_\theta(y\mid \text{prompt}_{IO}(x))\]
  • 가장 단순한 입출력 방식
• Chain-of-Thought (CoT):
  • 중간 추론 조각 \(z_i\)를 순차 생성해 최종 답에 도달.
  • \([z_{1\ldots n}, y] \sim p_\theta^{\text{CoT}}(\cdot \mid x)\).
• Self-Consistency (CoT-SC):
  • CoT 경로를 k개 i.i.d. 샘플링 후 다수결로 최종 답 선택
  • 한 경로 안에서의 국소 탐색이 없고, 출력공간이 넓을 때는 다수결의 한계 O

3. Review: Self-Consistency (CoT-SC)

(1) CoT-SC 방식이란?

Procedure

• Step 1) 여러 개의 CoT 추론 경로를 독립적으로 샘플링합니다.
• Step 2) 마지막 정답을 다수결로 뽑음

Example) (Q) 1,2,3,4 조합해서 8 만들기

• 경로 A: “1+2=3, 3+4=7 → 답=7”
• 경로 B: “2+2=4, 4+4=8 → 답=8”
• 경로 C: “3+3=6, 6+4=10 → 답=10 ✅”

→ 정답은 C에 있지만, 다수결은 7이나 8을 뽑아버릴 수 있음.

(2) 한계점

“한 경로 안에서 국소 탐색(local search)이 없다”**

• CoT-SC는 (경로를 여러 개 뽑기는 하지만) 경로 내부에서 분기하거나 되돌아보며 탐색은 X

  \(\rightarrow\) 즉, 하나의 reasoning line이 잘못 가면 그대로 끝까지 잘못 가는 것

• 그래서 이 방식은 경로 내부(local level)에서 오류 수정이나 backtracking이 불가능

“출력공간이 넓을 때 다수결의 한계”

• 만약 가능한 정답 후보가 (1개가 아니라) 다양한 경우 (= 출력 공간이 넓다)

• 정답이 소수 branch에서만 나오는 경우라면, 다수결은 쉽게 틀릴 수 있음

3. Tree-of-Thoughts

ToT는 문제를 Tree 탐색 문제로 재정의

3.1 문제의식과 상태 정의

• 사람은 부분해(Partial solution) 들을 잇는 Tree를 휴리스틱으로 탐색
• 기존 LLM 추론의 두 한계
  1. 로컬: 한 단계(thought) 안에서 여러 분기를 탐색하지 않음
  2. 글로벌: 계획, lookahead, backtracking이 없음
• ToT의 상태(state): \(s = [x, z_{1\ldots i}]\).
  • (1) 입력 \(x\)
  • (2) 지금까지의 thought 시퀀스 \(z_{1\ldots i}\)로 구성된 부분해 노드.

3.2 ToT를 구성하는 4가지 질문

1. Thought Decomposition
2. Thought Generator
3. State Evaluator
4. Search Algorithm

(1) Thought Decomposition

Q) Thought 단위는?

• 한 thought \(z_i\)는 의미 있는 중간 단위(단어/구/문장/문단 등)여야
• 너무 작으면(토큰 단위) 평가가 어렵고
• 너무 크면(책 한 권) 다양 샘플링이 어려움

(2) Thought Generator \(G(p_\theta, s, k)\)

Q) 다음 thought 후보 \(k\)개를 어떻게 낼까?

(“현재 상태 s에서 다음에 전개할 생각 조각(thought) 후보 k개를 어떻게 뽑을까?”)

두 전략

• i.i.d. sampling from CoT prompt
• Sequential propose prompt

a) i.i.d. sampling from CoT prompt

아이디어: 같은 프롬프트(=현재 상태 \(s=[x, z_{1..i}]\))로부터 독립적으로 k번 샘플링

• \(z^{(j)} \sim p_\theta^{\text{CoT}}(z_{i+1}\mid x, z_{1..i}),\quad j=1..k\).

장점

• 병렬로 쉽게 뽑음.
• 후보 간 다양성(diversity) 을 크게 확보하고 싶을 때
  • (temperature/top-p 등을 조절해 다양성↑)

단점

• 출력 단위가 짧거나 제약적일 때(예: “다음 칸에 올 한 단어”), 중복 후보가 많이 나올 수 있음.

• 같은 맥락이라 상위 확률 후보가 반복적으로 뽑히는 mode collapse 위험.

예시

• 상태: 1–2문단까지 썼고, 3문단을 다양한 흐름으로 이어가고 싶을 때

• 프롬프트(요지): “다음 단락 후보를 1문단 분량으로 생성하라.”

• 샘플링: temperature=0.8, top-p=0.9로 5개 i.i.d. 샘플 →

  • \(z^{(1)}\): 주인공이 과거의 트라우마 회상
  • \(z^{(2)}\): 조력자 등장으로 방향 전환
  • \(z^{(3)}\): 내적 독백 심화
  • \(z^{(4)}\): 외부 사건(정전) 발생
  • \(z^{(5)}\): 반전 사실 드러남

  → 각각을 state evaluator가 점수 매기고, 상위 후보만 다음 깊이로 전개(beam/best-first).

b) Sequential propose prompt

아이디어: 한 번의 forward에서 순서 있는 후보 묶음 [z^{(1)}, …, z^{(k)}]을 직접 나열하도록 LLM에 시킴

• (“중복 금지, 서로 다른 유형, 간결한 포맷” 등을 명시적으로 강제)

• \([z^{(1)},\ldots,z^{(k)}] \sim p_\theta^{\text{propose}}(z_{i+1}^{(1\ldots k)} \mid s)\).

장점

• thought가 짧고 제약적일 때 (한 단어/한 식/하나의 그리드 단서) 좋음
• 한 호출에서 다양하고 비중복 후보를 “리스트”로 뽑도록 유도
• 포맷/제약(길이, 품사, 사전 제약 등)을 프롬프트로 엄격히 통제 가능.

단점

• 한 호출에 많은 내용을 요구하니 맥락폭/토큰 비용이 커질 수 있음.
• 나열 순서 편향이 생길 수 있어 후속 평가 모듈이 중요.

Summary

항목	i.i.d. sampling	sequential propose
목적	자유도 큰 thought에서 다양성 확보	짧고 제약적 thought에서 비중복·커버리지 확보
호출 방식	k회 독립 샘플	1회 호출에 k개 후보 나열
중복 방지	약함(샘플링 편향)	강함(프롬프트로 강제)
제약/포맷 통제	비교적 약함	강함(번호, 길이, 품사, 사전 등)
예시	창작 문단, 전략 설명	24게임 한 수, 크로스워드 단어, 코드 한 줄

def gen_iid(model, state, k, **decoding):
    return [ model.sample_next_thought(state, **decoding) for _ in range(k) ]

def gen_propose(model, state, k):
    prompt = build_propose_prompt(state, k, rules=...)
    items = model.generate_list(prompt)  # "1) ... 2) ... 3) ..."
    return parse_numbered_items(items)[:k]

(3) State Evaluator \(V(p_\theta, S)\)

Q) 어떤 상태가 유망한가?

• 핵심 아이디어: LM 스스로가 상태의 장단을 숙고(deliberate)하여 휴리스틱처럼 점수화.

두 방식:

• (1) Independent value: 각 상태 s를 독립적으로 평가
  • \(V(s) \sim p_\theta^{\text{value}}(v \mid s)\).
  • (예: “이 상태에서 문제를 풀 수 있을 가능성(0–10)?”)
• (2) Pairwise / comparative: 상태들을 서로 비교해 랭킹/선택
  • \(p_\theta^{\text{vote}}(s^\star \mid \{s\in S\})\).
  • (예: “다음 중 가장 유망한 진행은?”)

(4) Search Algorithm

Q) Tree를 어떻게 탐색할까?

본문에서는 두 가지를 사용:

• (1) BFS with beam \(b\) (Algorithm 1): 각 깊이에서 상위 \(b\) 상태만 유지/전개.
  • 깊이가 얕고(\(T\le 3\)), 초반 pruning이 잘 먹히는 곳에서!
  • e.g., Game of 24, Creative Writing에 사용
• (2) DFS + pruning/backtracking (Algorithm 2): 가장 유망한 경로를 깊게 탐색하다가
  • 상태값이 임계 이하 (\(V(s)\le v_{\text{th}}\))면 서브Tree 가지치기
  • 해에 도달하거나 막히면 부모로 backtrack.
  • e.g., Mini Crosswords(깊은 탐색)

종료/기록: 깊이 \(t>T\) 도달 시 출력을 기록; 임계값 기반 pruning으로 탐색 효율 개선.

4. Experiments