Retrieval & Fine-Tuning for In-Context Tabular Models

Retrieval & Fine-Tuning for In-Context Tabular Models

Thomas, Valentin, et al. "Retrieval & fine-tuning for in-context tabular models." NeurIPS (2024)

arxiv: https://arxiv.org/pdf/2406.05207

Abstract

Tabular data + Transformer-based ICL

$\rightarrow$ Promising results on smaller & less complex datasets

$\rightarrow$ Limitation: Struggled to scale to larger & more complex ones

Proposal: LoCalPFN (locally-calibrated PFN)

Base model = TabPFN

Combination of (1) retrieval & (2) fine-tuning

• (1) Retrieval
  • Local subset of the data by collecting kNN
• (2) Fine-tuning (FT)
  • Task-specific FT with this retrieved set of neighbours in context

Experiments

• Extensive evaluation on 95 datasets curated by TabZilla from OpenML

1. Introduction

Challenges of Tabular DL

• Diversity & heterogeneity of tabular data
• Tree-based methods
  • More robust to the inherent challenges of tabular data

Recent works: TabPFN

• TabPFN = Tabular + ICL

• Trained using a “prior-fitting” procedure

  $\rightarrow$ Encapsulating the heterogeneity of tabular data

• Process entirely new datasets in a single forward pass w/o training / tuning

Limitation of TabPFN = Scaling issue

$\rightarrow$ Memory scales quadratically in the size of the context!

Proposal = LocalPFN

• (1) Retrieval
  • kNN of a given query point as the context for classification
• (2) Fine-tuning (FT)
  • FT end-to-end for each task
  • With an approximate neighbour scheme to facilitate backpropagation
• Experiments: 95-dataset benchmark from TabZilla

2. Improving Tabular ICL with Retrieval and Fine-Tuning

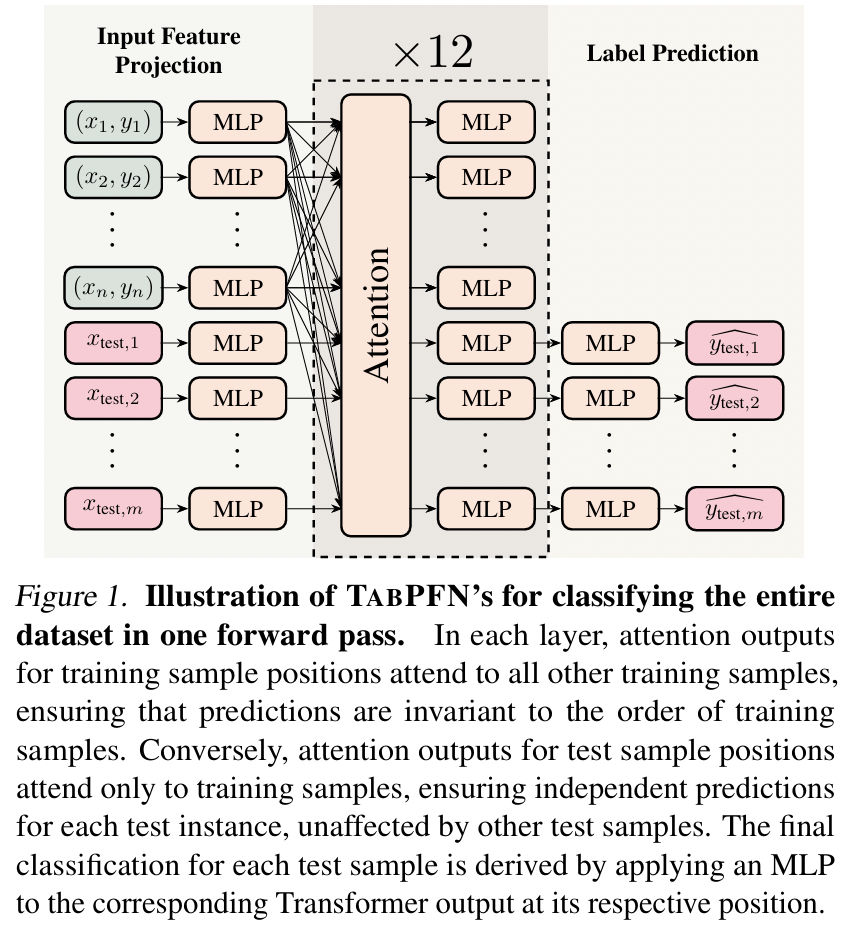
(1) Preliminaries on ICL for Tabular Data & TabPFN

LoCalPFN: Applies to ICL, specifically for classification tasks on tabular data

**TabPFN **

• Trained using a prior-fitting procedure
  • With a large number of synthetic datasets
• Trains an underlying transformer-based NN on various generative processes

Details of TabPFN

[Input] Entire training dataset + test dataset

• $\mathcal{D}{\text{train}} \triangleq \left{(x^{i}{\text{train}}, y^{i}{\text{train}})\right}{i=1}^{N}$.
  • Feature-label pairs $x^{i}{\text{train}} \in \mathbb{R}^D$ and $y^{i}{\text{train}} \in {1, \ldots, C}$
  • Query point $x_{\text{qy}}$ (potentially in a batch)

[Output] Distribution over labels $y_{\text{qy}} \in {1, \ldots, C}$.

Posterior predictive distribution

• $p_\theta(y_{\text{qy}} \mid x_{\text{qy}}, \mathcal{D}{\text{train}}) = \frac{\exp\left(f\theta(x_{\text{qy}}, \mathcal{D}{\text{train}})[y{\text{qy}}]\right)}{\sum_{c=1}^C \exp\left(f_\theta(x_{\text{qy}}, \mathcal{D}_{\text{train}})[c]\right)}$.

[ ]

where $[\cdot]$ denotes the vector indexing operation.

Contrary to classical machine learning methods which are trained on one dataset and then evaluated on the same distribution, TabPFN has been shown to be able to perform classification on a wide range of tasks without training, thanks to its diverse prior-fitting procedure. This makes it one of the rare foundation models for tabular data. Key to this is the ICL ability of TabPFN: by using various training examples as context, analogous to how transformers on language use the preceding tokens as context, TabPFN can classify new query points in a single forward pass.