Patch-Mix Contrastive Learning with Audio Spectrogram Transformer on Respiratory Sound Classification

Patch-Mix Contrastive Learning with Audio Spectrogram Transformer on Respiratory Sound Classification (Interspeech, 2023)

https://arxiv.org/pdf/2305.14032.pdf

Contents

1. Abstract
2. Related Works

   1. Respiratory Sound Classification

   2. Mixed Representation Learning

3. Methods
   1. Audio Spectrogram Transformer (AST)
   2. Patch-level CutMix on AST
   3. Patch-mix CL

Abstract

• Patch-mix augmentation = randomly mixes patches between different samples
• Model = with Audio Spectrogram Transformer (AST).

• Patch-Mix Contrastive Learning = distinguish the mixed representations in the latent space.

• Dataset: ICBHI dataset

1. Related Works

(1) Respiratory Sound Classification

ICBHI 2017

• several NN based methods for the lung sound classification task
  • mostly use CNN based
• Promising results by utilizing pretrained models on ImageNet [8, 9, 14] or AudioSet [15]

This paper..

• leverages the innovative AST model
• attains SOTA performance on the ICBHI lung sound dataset

(2) Mixed Representation Learning

Mixing different samples!

• Mixup [21], CutMix [22] : is a popular augmentation technique that has been applied regardless of the modality.
• Token-level CutMix methods combined with self-attention visual models have been proposed
  • TokenMix [28] : assigns the target score based on the content-based activation maps of two images
  • TokenMixup [29] : proposes Mixup with guided attention on the Transformer architectures.

• https://miro.medium.com/v2/resize:fit:1400/1*IR3uTsclxKdzKIXDlTiVgg.png

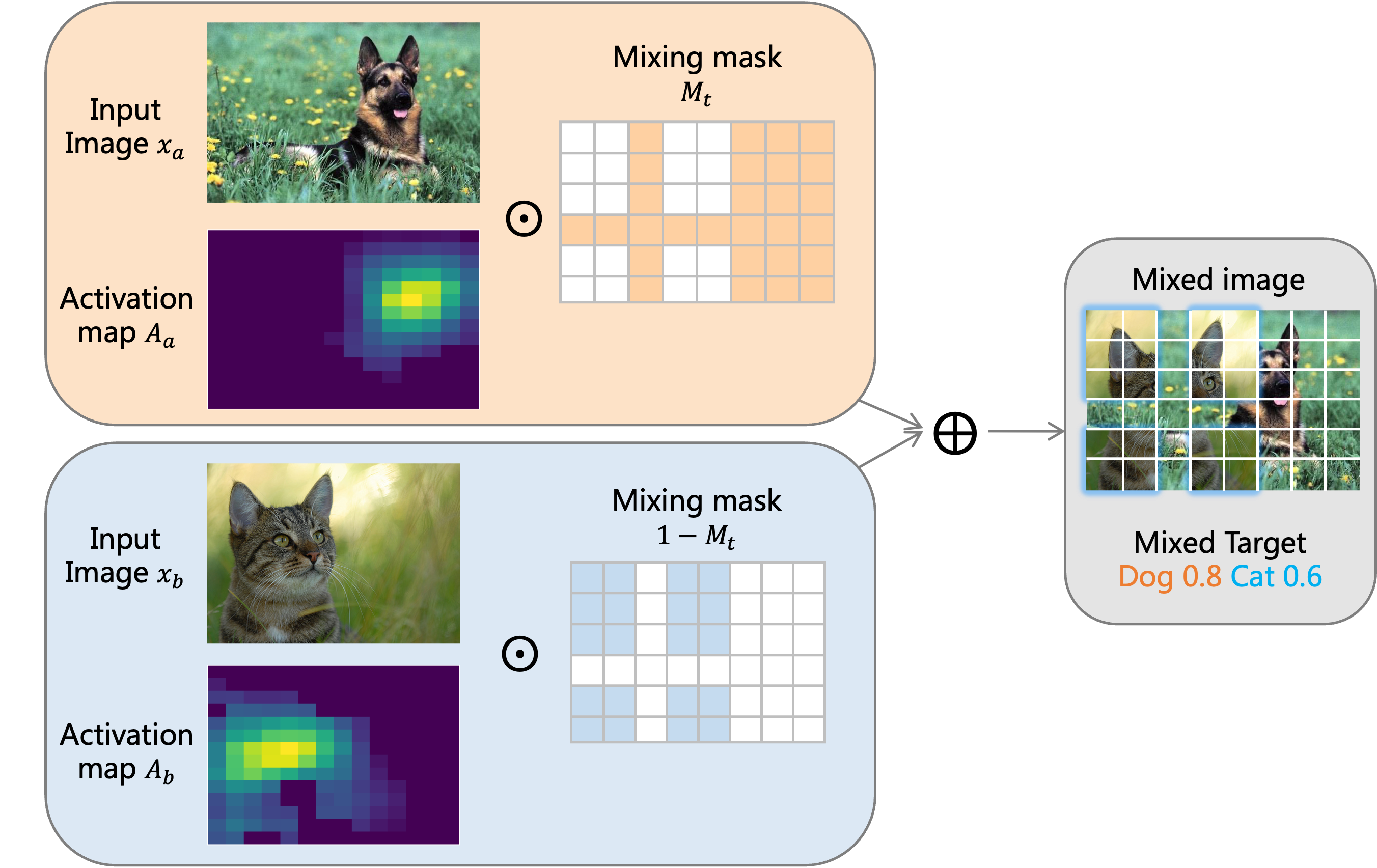
• https://raw.githubusercontent.com/sense-x/tokenmix/master/assets/tokenmix.png

• https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.researchgate.net%2Ffigure%2FTokenMix-and-CutMix-TokenMix-not-only-mixes-images-at-token-level-to-encourage-better_fig1_362089067&psig=AOvVaw2p3MN2lOw9msKoZR-12pQy&ust=1699164000607000&source=images&cd=vfe&opi=89978449&ved=0CBEQjRxqFwoTCLi_wafVqYIDFQAAAAAdAAAAABAU

This paper

• introduce a straightforward Patch-Mix technique
  • replaces randomly selected patches with those from other samples without any complex operation.
• further formulate a mixed contrastive loss

2. Methods

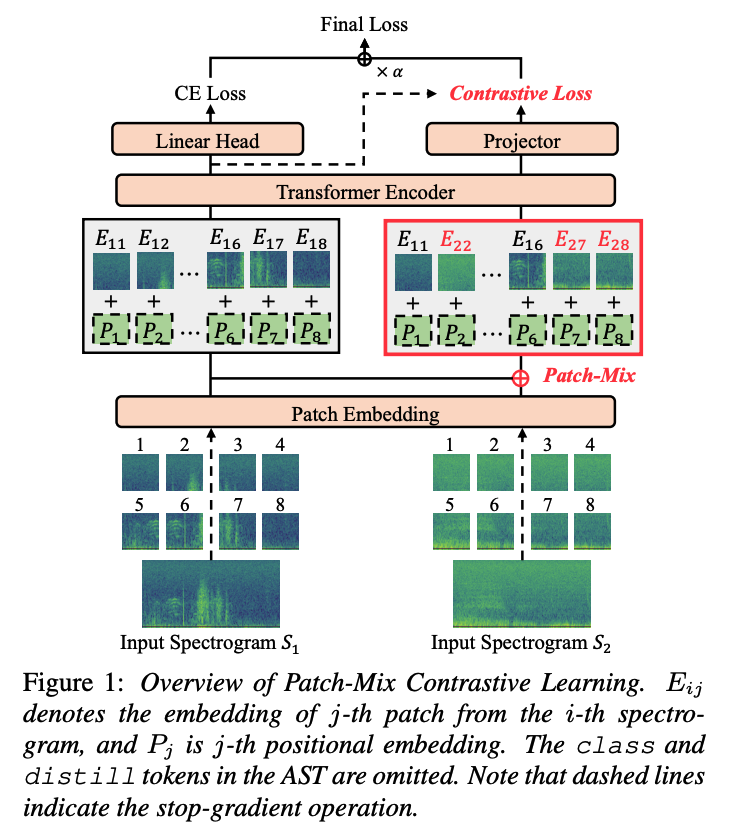
(1) Audio Spectrogram Transformer (AST)

• patchify spectrogram!

(2) Patch-level CutMix on AST

Mixup [21] and Cutmix [22]

• popular plug-and-play techniques

Transformer-based models

• split inputs into a sequence of patches (or tokens)

\(\rightarrow\) Recent works have utilized mixing techniques at the patch-level!

Propose an augmentation technique called Patch-Mix

Patch-Mix

• simply mixes patch embeddings with those from randomly chosen instances

• does not rely on complex operations such as neural activation maps

• adopt the same loss form as Mixup or CutMix

  ( = generating the label of CE loss based on the mixing ratio )

Two augmentation types of Patch-Mix:

• (1) Random selection of masks (“Patch” in Table 2)
• (2) Masking among the patch groups belonging to the same time domain to mimic Cutmix in raw audio signals (“TPatch”).

\(\rightarrow\) However, both augmentations did not show the improvement compared to simple fine-tuning results.

Reason : label hierarchy in respiratory sounds

• Linear combinations of ground truth labels may be counterintuitive in that patients should be diagnosed to abnormal with even small amount of crackle or wheeze sounds.

  \(\rightarrow\) conventional mixed loss function using \(\lambda\) -interpolated labels may not be appropriate for respiratory sound datasets!

(3) Patch-mix CL

In order to obtain a suitable loss function…propose a PatchMix contrastive loss

• distinguishing the mixed information within the latent space

\(\mathcal{L}_{\mathrm{CL}}=-\frac{1}{\mid I\mid } \sum_{i \in I}\left[\left(\lambda \cdot\left(h\left(\tilde{z}_i\right)^{\top} z_i / \tau\right)+(1-\lambda) \cdot\left(h\left(\tilde{z}_i\right)^{\top} z_m / \tau\right)\right)\right. \left.-\log \sum_{j \in I} \exp \left(h\left(\tilde{z}_i\right)^{\top} z_j / \tau\right)\right]\).

• \(z_i\) : encoder output of patch embedding \(E_i\)

• \(\tilde{z}_i\) : encoder output from mixed embedding with a ratio of \(\lambda\) between \(E_i\) and \(E_m\)

• \(h\) : projector that consists of two MLP layers with ReLU and BN layers

  ( all representation vectors are normalized before the dot product )

Final loss function : \(\mathcal{L}_{\mathrm{CE}}+\alpha \mathcal{L}_{\mathrm{CL}}\).