Liberty or Depth ; Deep BNN do not need complex weight posterior approximation ( NeurIPS 2020 )
Abstract
MFVI
- severely restrictive!
- BUT NOT in the case of DEEP newtorks!
prove that “deep mean-field variational weight posteriors” can induce similar distributions in function-space to those induced by shallower networks with complex weight posteriors
1. Introduction
VI in BNNs…ex) MFVI
MFVI : severe limitation ( \(\because\) correlations between weights )
But, not using MFVI…? too heavy computation
- ex) Structured covariance methods : bad time complexity
mean-field BNNs ( Wu et al. 2019 )
Argue that larger, deeper networks for mean-field approximation matters less!
- 1) simple parametric functions need complicated weight-distns to induce rich distns in function-space
- 2) complicated parametric functions can induce the same function-space distns with simple weight-ditsn
One way to have an expressive approximate posterior predictive
-
1) simple likelihood & rich approximate posterior over weights \(q(\theta)\)
-
2) simple \(q(\theta)\) & rich likelihood
( ex. deeper model mapping \(x\) to \(y\) )
2 hypothesis
-
1) Weight Distribution hypothesis
-
for BNN with full-cov weight distn,
there exists deeper BNN with “mean-field” weight distn
-
-
2) True Posterior hypothesis
-
for sufficiently deep & wide BNN
there exists mean-field distn over the weights of that BNN,
which induces the same distn over function values as that induced by posterior predictive
-
-
hypothesis 1) suggest that “shallow complex-covariance” = “deeper mean-field”
( show that Matrix Variate Gaussian distn is a special case of 3 layer product matrix distn )
( thus, allowing MFVI to model rich covariances )
-
hypothesis 2) states that mean-field weight distns can approximate the true predictive posterior
2. Related Work
(1) MacKay (1992)
- using MF approximation for Bayesian inference in NN is severe limitation
- “diagonal approximation” is no good, because of strong posterior correlations!
(2) Barber and Bishop (1998)
- “full-covariance VI”
- poor time complexity
(3) etc
-
structured-covariance approxximations…
( still have unattractive time complexity )
But there has been no work in DNN! (only shallow NN)
3. Emergence of Complex Covariance in Deep Linear Mean-Field Networks
1) Weight Distribution hypothesis is TRUE in linear networks
(1) Defining a Product matrix
- activation function of NN : \(\phi(\cdot)\)
- \(L\) weight matrices for a deep LINEAR model can be flattened ( called product matrix (\(M^{(L)}\)) )
- since the model is linear…
- there is one-to-one mapping
(2) Covariance of the Product matrix
-
derive an analytic form of covariance of the product matrix \(M^{(L)}\)
( this holds for ANY factorized weight distn with finite first & second order moment )
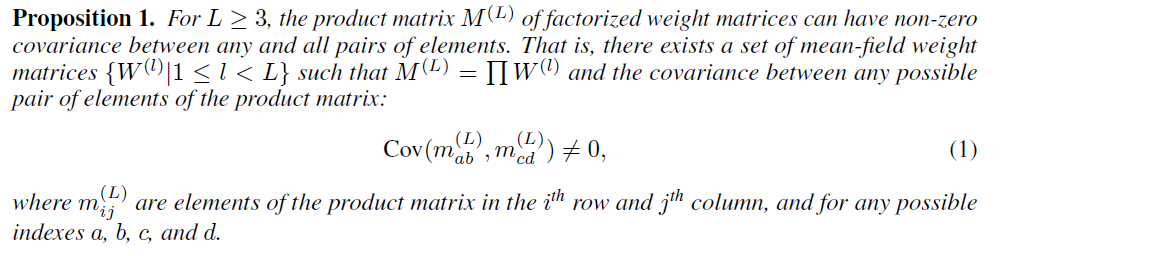
- shows that deep MF linear model is able to induce function-space distns which would require covariance between weights in a shallower model
(3) Numerical Simulation
- visualize the covariance between entries of the product matrix from a deep mean-field VI linear model
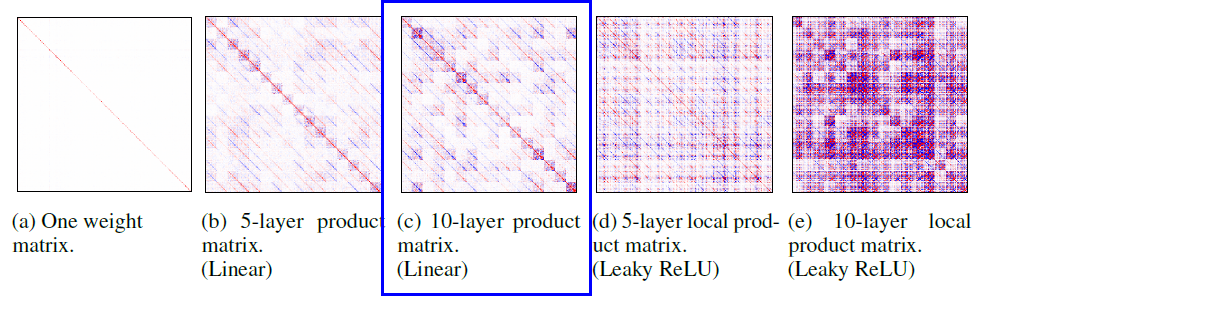
(4) How Expressive is the Product Matrix?
- MVG (Matrix Variate Gaussian) distn is a special case of the mean-field product matrix distn

4. Weight Dist Hypothesis in Deep Piecewise-Linear Mean Field BNNs
NN use non-linear activations
( these non-linearity make it impossible to consider product matrices :( )
Instead, show how to define local product matrix ( extension of product matrix )
- with piecewise-linear activation funcs
- ex) ReLUs, Leakly ReLUs
(1) Defining a Local Product Matrix
- NN with piecewise-linear activations induce piecewise-linear functions
- each region can be identified by a sign vector ( = switch on & off )
(2) Covariance of Local Product Matrix
-
given mean-field distn over weights of NN \(f\) with piecewise linear activations,
\(f\) can be written in terms of the local product matrix \(P_{x^{*}}\) within \(A\)

5. True Posterior Hypothesis in 2-hidden layer Mean-Field Networks
prove 2) True Posterior hypothesis using Universal Approximation Theorem (UAT)
- shows that BNN with mean-field approximate posterior with at leas 2 layers of hidden units can induce a function-space distribution that matches any true posterior distribution over function values arbitrarily closely.
