Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

Bijectors for NF

( 참고 : coursera : Probabilistic Deep Learning with Tensorflow2, Tensorflow official website )


Contents

  1. Bijector
  2. Scale bijectors and linear operator
  3. Transformed Distribution
  4. Subclassing Bijectors
  5. Training Bijector 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tfpl = tfp.layers


1. Bijector

tfb.Chain,tfb.Shift,tfb.Scale를 사용하여, 분포 \(z\)를 \(x\)로 변화시키기!

(a) make Bijector

example ) scale_n_shift Bijector를 다음과 같이 만든다.

scale=4.5
shift=7
scale_n_shift = tfb.Chain([tfb.Shift(shift),tfb.Scale(scale)])

####### 또 다른 방법 #############
scale_1 = tfb.Scale(scale)
shift_2 = tfb.Shift(shift)
scale_n_shift = shift_2(scale_1)


(b) Forward

\(z\)를 \(x\)로 transform한다 ( 다시 scaling해서 0으로 만듬을 확인할 수 있다 )

n=10000
z=normal.sample(n)

x = scale_n_shift(z)
tf.norm(x-(scale*z+shift))

<tf.Tensor: shape=(), dtype=float32, numpy=0.0>


(c) Inverse

forward & inverse를 통해원래대로 돌아옴을 확인할 수 있다

inv_x = scale_n_shift.inverse(x)
tf.norm(inv_x-z)


(d) Normalizing Flow

\[\log p_X(x) = \log p_Z(z) - \log \hspace{0.1ex}\left|\det J_f(z) \right|\] 
log_prob_x = normal.log_prob(z) - scale_n_shift.forward_log_det_jacobian(z,event_ndims=0)

# z = scale_n_shift.inverse(x) 이기 때문에, 아래와 같이 표현해도 무방하다.
log_prob_x2 = normal.log_prob(scale_n_shift.inverse(x)) + scale_n_shift.inverse_log_det_jacobian(x,event_ndims=0)


(e) example of Bijectors

다음과 같은 2개의 bijector에 대해 알아볼것이다.

  • 1) Softfloor bijector
  • 2) GumbelCDF bijector


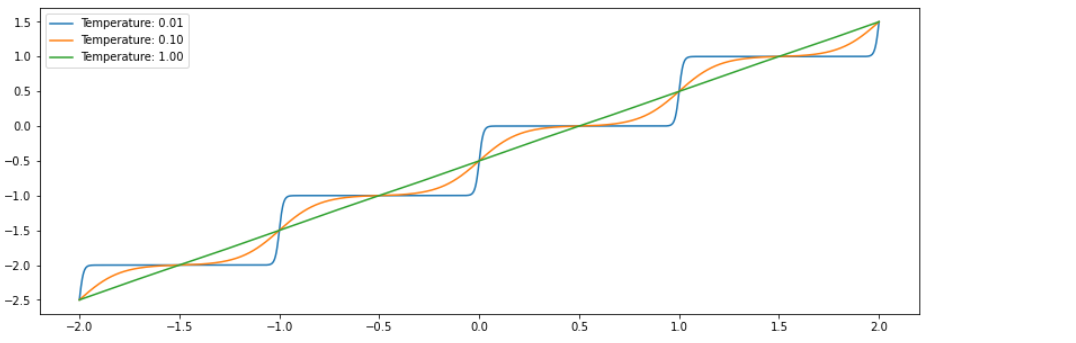
Softfloor bijector

  • compute a differentiable approximation to tf.math.floor(x)
  • softfloor(x, t) = a * sigmoid((x - 1.) / t) + b
    • a = 1 / (sigmoid(0.5 / t) - sigmoid(-0.5 / t))
    • b = -sigmoid(-0.5 / t) / (sigmoid(0.5 / t) - sigmoid(-0.5 / t))
x = tf.random.normal(shape=(100,1))
sf = tfb.Softfloor(temperature=[0.2,0.1])
y = sf.forward(x)  # shape : (100,2)

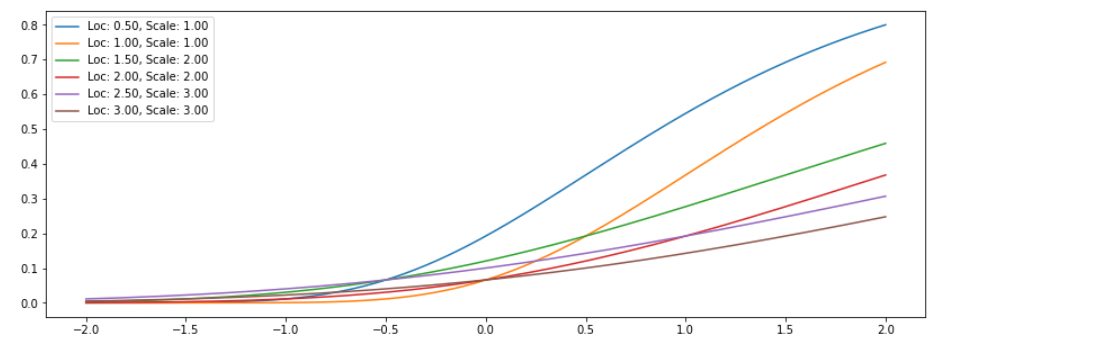
figure2


GumbelCDF bijector

  • \(F(x)=e^{-e^{(-x)}}\).
exps = tfb.GumbelCDF(loc=[0.5,1.0,1.5,2.0,2.5,3],scale=[1,1,2,2,3,3])

figure2


2. Scale bijectors and linear operator

Bijector는 위의 경우처럼 1차원 데이터에만 국한되지 않는다. 보다 고차원의 Bijector도 아래와 같이 생성할 수 있다.

  • ScaleMatvec

    • ScaleMatvecDiag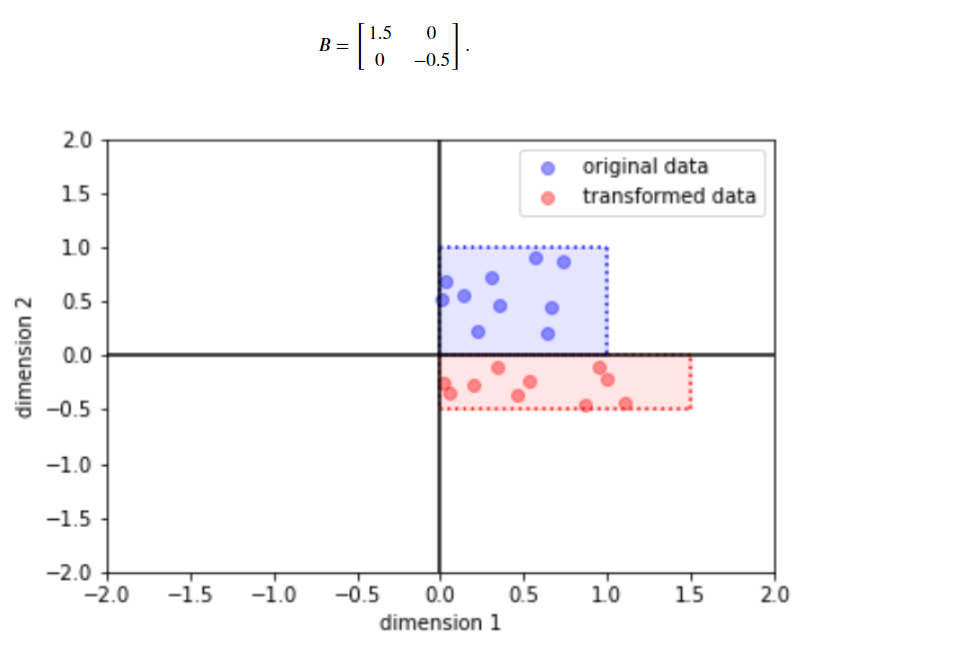

      figure2

    • ScaleMatvecTriL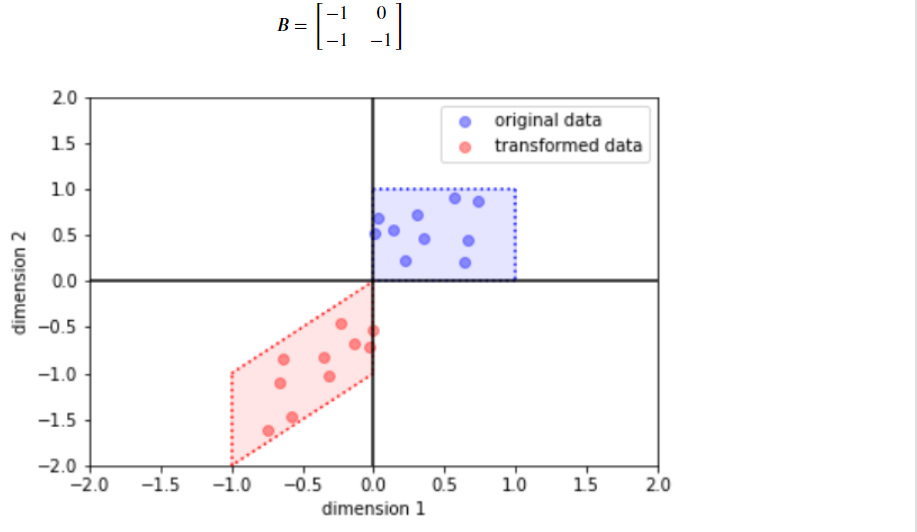

      figure2

  • ScaleMatvecLinearOperator

    • class : LinearOperatorDiag

      figure2

    • class : LinearOperatorFullMatrix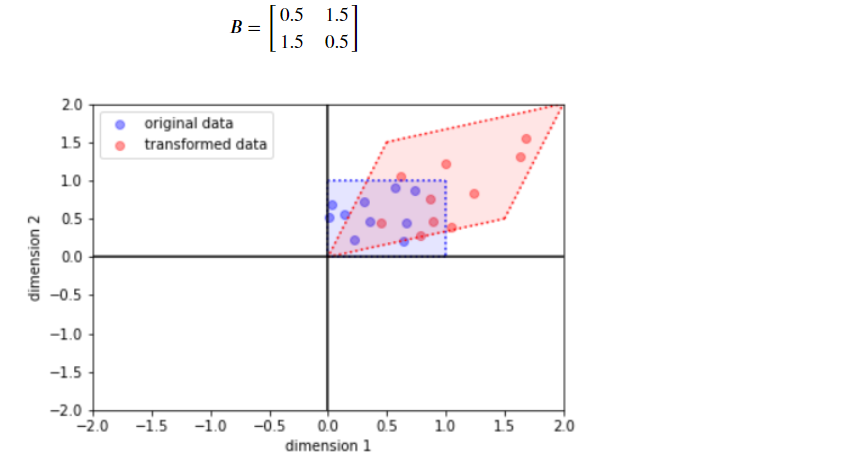

      figure2


2-1. ScaleMatvec

(a) ScaleMatvecDiag

bijector = tfb.ScaleMatvecDiag(scale_diag=[1.5, -0.5])
y = bijector(x)


(b) ScaleMatvecTriL

bijector = tfb.ScaleMatvecTriL(scale_tril=[[-1., 0.],
                                           [-1., -1.]])
y = bijector(x)


2-2. ScaleMatvecLinearOperator

( ScaleMatvec와는 다르게, LinearOperator를 통해 scale을 먼저 생성해주고, 이를 input으로 넣어야 한다. )

(a) LinearOperatorDiag

scale = tf.linalg.LinearOperatorDiag(diag=[1.5, -0.5])
bijector = tfb.ScaleMatvecLinearOperator(scale)
y = bijector(x)


(b) LinearOperatorFullMatrix

B = [[0.5, 1.5],
     [1.5, 0.5]]
scale = tf.linalg.LinearOperatorFullMatrix(matrix=B)
bijector = tfb.ScaleMatvecLinearOperator(scale)
y = bijector(x)


3. Transformed Distribution

A=tfd.TransformedDistribution(B,C)

  • A : Data distribution
  • B : Base distribution
  • C : Bijector
normal = tfd.Normal(loc=0.0,scale=1.0)

bijector1 = tfb.Exp()
bijector2 = tfb.ScaleMatvecTriL(scale_tril=[[1.0,0.0],[1.0,1.0]])
bijector3 = tfb.ScaleMatvecTriL(scale_tril=[[1.0,0.0],[1.0,1.0]])

log_normal = tfd.TransformedDistribution(normal,bijector1)
mvn = tfd.TransformedDistribution(normal,bijector2, event_shape=[2])
mvn2 = tfd.TransformedDistribution(normal,bijector3, batch_shape=[2],event_shape=[2])


Example

# (1) Base
normal = tfd.Normal(loc=0,scale=1)

# (2) Bijector
batch_shape=2
event_shape=4

tril = tf.random.normal((batch_shape,event_shape,event_shape))
scale_low_tri = tf.linalg.LinearOperatorLowerTriangular(tril)
scale_lin_op = tfb.ScaleMatvecLinearOperator(scale_low_tri)

# (3) Result
mvn = tfd.TransformedDistribution(normal,scale_lin_op,
                                 batch_shape=[batch_shape],event_shape=[event_shape])


Transformed 된 분포에서의 sample

n = 100
y = mvn.sample(sample_shape=(n,)) # shape : (100,batch_shape,event_shape)


4. Subclassing Bijectors

다음과 같은 Cubic Bijector를 만들어보자.

\(y=(ax+b)^3\). ( code : tf.squeeze(tf.pow(self.a*x + self.b,3)) )

다음의 함수는 반드시 들어가야 한다.

  • _forward
  • _inverse
  • _forward_log_det_jacobian
class Cubic(tfb.Bijector):
    def __init__(self, a, b, validate_args=False, name='Cubic'):
        self.a = tf.cast(a, tf.float32)
        self.b = tf.cast(b, tf.float32)
        if validate_args:
            assert tf.reduce_mean(tf.cast(tf.math.greater_equal(tf.abs(self.a), 1e-5), tf.float32)) == 1.0
            assert tf.reduce_mean(tf.cast(tf.math.greater_equal(tf.abs(self.b), 1e-5), tf.float32)) == 1.0
        super(Cubic, self).__init__(
            validate_args=validate_args, forward_min_event_ndims=0, name=name)
        
    def _forward(self,x):
        x = tf.cast(x,tf.float32)
        return tf.squeeze(tf.pow(self.a*x + self.b,3))
    
    def _inverse(self,y):
        y = tf.cast(y,tf.float32)
        return (tf.math.sign(y)*tf.pow(tf.abs(y),1/3)-self.b)/self.a
    
    def _forward_log_det_jacobian(self,x):
        x = tf.cast(x,tf.float32)
        return tf.math.log(3.*tf.abs(self.a))+2.*tf.math.log(tf.abs(self.a*x+self.b))



# example
cubic = Cubic([1.0,-2.0],[-1.0,0.4],validate_args=True)


4-1. Forward

cubic.forward(x) ( 혹은 그냥 cubic(x) )

x = np.linspace(-10,10,500).reshape(-1,1)
plt.plot(x,cubic.forward(x)) 
plt.show()

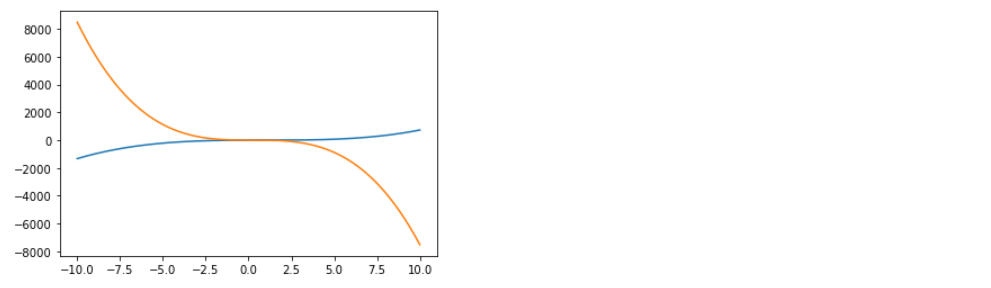
figure2


4-2. Inverse

cubic.inverse(x) ( 혹은 그냥 cubic(x) )

plt.plot(x,cubic.inverse(x))
plt.show()

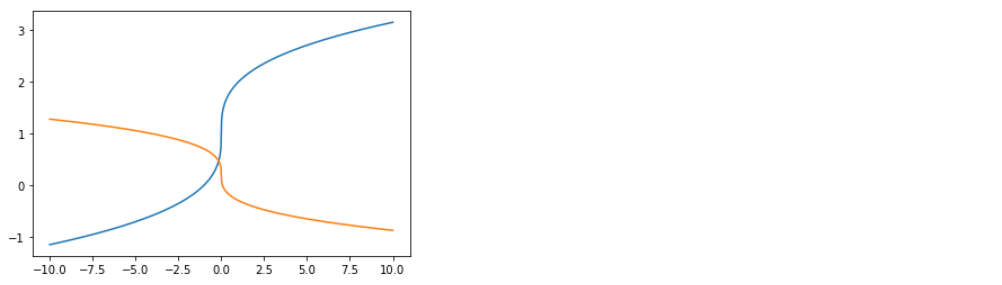
figure2


4-3. Log determinant

cubic.forward_log_det_jacobian(x,event_ndims)

plt.plot(x,cubic.forward_log_det_jacobian(x,event_ndims=0))
plt.show()

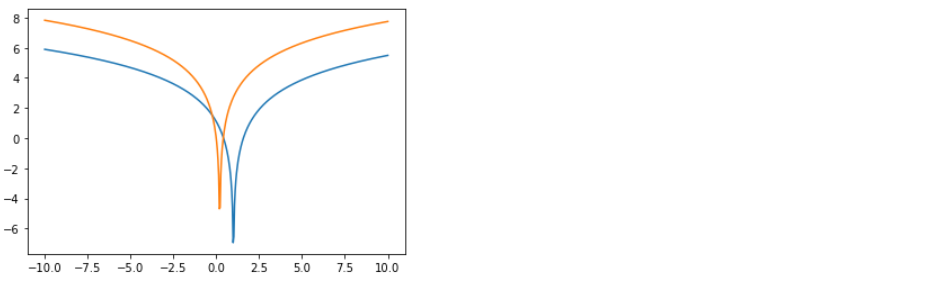
figure2


4-4. Transformed Distribution

위에서 만든 cubic bijector를 사용해서 base distribution (normal)을 변화시킨다

# (1) Base distn
normal = tfd.Normal(loc=0.,scale=1.)

# (2) Bijector
cubic = Cubic([1.0,-2.0],[-1.0,0.4],validate_args=True)

# (3) Transformed distn
cubed_normal= tfd.TransformedDistribution(normal,cubic,event_shape=[2])


tfb.Invert()를 통해 bijector의 inverse를 구할 수 있다.

( tfd.TransformedDistribution를 또 한번 사용할 필요가 없다 )

# (1) Base distn
normal = tfd.Normal(loc=0.,scale=1.)

# (2) Bijector
cubic = Cubic([1.0,-2.0],[-1.0,0.4],validate_args=True)
inverse_cubic = tfb.Invert(cubic)

# (3) Transformed distn
inv_cubed_normal= inverse_cubic(normal,event_shape=[2])


5. Training Bijector

Gaussian Mixture를 사례로, Bijector를 학습시켜볼 것이다.

( 즉, 얼마나 scaling되고 shift되는지 그 “정도”를 학습시키는 것이다 )


5-1. 가상의 정답 분포 생성

GMM with 2 components

  • \(\mu_1=2.3\) , \(\sigma_1 = 0.4\), ……\(w_1 = 0.45\)
  • \(\mu_2=-0.8\) , \(\sigma_2 = 0.4\) …….\(w_2 = 0.55\)
probs = [0.45,0.55]

mix_gauss = tfd.Mixture(
    cat=tfd.Categorical(probs=probs),
    components=[
        tfd.Normal(loc=2.3,scale=0.4),
        tfd.Normal(loc=-0.8,scale=0.4)
    ])


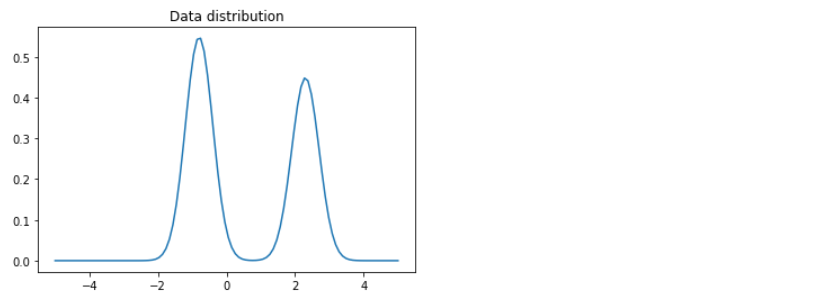
Visualization

x = np.linspace(-5.0,5.0,100)
plt.plot(x,mix_gauss.prob(x))
plt.title('Data distribution')
plt.show()

figure2


5-2. 학습 데이터셋 생성

Train data 10000개, validation data 1000개 생성 ( batch size = 128 )

x_train = mix_gauss.sample(10000)
x_train = tf.data.Dataset.from_tensor_slices(x_train)
x_train = x_train.batch(128)

x_valid = mix_gauss.sample(1000)
x_valid = tf.data.Dataset.from_tensor_slices(x_valid)
x_valid = x_valid.batch(128)


5-3. Trainable Bijector & Distribution 만들기

(1) Trainable Bijector 만들기

  • cubic의 parameter인 a와 b의 초기값으로, 각각 0.25와 -0.1을 주었다
trainable_inv_cubic = tfb.Invert(Cubic(tf.Variable(0.25),tf.Variable(-0.1)))


  • 이후에 학습이 이루어질 변수를 확인해보면…
trainable_inv_cubic.trainable_variables

(<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.25>,
 <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=-0.1>)


(2) Trainable Distribution 만들기

trainable_dist = tfd.TransformedDistribution(normal,trainable_inv_cubic)


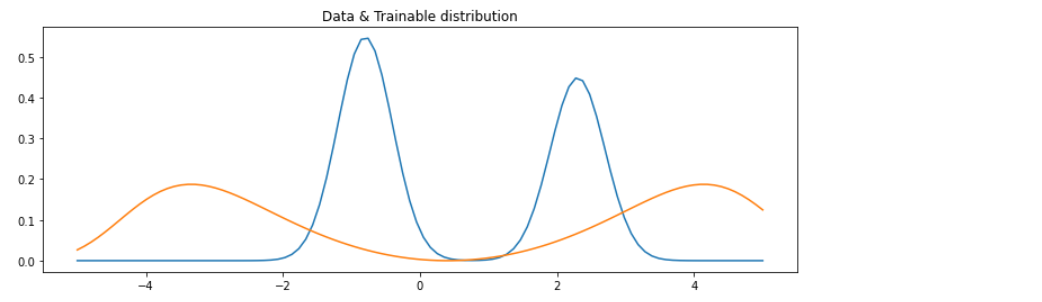
학습시키기 이전의 (초기값의) 분포

x = np.linspace(-5,5,100)
plt.figure(figsize=(12,4))
plt.plot(x,mix_gauss.prob(x),label='data')
plt.plot(x,trainable_dist.prob(x),label='trainable')
plt.title('Data & Trainable distribution')
plt.show()


5-4. Train

  • Optimizer : Adam

  • Loss : **Negative Log likelihood **

num_epochs = 10
opt = tf.keras.optimizers.Adam()
train_losses = []
valid_losses = []

for epoch in range(num_epochs):
    print("Epoch {}...".format(epoch))
    train_loss = tf.keras.metrics.Mean()
    val_loss = tf.keras.metrics.Mean()
    
    # Train
    for train_batch in x_train:
        with tf.GradientTape() as tape:
            tape.watch(trainable_inv_cubic.trainable_variables)
            loss = -trainable_dist.log_prob(train_batch)
        train_loss(loss)
        grads = tape.gradient(loss, trainable_inv_cubic.trainable_variables)
        opt.apply_gradients(zip(grads, trainable_inv_cubic.trainable_variables))
    train_losses.append(train_loss.result().numpy())
        
    # Validation
    for valid_batch in x_valid:
        loss = -trainable_dist.log_prob(valid_batch)
        val_loss(loss)
    valid_losses.append(val_loss.result().numpy())

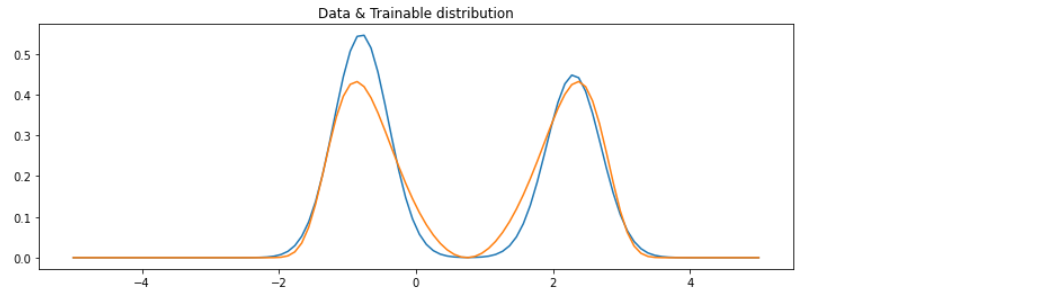
figure2


5-5. Result

실제 vs 예측 분포 비교하기

x = np.linspace(-5,5,100)
plt.figure(figsize=(12,4))
plt.plot(x,mix_gauss.prob(x),label='data')
plt.plot(x,trainable_dist.prob(x),label='trainable')
plt.title('Data & Trainable distribution')
plt.show()

figure2


학습된 파라미터는 다음과 같이해서 얻을 수 있다.

trainable_inv_cubic.trainable_variables

(<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.5768852>,
 <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=-0.4292613>)

You May Also Enjoy

less than 1 minute read

2 minute read

4 minute read

1 minute read