(paper 25) Self-Supervised Generalization with Meta Auxiliary Learning

Self-Supervised Generalization with Meta Auxiliary Learning

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Multi-task & Transfer Learning
   2. Auxiliary Learning
   3. Meta Learning
4. Meta Auxiliary Learning
   1. Problem Setup
   2. Model Objectives
   3. Mask SoftMax for Hierarchical Predictions
   4. The Collapsing Class Problem

0. Abstract

learning with auxiliary task \(\rightarrow\) Improve generalization ability of primary task

• but … cost of manually labeling auxiliary data

MAXL ( Meta AuXiliary Learning )

• automatically learns appropriate labels for auxiliary task
• train 2 NNs
  • (1) label-generarion network : to predict auxiliary labels
  • (2) multi-task network : to trian the primary task with auxiliary task

1. Introduction

Auxiliary Learning (AL) vs. Multi-task Learning (ML)

• AL : focus only on primary task
• MTL : focus on both primary task & auxiliary task

MAXL

• simple & general meta-learning algorithm

• defining a task = defining a label

  ( = optimal auxiliary task = one which has optimal labels )

  \(\rightarrow\) goal : automatically discover these auxiliary labels, using labels for primary task

2 NNs

1. Multi-task network
   • Trains primary task & auxiliary task
2. Label-generation network
   • learns the labels for auxiliary task

Key idea of MAXL

• use the performance of the primary task, to improve the auxiliary labels for the next iteration
• achieved by defining a loss for the label-generation network as a function of multi-task network’s performance on primary task training data

2. Related Work

(1) Multi-task & Transfer Learning

• MTL : shared representation & set of related learning tasks

• TL : to improve generatliaztion / incorporate knowledge from other domains

(2) Auxiliary Learning

Goal : focus only on single primary task

Can also perform auxiliary learning without GT labels ( = in unsupervised manner )

(3) Meta Learning

aims to induce the learning algorithm itself

MAXL : designd to learn to generate useful auxiliary labels, which themselves are used in another learning procedure

3. Meta Auxilary Learning

task : classification task ( both for primary & auxiliary task )

• auxiliary task : sub-class labelling problem
• ex) primary - auxiliary : Dog - Labrador

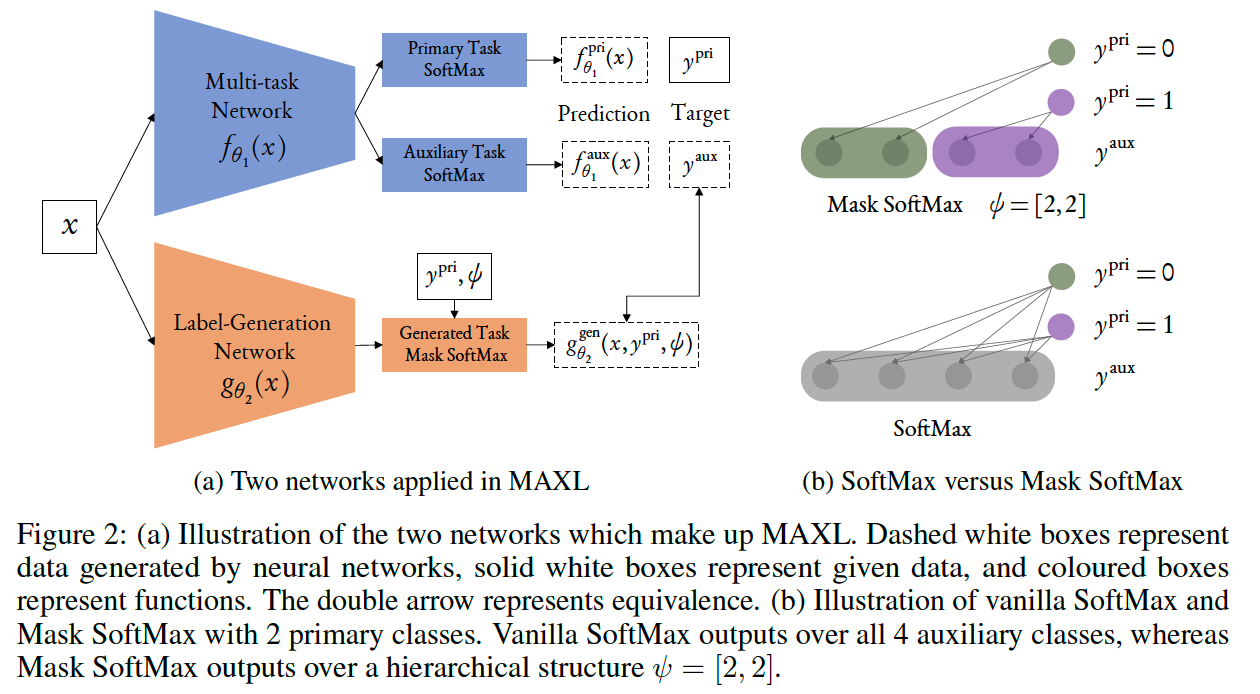
(1) Problem Setup

Notation

• \(f_{\theta_1}(x)\) : multi-task network
  • updated by loss of primary & auxiliary tasks
• \(g_{\theta_2}(x)\) : label-generation network
  • updated by loss of primary task

Multi-task Network

• apply hard parameter sharing approach

  ( common & task-specific parameters )

• notation

  • primary task prediction : \(f_{\theta_1}^{\text {pri }}(x)\)

    ( ground truth : \(y^{\text {pri }}\) )

  • auxiliary task prediction : \(f_{\theta_1}^{\text {aux }}(x)\)

    ( ground truth : \(y^{\text {aux }}\) )

Assign each primary class its own unique set of possibile auxiliary classes

( rather than sharing all auxiliary classes across all primary classes )

\(\rightarrow\) use hierarchical structure !!

Label-generation Network

• hierarchical structure \(\psi\)

  ( = determines the number of auxiliary classes for each primary class )

• output layer : masked SoftMax

  ( to ensure that each output node represents an auxiliary class, correspodning to only one primary class )

• Notation
  • input data : \(x\)
  • GT primary task label : \(y^{\text{pri}}\)
  • Auxiliary label : \(y^{\mathrm{aux}}=g_{\theta_2}^{\mathrm{gen}}\left(x, y^{\mathrm{pri}}, \psi\right)\)
• Allow soft assignment for generated auxiliary labels

(2) Model Objectives

2 stages per peoch

• stage 1) Train multi-task network
  • using primary task label & auxiliary labels
• stage 2) Train label-generation network

\(\rightarrow\) train both networks, in an iterative manner, until convergence

for both primary & auxiliary tasks, apply focal loss

• focusing parameter \(\gamma=2\)
• \(\mathcal{L}(\hat{y}, y)=-y(1-\hat{y})^\gamma \log (\hat{y})\),

[ Stage 1 ] Update parameters \(\theta_1\) for multi-task network

• \(\underset{\theta_1}{\arg \min }\left(\mathcal{L}\left(f_{\theta_1}^{\text {pri }}\left(x_{(i)}\right), y_{(i)}^{\text {pri }}\right)+\mathcal{L}\left(f_{\theta_1}^{\text {aux }}\left(x_{(i)}\right), y_{(i)}^{\text {aux }}\right)\right)\).
  • where \(y_{(i)}^{\text {aux }}=g_{\theta_2}^{\text {gen }}\left(x_{(i)}, y_{(i)}^{\text {pri }}, \psi\right)\)

[ Stage 2 ] Update parameters \(\theta_2\) for label-generation network

• leveraging the performance of the multi-task network to train the label-generation network can be considered as a form of meta learning

• \(\underset{\theta_2}{\arg \min } \mathcal{L}\left(f_{\theta_1^{+}}^{\text {pri }}\left(x_{(i)}\right), y_{(i)}^{\text {pri }}\right)\).

  • \(\theta_1^{+}\) : weights of the multi-task network after one gradient updates

    ( \(\theta_1^{+}=\theta_1-\alpha \nabla_{\theta_1}\left(\mathcal{L}\left(f_{\theta_1}^{\mathrm{pri}}\left(x_{(i)}\right), y_{(i)}^{\mathrm{pri}}\right)+\mathcal{L}\left(f_{\theta_1}^{\mathrm{aux}}\left(x_{(i)}\right), y_{(i)}^{\mathrm{aux}}\right)\right)\) )

problem : generated auxiliary labels can easily collapse

( = always generate the same auxiliary label )

\(\rightarrow\) solution : encourage the NN to learn more complex & informative auxiliary tasks, by applying entropy loss

• \(\theta_2 \leftarrow \theta_2-\beta \nabla_{\theta_2}\left(\mathcal{L}\left(f_{\theta_1^{+}}^{\text {pri }}\left(x_{(i)}\right), y_{(i)}^{\text {pri }}\right)+\lambda \mathcal{H}\left(y_{(i)}^{\text {aux }}\right)\right)\).

(3) Mask SoftMax for Hierarchical Predictions

• include a hierarchy \(\psi\)

• to implement this, design Mask Softmax

  ( to predict auxiliary labels only for certain auxiliary classes )

• \(M=\mathcal{B}(y, \psi)\).

• ex) primary task with 2 classes \(y=0,1\), and a hierarchy of \(\psi=[2,2]\)

  • binary masks :
    • \(M=[1,1,0,0]\) for \(y=0\)
    • \(M = [0,0,1,1]\) for \(y=1\)

Softmax vs Mask Softmax :

• Softmax : \(p\left(\hat{y}_i\right)=\frac{\exp \hat{y}_i}{\sum_i \exp \hat{y}_i}, \quad\)
• Mask Softmax : \(p\left(\hat{y}_i\right)=\frac{\exp M \odot \hat{y}_i}{\sum_i \exp M \odot \hat{y}_i}\)

(4) The Collapsing Class Problem

• introduce an additional regularization loss
• Entropy loss : calculates the KL divergence between…
  • (1) predicted auixliary label space \(\hat{y_{(i)}}\)
  • (2) uniform distribution \(\mathcal{U}\) for each \(i^{\text{th}}\) batch
• \(\mathcal{H}\left(\hat{y}_{(i)}\right)=\sum_{k=1}^K \hat{y}_{(i)}^k \log \hat{y}_{(i)}^k, \quad \hat{y}_{(i)}^k=\frac{1}{N} \sum_{n=1}^N \hat{y}_{(i)}^k[n]\).
  • \(k\) : total number of auxiliary classes
  • \(N\) : training batch size