(paper 26) Unsupervised Pre-training of Image Features on Non-Curated Data

Unsupervised Pre-training of Image Features on Non-Curated Data

Contents

1. Abstract
2. Introduction
3. Related Work
4. Preliminaries
   1. Self-supervision
   2. Deep Clustering
5. Method
   1. Combining self-supervision & clustering
   2. Scaling up to large number of targets

0. Abstract

most recent efforts : done on highly curated datasets ( ex. ImageNet )

\(\rightarrow\) this paper bridges the performance gap between curated data & massive raw datasets

1. Introduction

aim at learning good visual representations from unlabeled & non-curated datasets

\(\rightarrow\) YFCC100M dataset

• unbalanced
• long-tail distn of hashtags

Training on large-scale non-curated data requires…

• (1) model complexity to increase with data size
• (2) model stability to data distn changes

2. Related Work

Self Supervision

• pretext task
• encourage representations to be invariant/discriminative to particular types of input transformations

Deep Clustering

this paper builds upon the work, where k-means is used to cluster the visual representations

Learning on non-curated datsets

typically use metadata ( ex. hashtags, geolocalization )

3. Preliminaries

Notation

• \(f_\theta\) : feature-extracting function

  ( goal : learn a good mapping = produces general-purpose visual features )

(1) Self-supervision

• pretext task : extract target labels directly from data

  ( = make pseudo-labels \(y_n\) )

• given pseudo-labels, learn \(\theta\) jointly with linear classifier \(V\)

  \(\rightarrow\) \(\min _{\theta, V} \frac{1}{N} \sum_{n=1}^N \ell\left(y_n, V f_\theta\left(x_n\right)\right)\).

Rotation as self-supervision

RotNet … predict {0, 90, 180, 270} rotation degree

(2) Deep Clustering

Clustering based approaches for DNN

• build target classes by clustering features extracted by convnets

  ( targets are being updated )

• Notation

  • \(z_n\) : latent pseudo-label
  • \(W\) linear classifier

• alternate between…

  • (1) learning \(\theta\) & \(W\)
  • (2) updating pseudo-labels \(z_n\)

Loss function

• (1) optimize \(\theta\) & \(W\)
  • \(\min _{\theta, W} \frac{1}{N} \sum_{n=1}^N \ell\left(z_n, W f_\theta\left(x_n\right)\right)\).
  • labels \(z_n\) can be reassigned, by minimizing auxiliary loss function
• (2) update pseudo labels \(z_n\)
  • \(\min _{C \in \mathbb{R}^{d \times k}} \sum_{n=1}^N\left[\min _{z_n \in\{0,1\}^k \text { s.t. } z_n^{\top} 1=1} \mid \mid C z_n-f_\theta\left(x_n\right) \mid \mid _2^2\right]\).
    • \(C\) : matrix, where each column corresponds to a centroid
    • \(k\) : number of centroids
    • \(z_n\) : binary vector, with a single non-zero entry

Alternate optimization scheme

• problem ) prone to trivial solution
• solution ) re-assinging empty clusters & performing a batch-sampling based on an uniform distn over cluster assignments

4. Method

how to combine self-supervised learning & deep clustering

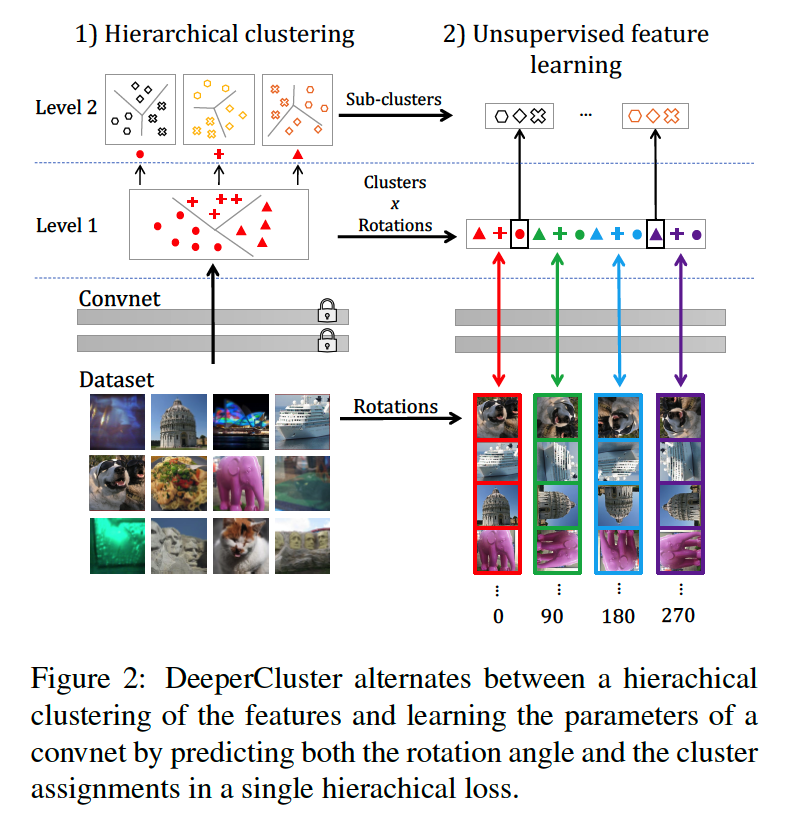
(1) Combining self-supervision & clustering

Notation

• Inputs : \(x_1, \ldots, x_N\) ( = rotated images )

• Targets : \(y_n\) ( = rotation angle )

  • \(\mathcal{Y}\) : set of possible rotation angles

• Cluster assignments : \(z_n\)

  ( changes during training )

  • \(\mathcal{Z}\) : set of possible cluster assignments

Way of combining self-supervision & clustering

• add the two losses ( defined above ) ?

  \(\rightarrow\) two independent tasks …. no interaction

• solution ) work with Cartesian product space : \(\mathcal{Y} \times \mathcal{Z}\)

  • capture richer interactions between 2 tasks
  • \(\min _{\theta, W} \frac{1}{N} \sum_{n=1}^N \ell\left(y_n \otimes z_n, W f_\theta\left(x_n\right)\right)\).

  \(\rightarrow\) still problem …… does not scale in the number of combined targest

  ( limits the use of a large number of cluster / self-supervised tasks )

  \(\rightarrow\) propose an approximation, based on scalable hierarchical loss

(2) Scaling up to large number of targets

Hierarchical Loss

• commonly used in LM ( predict a word out of large vocabulary )

Partition the target labels into 2-level hierarchy

• (1) predict a super-class
• (2) predict a sub-class

First level

• partition of images into \(S\) super-classes
• \(y_n\) : super-class assignment vector in \(\{0,1\}^S\)
  • ( 0, 0, 0, 1, 0, …. , 0 )

Second level

• parition within each super-class
• \(z_n^{s}\) : sub-class assignment vector in \(k_S\)
• there are \(S\) sub-class classifiers \(W_1, \cdots W_S\)

Jointly learn the parameters \((V, W_1, \cdots, W_S)\) & \(\theta\)

• loss function : \(\frac{1}{N} \sum_{n=1}^N\left[\ell\left(V f_\theta\left(x_n\right), y_n\right)+\sum_{s=1}^S y_{n s} \ell\left(W_s f_\theta\left(x_n\right), z_n^s\right)\right]\)

  ( where \(l\) is NLL )

Choice of super class

Natural choice :

• Super-classes : based on target labels from self-supervised tasks

• Sub-classes : labels produced by clustering

problem : does not take advantage of hierarchical structure to use bigger number of clusters

Proposal

• (1) Split the dataset into \(m\) sets ( with k-means ), on every \(T\) epoch
• (2) Use Cartesian product between the assignment to these \(m\) Clusters & angle rotation classes
  • form it as a super-classes ( \(4m\) super-classes )
• (3) These subsets are split with \(k\)-means with \(k\) Sub-classes