SCAN : Learning to Classify Images without Labels
Contents
- Abstract
- Introduction
- Method
- RL for semantic clustering
- A semantic clustering loss
- Fine-tuning through self-labeling
0. Abstract
Unsupervised Image Classification
-
automatically group images into semantically meaningful clusters, when GT labels are absent
-
previous works
- (1) end-to-end
- (2) two-step approach ( this paper )
- feature learning & clustering
1. Introduction
Representation Learning
-
use self-supervised learning to generate feature representations
( no need for label )
-
use pre-designed tasks, called pretext tasks
-
(1) two-stage approach
- representation learning : mainly used as the first pretraining stage
- ( second stage = fine-tuning on another task )
(2) end-to-end learning
- combine feature learning & clustering
Proposed work, SCAN
( SCAN = Semantic Clustering by Adopting Nearest neighbors )
- two-step approach
- Leverage the advantage of both
- (1) representation learning
- (2) end-to-end learning
Procedures of SCAN
-
step 1) learn feature representation via pretext task
-
(representation learning) use K-means
\(\rightarrow\) may have cluster degeneracy problem
-
(proposed) mine the nearest neighbors of each image, based on feature similarity
-
-
step 2) integrate semantically meaningful neighbors as prior intoa learnable approach
2. Method
(1) RL for semantic clustering
Notation
-
image dataset : \(\mathcal{D}=\left\{X_1, \ldots, X_{ \mid \mathcal{D} \mid }\right\}\)
-
class label ( absent ) : \(\mathcal{C}\)
\(\rightarrow\) However, we do not have access to class label !
Representation learning
- pretext task : \(\tau\)
- embedding function : \(\phi_{\theta}\)
- image & augmented image : \(X_i\) & \(T[X_i]\)
- minimize …
- \(\min _\theta d\left(\Phi_\theta\left(X_i\right), \Phi_\theta\left(T\left[X_i\right]\right)\right)\).
Conclusion : pretext tasks from RL can be used to obtain semantically meaningful features
(2) A semantic clustering loss
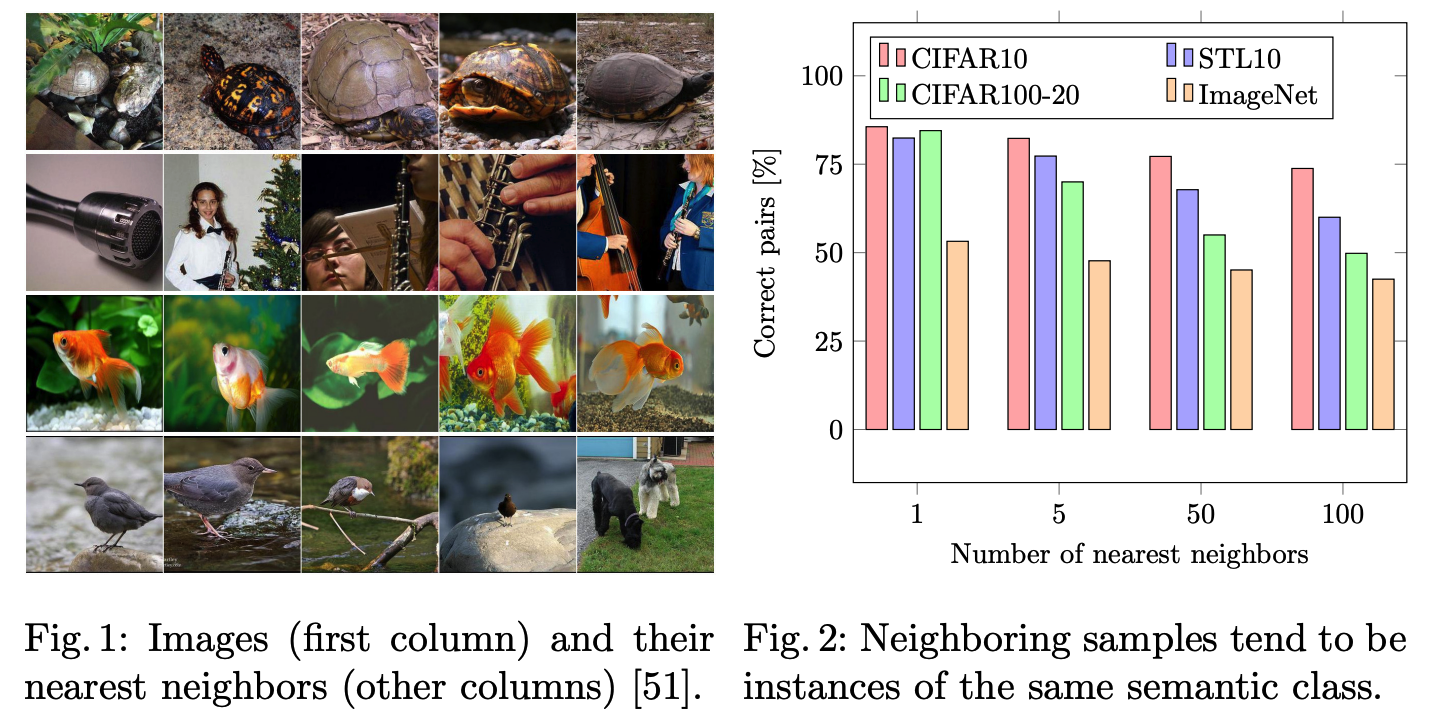
a) Mining nearest negibhors
naively applying K-means to obtained features \(\rightarrow\) lead to cluster degeneracy
[ Setting ]
-
Using pretext-tasks & nearest neighbors (NN) …….
for every sample \(X_i \in \mathcal{D}\), mine its \(K\) neareste neighbors, \(\mathcal{N}_{X_i}\)
Loss Function
Goal : learn a clustering function \(\Phi_\eta\)
- Classifies a sample \(X_i\) & \(\mathcal{N}_{X_i}\) together
- soft assignment over clusters \(\mathcal{C}=\{1, \ldots, C\}\), with \(\Phi_\eta\left(X_i\right) \in [0,1]^C\)
- probability of \(X_i\) assigned to \(c\) : \(\Phi_\eta^c\left(X_i\right)\)
Loss Function : \(\Lambda=-\frac{1}{ \mid \mathcal{D} \mid } \sum_{X \in \mathcal{D}} \sum_{k \in \mathcal{N}_X} \log \left\langle\Phi_\eta(X), \Phi_\eta(k)\right\rangle+\lambda \sum_{c \in \mathcal{C}} \Phi_\eta^{\prime c} \log \Phi_\eta^{\prime c}\)
-
with \(\Phi_\eta^{\prime c}=\frac{1}{ \mid \mathcal{D} \mid } \sum_{X \in \mathcal{D}} \Phi_\eta^c(X) .\)
-
(1st term) correct prediction
-
(2nd term) spreads the prediction across all clusters
( = can be replaced by KL-divergence )
(3) Fine-tuning through self-labeling
-
each sample is combined with \(K \geq 1\) Neighbors…but may have FP (False Positive)
-
experimently observed that samples with high confident predictions (\(p_{max}\approx1\) ) tend to have propor cluster
\(\rightarrow\) regard them as prototypes for each class

