(paper 36) Supervised Contrastive Learning

Supervised Contrastive Learning

Contents

1. Abstract
2. Introduction
3. Method
   1. Representation Learning Framework
   2. Contrastive Loss Functions

0. Abstract

Extend self-supervised batch contrastive approach to the fully-supervised setting

\(\rightarrow\) Allow us to effectively leverage label information

points of same class = pulled together

points of different classes = pushed apart

1. Introduction

propose a loss for supervised learning, that builds on the contrastive self-supervised literature

( normalized embeddings from the same class are pulled together )

Novelty

• consider many postives per anchor

  ( these positives are drawn from samples of the same class as the anchor, not form data augmentation )

• proposed loss function : SupCon

  • generalization of both triplet & N-pair loss
    • triplet : 1 pos & 1 neg
    • N-pair : 1 pos & N neg
  • simple to implement & stable to train

2. Method

Procedure

• step 1) given input data, apply data augmentation ( 2 copies per data)

• step 2) obtain 2048-dim normalized embedding
• step 3) compute supervised contrastive loss

(1) Representation Learning Framework

main components :

1. data augmentation module , \(A u g(\cdot)\)
   • \(\tilde{\boldsymbol{x}}=\operatorname{Aug}(\boldsymbol{x})\).
2. encoder network , \(\operatorname{Enc}(\cdot)\)
   • \(\boldsymbol{r}=\operatorname{Enc}(\boldsymbol{x}) \in \mathcal{R}^{D_E}\).
   • then, normalize to unit hyperspace
3. projection network , \(\operatorname{Proj}(\cdot)\)
   • \(\boldsymbol{z}=\operatorname{Proj}(\boldsymbol{r}) \in \mathcal{R}^{D_P}\).
   • Again normalize the output of this network

(2) Contrastive Loss Functions

for \(N\) randomly sampled sample&label pairs ( \(\left\{\boldsymbol{x}_k, \boldsymbol{y}_k\right\}_{\tilde{k}=1 \ldots N})\)

\(\rightarrow\) (data augmentation) \(\left\{\tilde{\boldsymbol{x}}_{\ell}, \tilde{\boldsymbol{y}}_{\ell}\right\}_{\ell=1 \ldots 2 N}\)

• \(\tilde{\boldsymbol{y}}_{2 k-1}=\tilde{\boldsymbol{y}}_{2 k}=\boldsymbol{y}_k\).

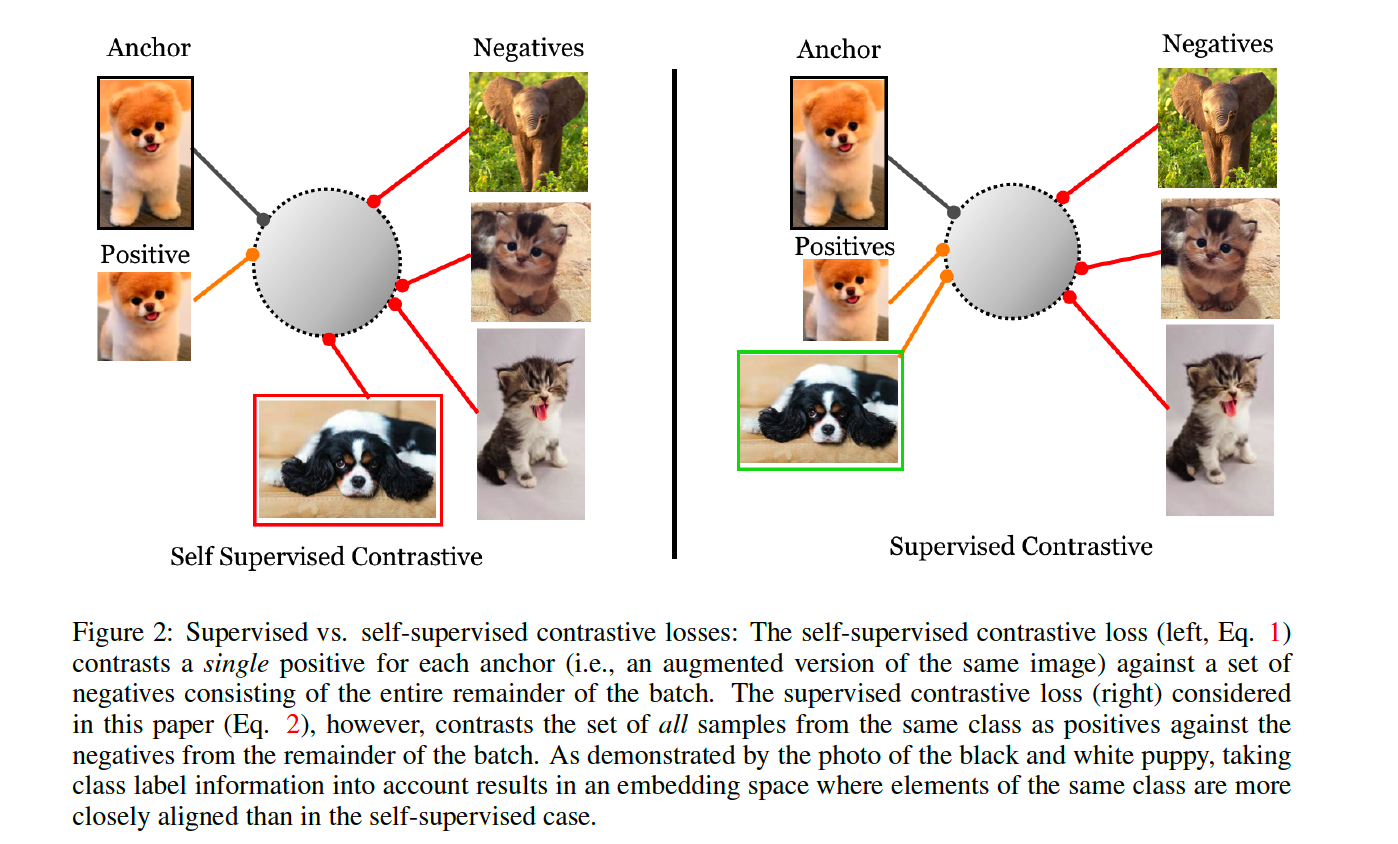
a) Self-Supervised Contrastive Loss

Notation

• \(i \in I \equiv\{1 \ldots 2 N\}\) : index of an arbitrary augmented sample
• \(j(i)\) : index of the other augmented sample ( from the same source sample )

Loss function : \(\mathcal{L}^{s e l f}=\sum_{i \in I} \mathcal{L}_i^{\text {self }}=-\sum_{i \in I} \log \frac{\exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_{j(i)} / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_a / \tau\right)}\)

( for general self-supervised contrastive learning )

• \(\boldsymbol{z}_{\ell}=\operatorname{Proj}\left(\operatorname{Enc}\left(\tilde{\boldsymbol{x}}_{\ell}\right)\right) \in \mathcal{R}^{D_P}\).
• \(A(i) \equiv I \backslash\{i\}\).
  • \(i\) : anchor
• positive & negative
  • positive : \(j(i)\)
  • negative : other \(2(N-1)\) indices \((\{k \in A(i) \backslash\{j(i)\})\)

b) Supervised Contrastive Losses

Above loss function ( = \(\mathcal{L}^{s e l f}=\sum_{i \in I} \mathcal{L}_i^{\text {self }}=-\sum_{i \in I} \log \frac{\exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_{j(i)} / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_a / \tau\right)}\) ) :

• incapable of using labeled data

Generalization : ( 2types )

• \(\mathcal{L}_{\text {out }}^{\text {sup }}=\sum_{i \in I} \mathcal{L}_{\text {out }, i}^{s u p}=\sum_{i \in I} \frac{-1}{ \mid P(i) \mid } \sum_{p \in P(i)} \log \frac{\exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_p / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_a / \tau\right)}\).
• \(\mathcal{L}_{\text {in }}^{\text {sup }}=\sum_{i \in I} \mathcal{L}_{i n, i}^{s u p}=\sum_{i \in I}-\log \left\{\frac{1}{ \mid P(i) \mid } \sum_{p \in P(i)} \frac{\exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_p / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_i \cdot \boldsymbol{z}_a / \tau\right)}\right\}\).

Both \(\mathcal{L}_{\text {out }}^{\text {sup }}\) & \(\mathcal{L}_{\text {in}}^{\text {sup }}\) Have desriable properties …

• (1) generalization to an arbitrary number of postivies

  • all positives in batch contribute to numerator

• (2) contrastive power increases with more negatives

• (3) intrinsic ability to perform hard pos/neg mining

  • gradient contributions from..

    • HARD pos/neg : large

    • EASY pos/neg : small