(paper 39) AugSelf

Improving Transferability of Representations via Augmentation-Aware Self-Supervision

Contents

1. Abstract
2. Auxiliary augmentation-aware self-supervision
   1. Summary
   2. Details

0. Abstract

Learning representations invariant to DA

\(\leftrightarrow\) However, might be harmful to certain downstream tasks

( if they rely on the characteristics of DA )

Solution : propose AugSelf

• optimize an auxiliariy self-supervised loss
• learns the difference of augmentation params

1. Auxiliary augmentation-aware self-supervision

(1) Summary

AugSelf

• by predicting the difference between 2 augmentation params \(\omega_1\) & \(\omega_2\)

• encourages self-supervised RL ( ex. SimCLR, SimSiam ) to preserve augmentation-aware information,

  that could be useful to downstream tasks

• negligible additional training cost

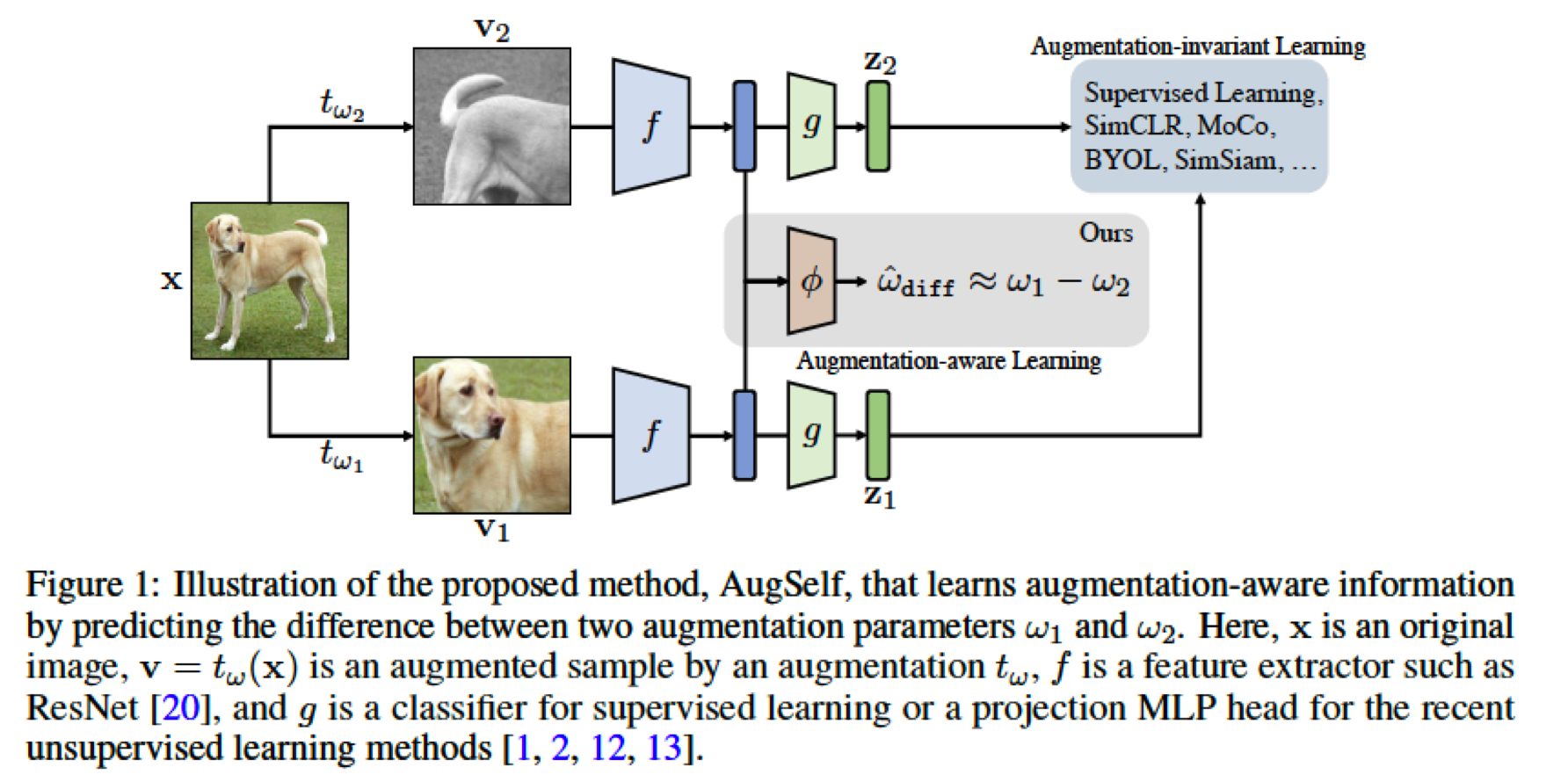
\(\rightarrow\) Add an auxiliary self-supervision loss, which learns to predict the difference between augmentation parameters of 2 randomly augmented views

(2) Details

Notation

• \(t_\omega\) : augmentation function
  • composed of different types of augmentations
  • augmentaiton parameter : \(\omega=\left(\omega^{\text {aug }}\right)_{\operatorname{aug} \in \mathcal{A}}\)
    • \(\mathcal{A}\) : the set of augmentations
    • \(\omega^{\text {aug }}\) : augmentation-specific parameter
• \(\mathbf{v}_1=t_{\omega_1}(\mathbf{x})\) and \(\mathbf{v}_2=t_{\omega_2}(\mathbf{x})\) : 2 randomly augmented views

Loss function :

• \(\mathcal{L}_{\text {AugSelf }}\left(\mathbf{x}, \omega_1, \omega_2 ; \theta\right)=\sum_{\text {aug } \in \mathcal{A}_{\text {Augself }}} \mathcal{L}_{\text {aug }}\left(\phi_\theta^{\text {aug }}\left(f_\theta\left(\mathbf{v}_1\right), f_\theta\left(\mathbf{v}_2\right)\right), \omega_{\text {diff }}^{\text {aug }}\right)\).
  • \(\mathcal{A}_{\text {Augself }} \subseteq \mathcal{A}\) : set of augmentations for augmentation-aware learning
  • \(\omega_{\text {diff }}^{\text {aug }}\) : difference between two augmentation-specific parameters \(\omega_1^{\text {aug }}\) and \(\omega_2^{\text {aug }}\)
  • \(\mathcal{L}_{\text {aug }}\) : augmentation specific loss

Easy to incorporate AugSelf into SOTA unsupervised learning methods

• with negligible additional training cost

ex) SimSiam + SelfAug

• loss function : \(\mathcal{L}_{\text {total }}\left(\mathbf{x}, \omega_1, \omega_2 ; \theta\right)=\mathcal{L}_{\text {SimSiam }}\left(\mathbf{x}, \omega_1, \omega_2 ; \theta\right)+\lambda \cdot \mathcal{L}_{\text {AugSelf }}\left(\mathbf{x}, \omega_1, \omega_2 ; \theta\right)\).

• Random Cropping : \(\omega_{\text {diff }}^{\text {crop }}=\omega_1^{\text {crop }}-\omega_2^{\text {crop }}\)
• Random Horizontal Flipping : \(\omega_{\text {diff }}^{\text {flip }}=\mathbb{1}\left[\omega_1^{\text {flip }}=\omega_2^{\text {flip }}\right]\)
• Color Jittering : \(\omega_{\text {diff }}^{\text {color }}=\omega_1^{\text {color }}-\omega_2^{\text {color }}\)
  • normalize all intensities into [0,1] …….. \(\omega^{\text {color }} \in[0,1]^4\)