SimMIM : a Simple Framework for Masked Image Modeling
Contents
- Abstract
- Introduction
- Approach
- MIM Framework
- Masking Strategy
- Prediction Head
- Prediction Targets
0. Abstract
propose SimMIM
-
a simple framework for masked image modeling
-
without the need for special designs
- ex) block-wise masking and tokenization via discrete VAE or clustering
[ study the major components in our framework ]
\(\rightarrow\) simple designs of each component !!
- (1) random masking ( with a moderately large masked patch size )
- (2) predicting RGB values of raw pixels ( by direct regression )
- (3) prediction head
performs no worse than complex designs
1. Introduction
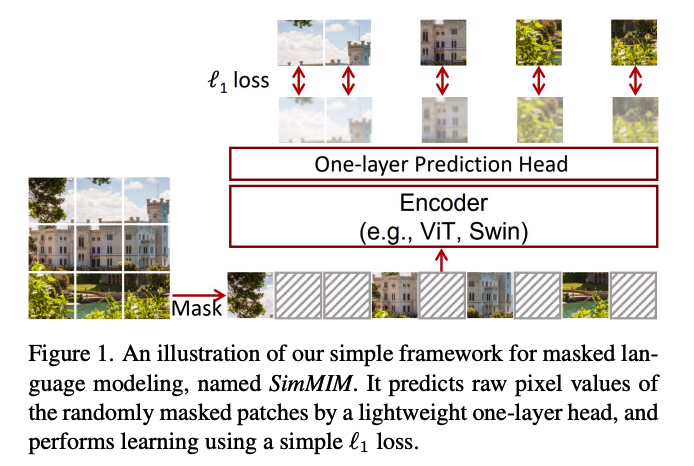
summary
-
random masking of input image patches,
-
using a linear layer to regress the raw pixel values of the masked area
-
with an \(l\)1 loss
2. Approach
(1) MIM Framework
SimMIM
-
learns representation through MIM
( = masks a portion of input & predict it )
-
4 major components
(a) Masking strategy
- a-1) how to select the area to mask
- a-2) how to implement masking
(b) Encoder architecture
-
extracts a latent feature for the masked image
( used to predict the original signals )
-
expected to be transferable to various vision task
(c) Prediction head
- applied on the latent feature for prediction
(d) Prediction target
- defines the form of original signals to predict.
- either be the…
- raw pixel values
- transformation of raw pixel values
- loss : CE loss, \(l_1\), \(l_2\) loss
(2) Masking Strategy
use a learnable mask token vector to replace each masked patch
- ex) Patch-aligned random masking (v)
- ex) Central region masking strategy
- ex) Complex block-wise masking strategy

(3) Prediction Head
show that the prediction head can be made extremely lightweight
(4) Prediction Targets
Raw pixel value regression
- pixel values are continuous
\(l_1\)-loss : \(L=\frac{1}{\Omega\left(\mathbf{x}_M\right)} \mid \mid \mathbf{y}_M-\mathbf{x}_M \mid \mid _1\)
- where \(\mathbf{x}, \mathbf{y} \in \mathbb{R}^{3 H W \times 1}\) are the input RGB values and the predicted values
- \(M\) : set of masked pixels
- \(\Omega(\cdot)\) : number of elements
