CORE: Self- and Semi-supervised Tabular Learning with COnditional Regularizations
Notation
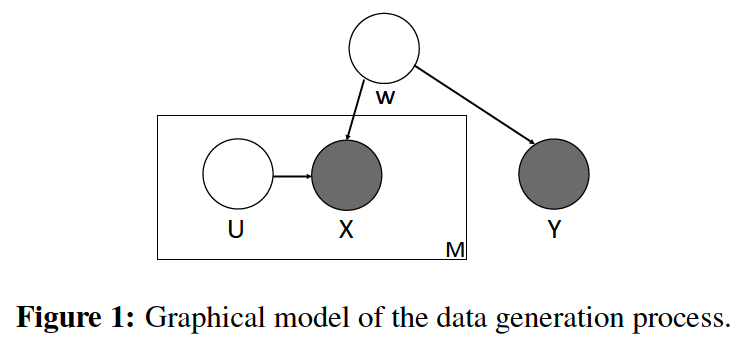
- generation of input : \(X \in \mathbb{R}^M\)
- outcome : \(Y \in \mathbb{R}\)
- low-dim signal : \(W \in \mathbb{R}^D\)
- drawn from \(p(W)\) …… where \(D<M\)
- individual noises : \(U^j\)
- drawn from \(p\left(U^j\right)\) …… for \(j=1, \cdots, M\)
Assumption
- input \(X^j\) ( = \(j\)-th dimension ) is generated from \(p\left(X^j \mid W, U^j\right)\) for \(j=1, \ldots, M\)
- outcome \(Y\) is generated from \(p(Y \mid W)\).
predicting \(Y\) requires estimation of \(W\)
& learning to infer \(W\) Is possible on unlabeled \(X\)
1. Self-supervised CORE
Setting : ENC & DEC from AE
Key ida : prevent ENC from memorizing \(X\)
Process : for a given input \(X\)….
-
step 1) create \(\hat{X}(j)\)
-
the \(j\)-th dimension replaced by samples from \(p\left(X^j \mid X^{-j}\right)\)
-
sampling from \(p\left(X^j \mid X^{-j}\right)\) …. requireS \(M\) different conditional distribution estimators?
\(\rightarrow\) no! use DDLK ( only need to generate one knockoff \(\tilde{X}\) )
-
- step 2) set \(\hat{X}(j)^j=\tilde{X}^j\) and \(\hat{X}(j)^{-j}=X^{-j}\)
- step 3) conditional regularization (CORE)
- \(\sum_{j=1}^M \mathbb{E}_{X, \hat{X}(j)} \mid \mid \operatorname{dec}(\operatorname{enc}(X))-\operatorname{dec}(\operatorname{enc}(\hat{X}(j))) \mid \mid _2^2\).
Encoder : if encoder memorizes \(X^{j}\) , CORE loss will be large!
- due to conditional resampling of the \(j\)-th dimension in \(\hat{X}(j)\)
Decoder : keep the decoder constant in the CORE loss
- do not take any gradient ( no gradient )
Loss function :
- \(\mathbb{E}_X \mid \mid \operatorname{dec}(\operatorname{enc}(X))-X \mid \mid _2^2+\alpha \cdot \sum_{j=1}^M \mathbb{E}_{X, \hat{X}(j)} \mid \mid n g(\operatorname{dec})(\operatorname{enc}(X))-n g(\operatorname{dec})(\operatorname{enc}(\hat{X}(j))) \mid \mid _2^2\).
2. Semi-supervised CORE
Notation :
- supervised loss \(l_{\text {sup }}\)
- consistency loss \(l_c\)
Loss function :
- \(\mathbb{E}_{X, Y} l_{\text {sup }}(f(\operatorname{enc}(X)), Y)+\beta \cdot \sum_{j=1}^M \mathbb{E}_{X, \hat{X}(j)} l_c(f(\operatorname{enc}(X)), f(\operatorname{enc}(\hat{X}(j))))\).
