(2) Convex Sets

2. Convex Sets

2-1. Affine & Convex Sets

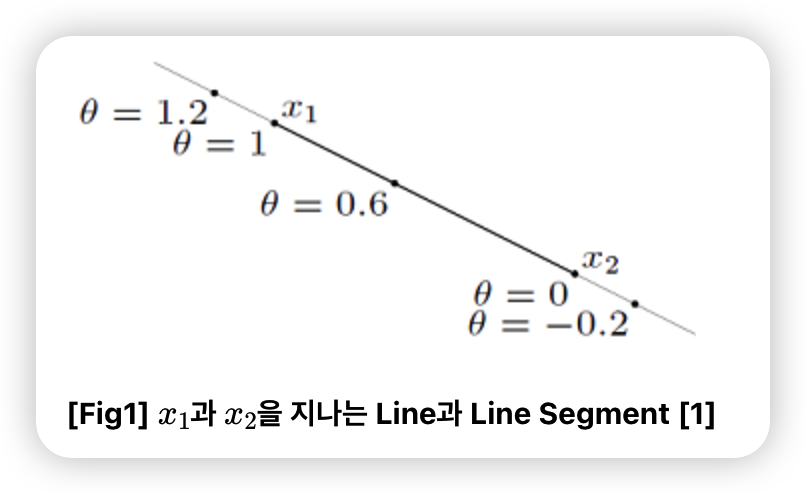
a) Line, Line Segment, Ray

\(y=\theta x_{1}+(1-\theta) x_{2}\) .

• Line (직선) : with \(\theta \in R\)
• Line Segment (선분) : with \(0 \leq \theta \leq 1\)
• Ray (반직선) : with \(\theta \geq 0\)

b) Affine Set

Affine Set

• \(\theta x_{1}+(1-\theta) x_{2} \in C\) with \(\theta \in R\) with \(\theta_{1}+\theta_{2}+\ldots+\theta_{k}=1\)
• 특징 : 계수의 합을 1로 제한. 양/음의 제한은 없음

Affine Combination

• \(\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{k} x_{k} \in C\) with \(\theta_{1}+\theta_{2}+\ldots+\theta_{k}=1\)
• 특징 : 계수의 합을 1로 제한. 양/음의 제한은 없음

Affine Hull

• aff \(C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \ldots, x_{k} \in C, \theta_{1}+\cdots+\theta_{k}=1\right\}\)
• affine combination들의 집합 ( 집함 \(C\)를 포함하는 가장 작은 affine set )

Affine Set & subspace와의 관계

• notation
  • \(C\) : affine set
  • \(x_0 \in C\).
  • \(V=C-x_0 =\{x-x_0 \mid x \in C\}\) : subspace
• Affine set \(C\)는, linear subspace \(V\)를 \(x_0\)만큼 translation 한 것
  • \(C=V+x_{0}=\left\{v+x_{0} \mid v \in V\right\}\).
  • \(C\) 의 차원 = \(V\) 의 차원 \(\left(C, V \subseteq \mathbb{R}^{n}\right)\)

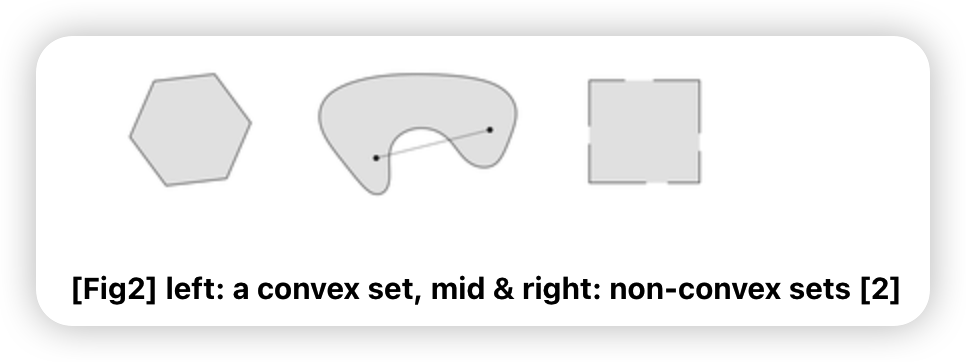
c) Convex Set

Convex Set

• \(\theta x_{1}+(1-\theta) x_{2} \in C\) with \(0 \leq \theta \leq 1\) & \(\theta_{1}+\theta_{2}+\ldots+\theta_{k}=1\)
• 특징 : 계수의 합을 1로 제한 + 양수 제한

Convex Combination

• \(\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{k} x_{k} \in C\) with \(\theta_{1}+\theta_{2}+\ldots+\theta_{k}=1\)
• 특징 : 계수의 합을 1로 제한 + 양수 제한

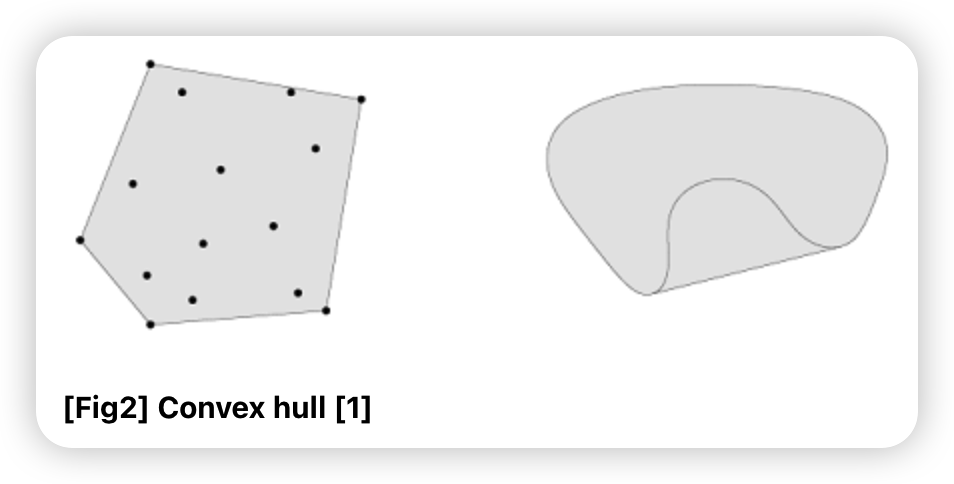
Convex Hull

• Cons \(C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \ldots, x_{k} \in C, \theta_{1}+\cdots+\theta_{k}=1, \theta_i >0 \right\}\)
• convex combination들의 집합 ( 집함 \(C\)를 포함하는 가장 작은 affine set )

d) Cone

Cone

• \(\theta x \in C\) with \(x \in C, \theta \geq 0\)

• 원점을 포함해야!

• 원점에서 시작해서, \(x \in C\)를 지나는 Ray를 만들었을 때,

  \(\theta \in C\)이면, \(C\)는 cone ( 혹은 non-negative homogenous )이다

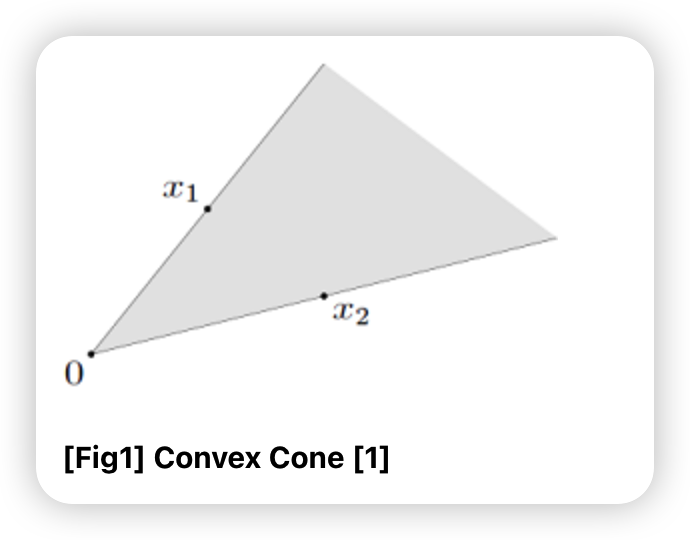
Convex Cone

• \(\theta_{1} x_{1}+\theta_{2} x_{2} \in C\) with \(x_{1}, x_{2} \in C, \theta_{1}, \theta_{2} \geq 0\)
• 집합 \(C\)가 cone & convex 둘다 만족할 경우!

Conic Combination

• \(\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{k} x_{k}\) with \(\theta_{i} \geq 0, i=1, \ldots, k\)
• 특징 : 계수의 합을 제한은 없음 + only 양수 제한
• cone의 정의
  • 집합 \(C\)에 속하는 임의의 여러 점들의 conic combination이 다시 집합 \(C\)에 속하면, conic set이다

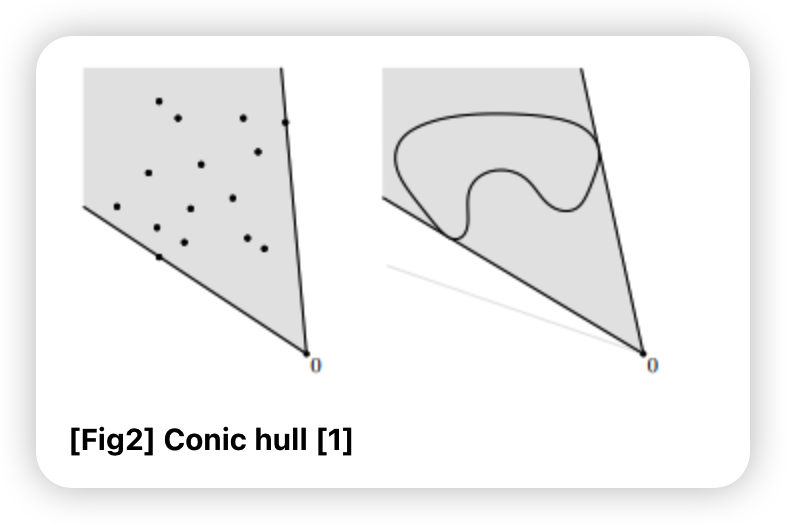
Conic Hull

• \(\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{i} \in C, \theta_{i} \geq 0, i=1, \ldots, k\right\}\).
• conic combination들의 집합 ( 집함 \(C\)를 포함하는 가장 작은 affine set )

2-2. Examples

• Trivial ones: empty set, point, line, line segment, ray
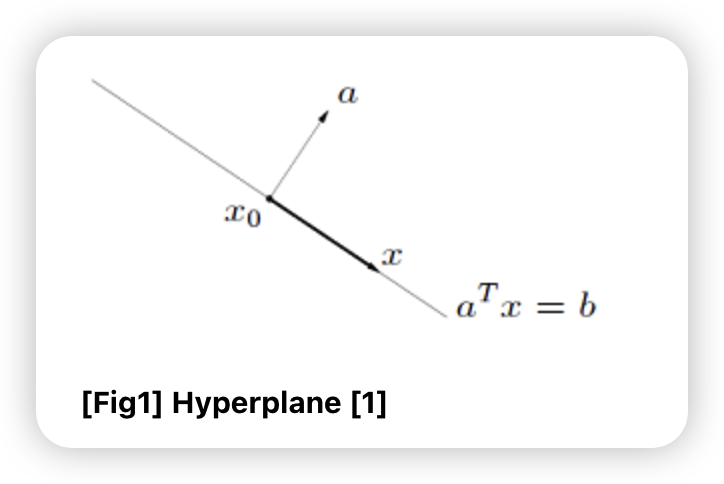
• Hyperplane: \(\left\{x: a^{T} x=b\right\}\), for given \(a, b, a \neq 0\)
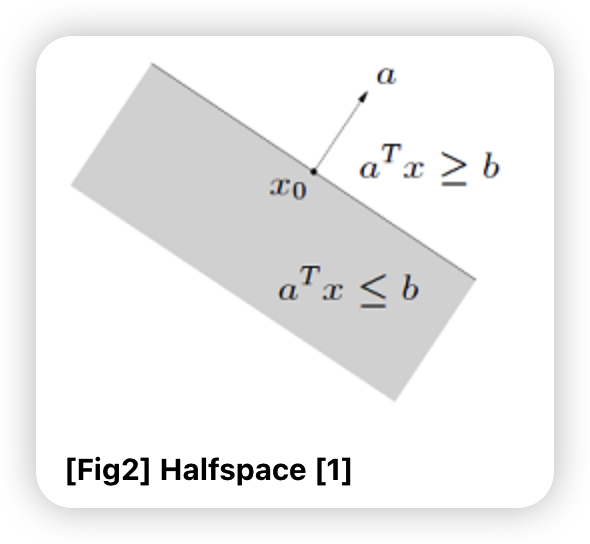
• Halfspace: \(\left\{x: a^{T} x \leq b\right\}\) for \(a \neq 0\)
• Affine space: \(\{x: A x=b\}\), for given \(A, b\)
• Euclidean ball \& ellipsoid
• Norm ball: \(\{x: \mid \mid x \mid \mid \leq r\}\), for given norm \(\mid \mid \cdot \mid \mid\), radius \(r\)
• Convex cone : norm cone, normal cone, positive semidefinite cone

[ Convex Set의 예시들 ]

a) Hyperplanes

\(\left\{x: a^{T} x=b\right\}\) with \(a \in R^{n}, a \neq 0, b \in R\)

b) Halfspaces

\(\left\{x: a^{T} x \leq b\right\}\) or \(\left\{x: a^{T} x \geq b\right\}\) with \(a \in R^{n}, a \neq 0, b \in R\)

• open halfspace : \(\left\{x: a^{T} x < b\right\}\) or \(\left\{x: a^{T} x > b\right\}\)

c) Euclidean balls

\(B\left(x_{c}, r\right)=\left\{x \mid \mid \mid x-x_{c} \mid \mid _{2} \leq r\right\}=\left\{x \mid\left(x-x_{c}\right)^{T}\left(x-x_{c}\right) \leq r^{2}\right\} \text { with } r \geq 0\) with \(r \geq 0\)

( 혹은 \(B\left(x_{c}, r\right)=\left\{x_{c}+r u \mid \mid \mid u \mid \mid _{2} \leq 1\right\}\) )

• \(\mid \mid . \mid \mid _{2}\) : euclidean norm … \(\mid \mid u \mid \mid _{2}=\left(u^{T} u\right)^{\frac{1}{2}}\)

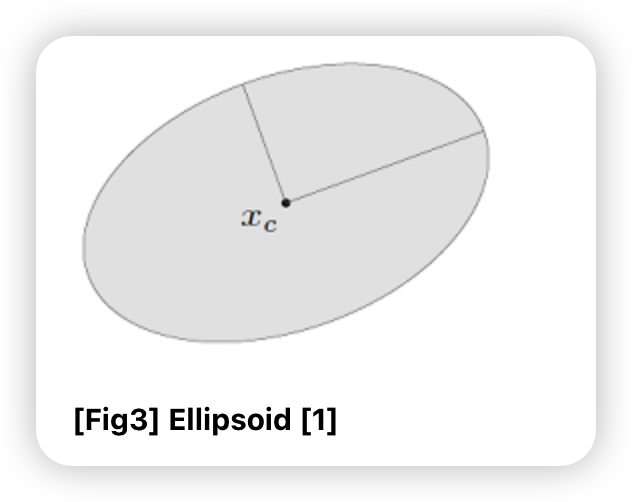
d) Ellipsoids

\[\mathcal{E}=\left\{x \mid\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leq 1\right\}\]

• 타원 모양
• \(P=P^{T} \succ 0\) 로 \(P\) 는 symmetric이고 positive definite
  • 중심에서 모든 방향으로 얼마나 나아가는지를 의미
• 축 : \(\sqrt{\lambda_{i}}\)
  • \(\lambda_{i}\) : \(P\) 의 eigenvalue
• ball : \(P=r^{2} I\) 인 ellipsoid

다른 표현

\(\mathcal{E}=\left\{x_{c}+A u \mid \mid \mid u \mid \mid _{2} \leq 1\right\}\).

• \(A\) 는 square & nonsingular

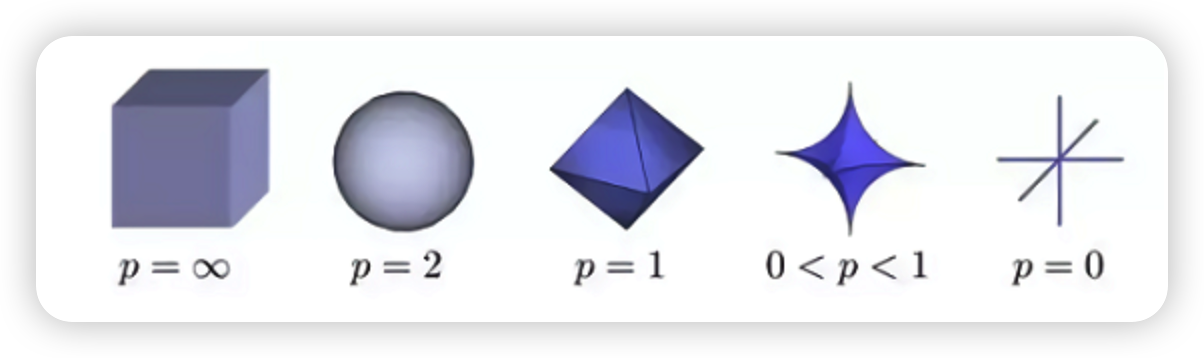
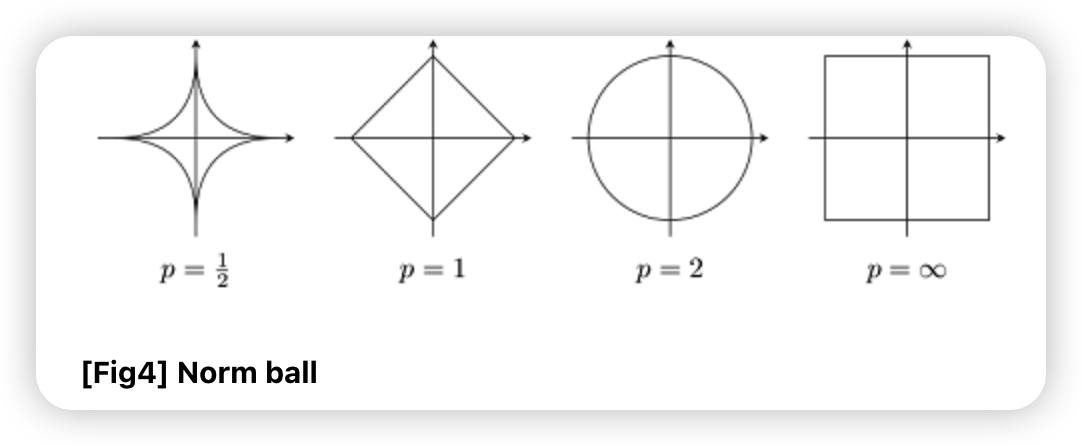
e) Norm balls

( euclidean norm의 general version )

\(\left\{x \mid \mid \mid x-x_{c} \mid \mid \leq r\right\}\).

• \(p\)-norm : \(\mid \mid x \mid \mid _{p}=\left(\sum_{i=0}^{n} \mid x_{i} \mid ^{p}\right)^{1 / p}\) for \(p \geq 1\)

f) Polyhedra

\(\mathcal{P}=\left\{x \mid a_{i}^{T} x \leq b_{i}, i=1, \ldots, m, c_{j}^{T} x=d_{j}, j=1, \ldots, p\right\}\).

• solution set of “finitely many linear inequalities & equalities”
• intersection of finite number of halfspaces & hyperplanes

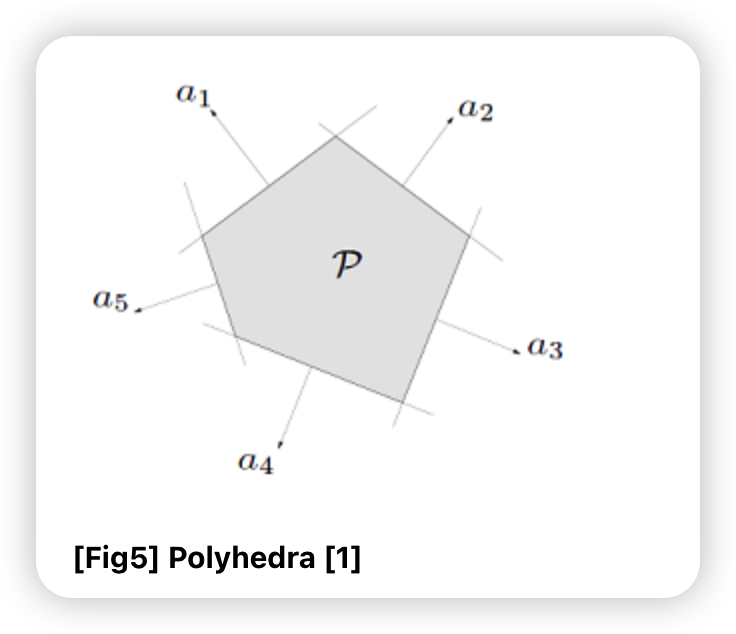
행렬 notation : \(\mathcal{P}=\left\{x \mid A^{T} x \preceq b, C^{T} x=d\right\}\)

Simplex

• \(n\) 차원 공간에서 만들 수 있는 가장 간단한 다각형
• \(n+1\)개의 점으로 만들어짐
  • ex) 2차원 : 삼각형
  • ex) 3차원 : 사면체
• Ex) probability simplex
  • \(C=\operatorname{conv}\left\{e_{1}, \ldots, e_{n}\right\}=\left\{\theta \mid \theta \succeq 0,1^{T} \theta=1\right\}\).

[ Convex Cone의 예시들 ]

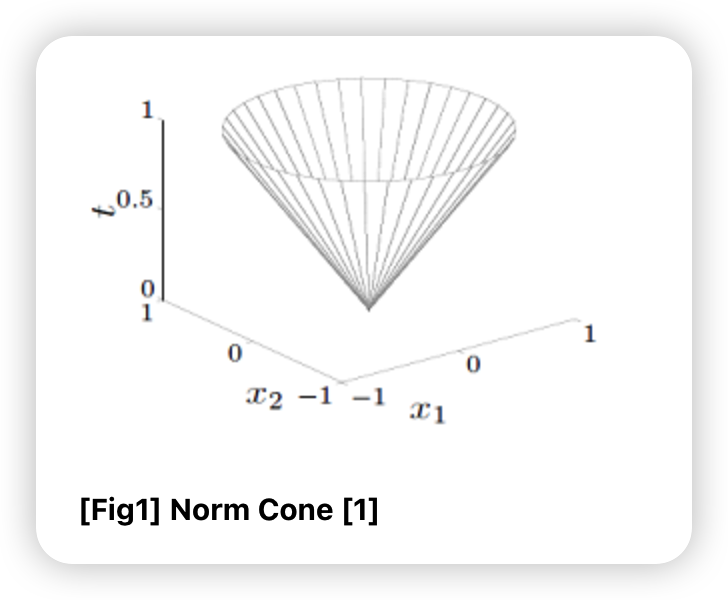
a) Norm Cone

\(C=\{(x, t): \mid \mid x \mid \mid \leq t\} \subseteq R^{n+1} \text {, for a norm } \mid \mid \cdot \mid \mid\).

• 반경 \(t\) 이내의 점들로 이뤄진 cone
• second-order cone / ice-cream cone

2-3. Operations that preserve convexity

1. Intersection
   • \(S=\bigcap\{\mathcal{H} \mid \mathcal{H}\) halfspace, \(S \subseteq \mathcal{H}\}\)
2. Affine functions
   • \(f: R^{n} \rightarrow R^{m}\) 인 \(f(x)=A x+b\)

3. Perspective function

   • If \(f: \mathbf{R}^{n} \rightarrow \mathbf{R}\), then the perspective of \(f\) is the function \(g: \mathbf{R}^{n+1} \rightarrow \mathbf{R}\) defined by

     \[g(x, t)=t f(x / t),\]

     with domain \(\operatorname{dom} g=\{(x, t) \mid x / t \in \operatorname{dom} f, t>0\} .\)

4. Linear-fractional functions
   • \(f(x)=(A x+b) /\left(c^{T} x+d\right), \text { dom } f(x)=\left\{x \mid c^{T} x+d>0\right\}\left(A \in R^{m \times n}, b \in R^{m}, c \in R^{n}, d \in R\right)\).
   • example)
     • \(f(x) = \frac{1}{x_1+x_2+1}x\),
     • dom \(f(x) = \{(x_1,x_2) \mid x_1 + x_2 + 1 >0 \}\)

2-4. Generalized inequalities

• 1차원 공간 : 3>1 (비교 쉬워)

• n차원 공간 : \(x_1\) & \(x_2\)의 비교는?

\(\rightarrow\) generalized inequality에 대해 알아보자

Proper cone

convex cone \(K\)가 다음을 만족하면, proper cone

• (1) closed ( 경계 포함 )
• (2) solid ( 내부가 비어있지 X )
• (3) pointed ( 직선 포함 X )
  • 즉, \(x \in K, -x \in K\)이면, \(x=0\)

Generalized Inequality

proper cone을 이용해서 정의하기

• standard ordering

2-5. Separating & Supporting hyperplanes

• 생략

2-6. Dual cones & Generalized inequalities

• 생략