07. Subgradient
7-1. Subgradient
convex function \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) 에 대하여, 다음을 만족하는 \(g \in \mathbb{R}^{n}\) 는 \(f\) 의 subgradient
- \(f(y) \geq f(x)+g^{T}(y-x), \text { for all } y\).
직관적인 의미 :
- NON-differentiable한 convex function의 gradient에 대한 일반화!
- 2가지 경우
- differentiable : \(\nabla f(x)\) 가 유일한 \(g\)
- Non-differentiable : 구할수도, 못 구할수도
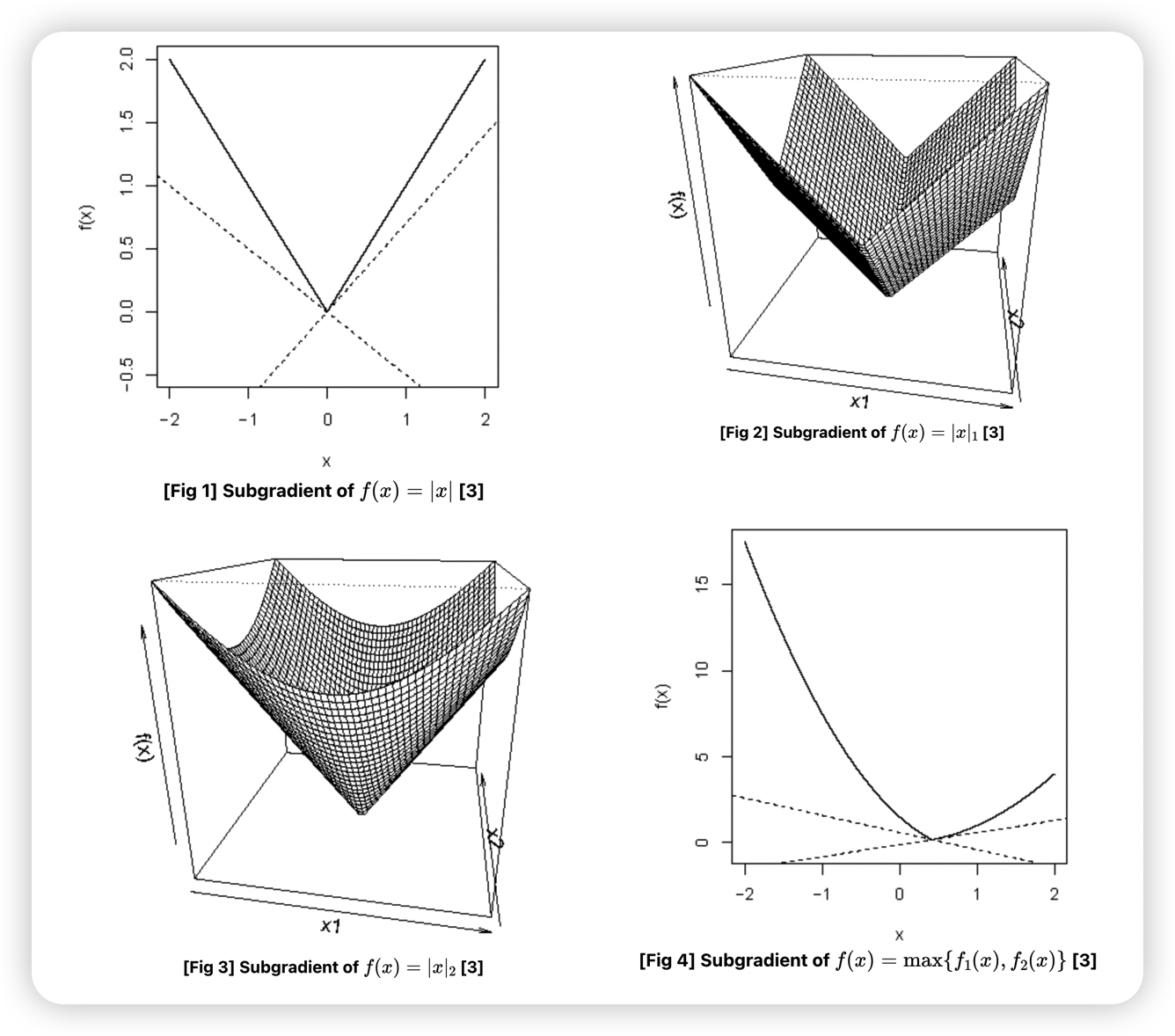
Example 1 ) \(f: \mathbb{R} \rightarrow \mathbb{R}, f(x)= \mid x \mid\)
- \(x \neq 0\) : \(g = \text{sign}(x)\)
- \(x=0\) : \(g \in [-1,1]\)
Example 2 ) \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}, f(x)= \mid \mid x \mid \mid _{1}\)
- \(x \neq 0\) : \(g_i = \text{sign}(x_i)\)
- \(x_i=0\) : \(g_i \in [-1,1]\)
( for \(i\) in \(1, \cdots n\) )
Example 3 ) \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}, f(x)= \mid \mid x \mid \mid _{2}\)
- \(x \neq 0\) : \(g=\nabla \sqrt{x^{T} x}=\frac{1}{2}\left(x^{T} x\right)^{-\frac{1}{2}}(2 x)=\frac{x}{ \mid \mid x \mid \mid _{2}}\)
- \(x_i=0\) : \(g \in\left\{z: \mid \mid z \mid \mid _{2} \leq 1\right\}\)
( for \(i\) in \(1, \cdots n\) )
Example 4) \(f(x)=\max \left\{f_{1}(x), f_{2}(x)\right\}\) … where \(f_{1}, f_{2}: \mathbb{R}^{n} \rightarrow \mathbb{R}\)
- \(f_{1}(x)>f_{2}(x)\) : \(g=\nabla f_{1}(x)\).
-
\(f_{1}(x)<f_{2}(x)\) : \(g=\nabla f_{2}(x)\).
- \(f_{1}(x)=f_{2}(x)\) : \(g \in\left\{\theta_{1} \nabla f_{1}(x)+\theta_{2} \nabla f_{2}(x): \theta_{1}+\theta_{2}=1, \theta_{1} \geq 0, \theta_{2} \geq 0\right\}\).