Continual Learning (1) - Regularization-based CL

Contents

1. Background
2. EWC (Elastic Weight Consolidation)
3. SI (Synaptic Intelligence)
4. MAS (Memory Aware Synapses)
5. Summary

Background

Continual Learning (CL)의 필요성:

• Catastrophic Forgetting

CL의 3가지 Scenario

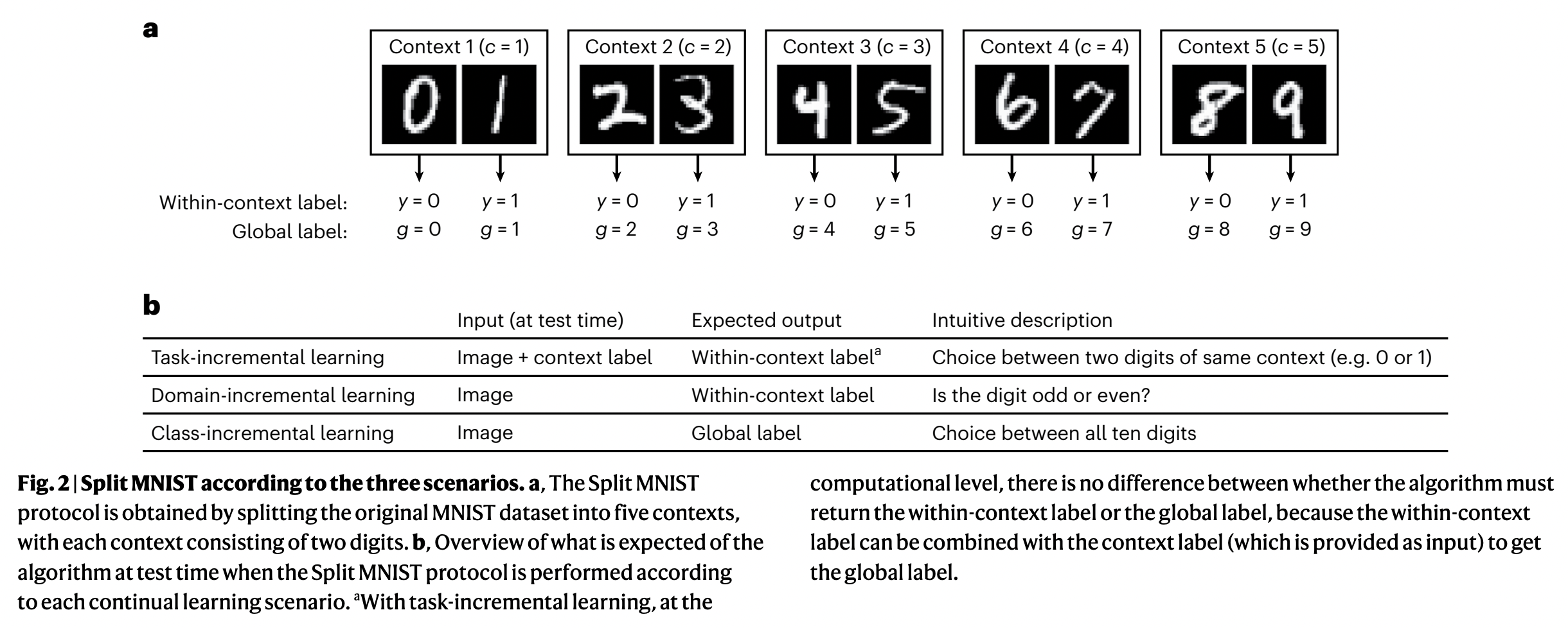
• Task-Incremental Learning (Task-IL)
• Domain-Incremental Learning (Domain-IL)
• Class-Incremental Learning (Class-IL)

Frameworks

전략 종류	대표 기법	설명
(1) Regularization-based	EWC, SI, MAS	param 이동 억제
(2) Replay-based	ER, A-GEM, DER++	예전 데이터(또는 생성 데이터) 재사용
(3) Parameter isolation	PNN, HAT, PackNet	task별 서브네트워크 유지
(4) Dynamic architecture	DEN, ExpandNet	필요시 네트워크 구조 확장

1. EWC (Elastic Weight Consolidation)

Kirkpatrick et al., “Overcoming catastrophic forgetting in neural networks”, PNAS 2017

https://arxiv.org/abs/1612.00796

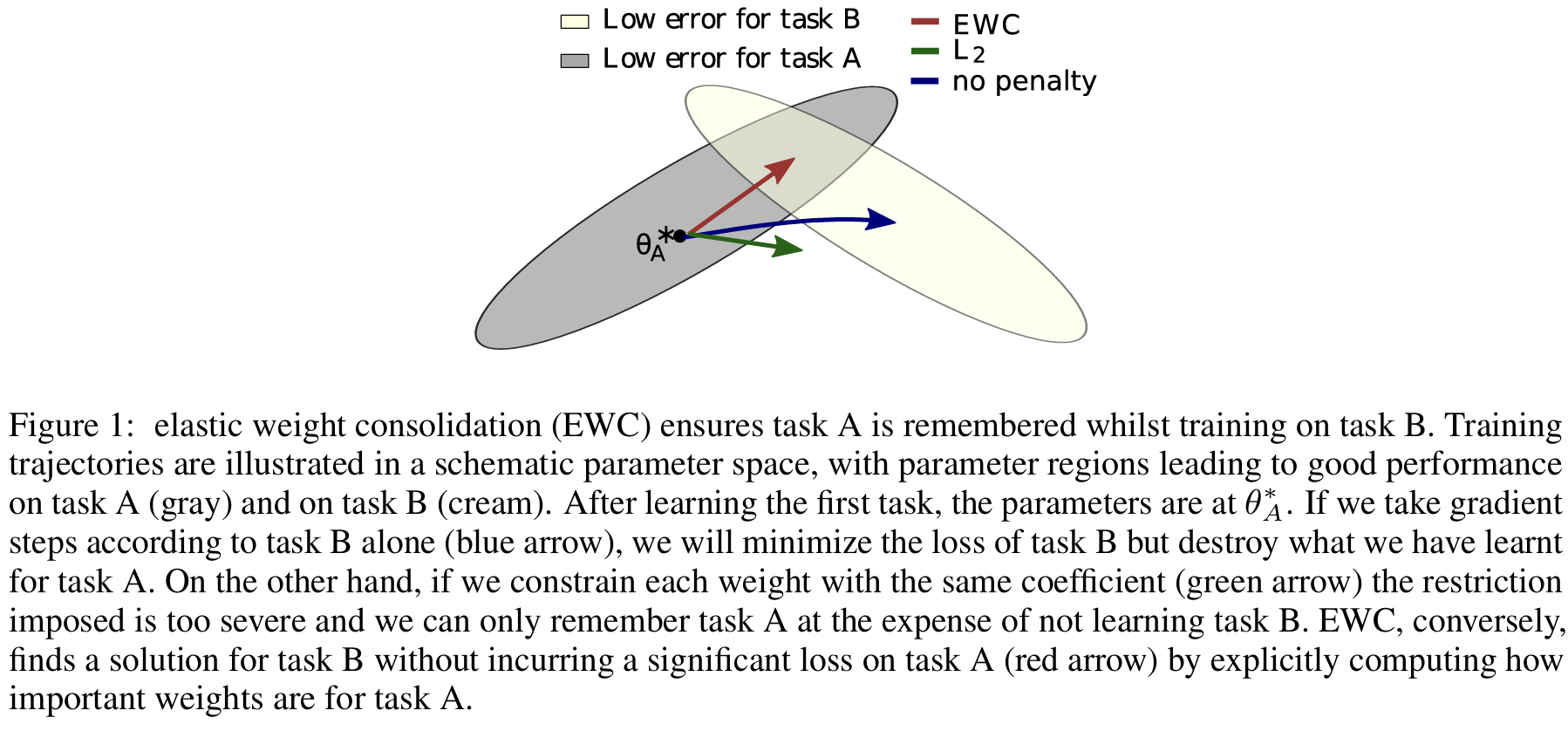
(1) Key Idea

“이전 task에서 중요했던 파라미터는 많이 바뀌지 않도록 하자.”!

• 파라미터의 중요도 = by Fisher Information Matrix (FIM)
• 바뀌지 않게 하자 = by Regularization term

(2) Regularization Loss

(w/o Reg) \(\mathcal{L}_{\text{task}}(\theta)\)

(w/ Reg) \(\mathcal{L}_{\text{total}}(\theta) = \mathcal{L}_{\text{task}}(\theta) + \lambda \sum_i F_i (\theta_i - \theta_i^*)^2\)

• \(\theta_i\): 현재 파라미터
• \(\theta_i^*\): 이전 task에서 학습한 파라미터
• \(F_i\): param \(\theta_i\)의 Fisher information (중요도)
• \(\lambda\): Reg strength

(3) Fisher Information Matrix (FIM)

\(F_i = \mathbb{E}_{x \sim D} \left[ \left( \frac{\partial \log p(y \mid x, \theta)}{\partial \theta_i} \right)^2 \right]\).

• 핵심: param이 log prob를 얼마나 민감하게 변화시키는가
• \(F_i\)가 크다 = 해당 param은 모델 예측에 중요한 역할을 함

(4) Procedure

1. Task A 학습
2. 학습 완료 후:
   • 각 파라미터에 대해 \(F_i\), \(\theta_i^*\) 저장
3. Task B 학습:
   • 손실 함수에 reg loss 추가하여 EWC 적용

(5) Code

def ewc_loss(model, fisher, theta_old, lambda_ewc):
    loss_reg = 0
    for name, param in model.named_parameters():
        if name in fisher:
            loss_reg += (fisher[name] * (param - theta_old[name])**2).sum()
    return lambda_ewc * loss_reg

• fisher: 각 파라미터의 FIM 추정값 (사전 저장)
• theta_old: 이전 task의 param 복사본

(6) Pros & Cons

Pros

• 간단하고 직관적
• 대부분의 모델에 쉽게 적용 가능

Cons

• FIM 계산이 비용이 큼 (보통 diagonalization)
• 모든 파라미터를 동일한 방식으로 제약 (layerwise 조정 불가)

2. SI (Synaptic Intelligence)

Zenke et al., “Continual Learning Through Synaptic Intelligence”, ICML 2017

https://arxiv.org/abs/1703.04200

(1) Key Idea

학습 중에, 각 파라미터가 “손실 감소”에 얼마나 기여했는지 추적

\(\rightarrow\) 그 정보로 param의 중요도를 추정!

if 높은 중요도 \(\rightarrow\) 이후 task에서 변화하지 않도록 규제

(2) EWC vs. SI

항목	EWC	SI
Param 중요도 계산 시점	학습 끝나고 (Fisher 정보로 계산)	학습 중 매 step
계산 비용	FIM 필요	Param 변화량만 추적 필요
적용 가능 환경	Task의 끝을 알아야 함	온라인 학습에 적합

(3) Regularization Loss

\(\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{task}} + \lambda \sum_i \Omega_i (\theta_i - \theta_i^*)^2\).

• \(\Omega_i\): Param의 중요도

  \(\rightarrow\) 학습 과정에서 계속해서 직접 추적!

(4) Parameter Importance

\(\omega_i \leftarrow \omega_i + \Delta \theta_i \cdot -g_i\).

• \(\Delta \theta_i\): 이번 step에서 param의 변화량
• \(g_i\): 이번 step에서의 그라디언트

\(\rightarrow\) 둘의 내적 = “해당 변화가 손실을 얼마나 줄였는가“

\(\Omega_i = \frac{\omega_i}{(\Delta \theta_i)^2 + \epsilon}\).

• 의미 = 총 기여량 / 총 변화량

• 이 값이 높을 수록, Param 변화 적음!

(5) Procedure

1. 학습 중 매 step마다 \(\Delta \theta, g, \omega\) 업데이트
2. 한 task 끝나면 \(\Omega\) 계산
3. 다음 task부터는:
   • \(\Omega\) 기반 reg loss 추가
   • 이전 param\(\theta_i^{*}\)도 저장

(6) Code

# 학습 중
for name, param in model.named_parameters():
    delta = param.data - prev_param[name]
    grad = param.grad
    omega[name] += (delta * -grad).detach().clone()
    prev_param[name] = param.data.clone()

# task 종료 후
for name in omega:
    delta_sq = (param[name] - prev_param[name]) ** 2 + epsilon
    importance[name] = omega[name] / delta_sq

(7) Pros & Cons

Pros

• Online으로 학습
• task 경계가 없어도 사용 가능

Cons

• 모든 param변화량과 그라디언트를 매 step마다 저장/추적해야!
• 학습 속도에 부하 있음
• 여전히 quadratic penalty

3. MAS (Memory Aware Synapses)

Aljundi et al., “Memory Aware Synapses: Learning What (Not) to Forget”, ECCV 2018

https://arxiv.org/abs/1711.09601

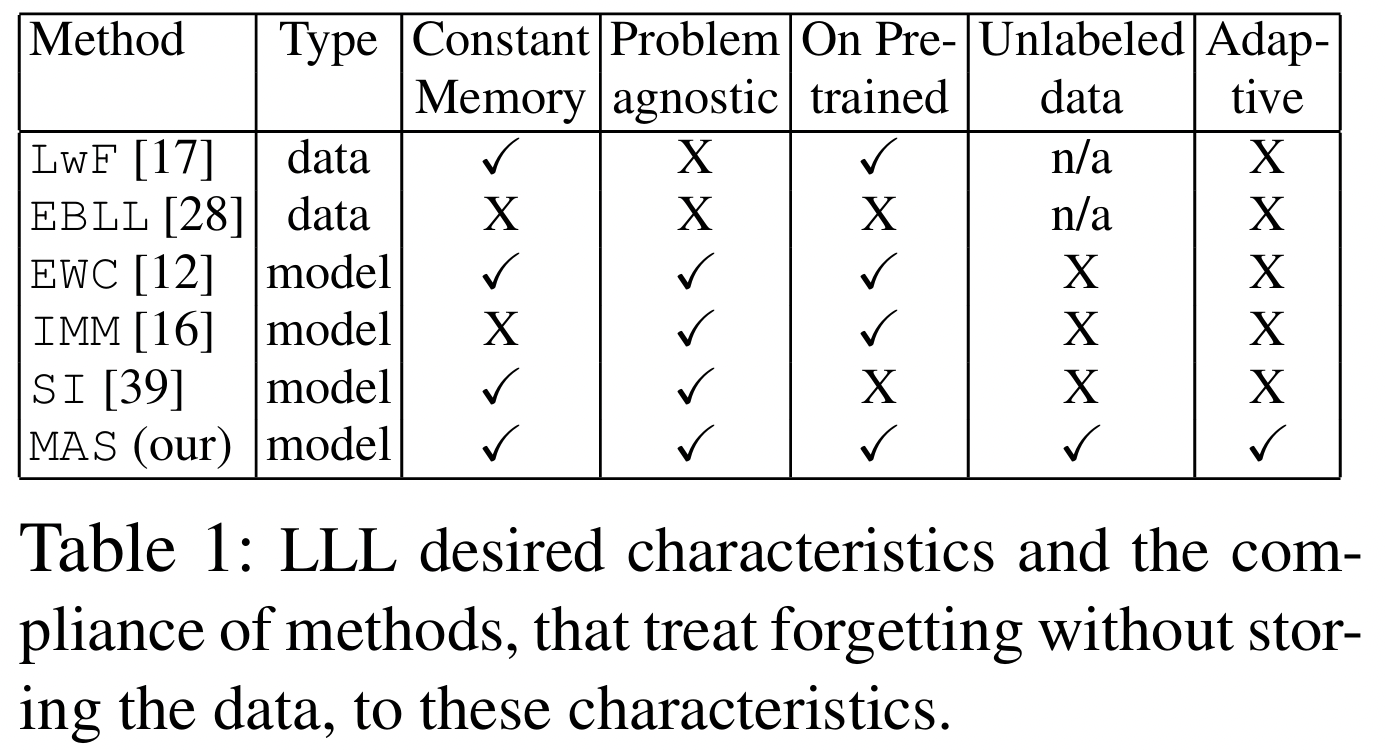
(1) Key Idea

모델이 output에 민감하게 영향을 미치는 param일수록, 잊지 않도록(=변경을 억제) !

• 이전 task에서 출력에 영향을 많이 준 파라미터는
• 다음 task에서 변화하지 않도록 regularization을 추가

(2) EWC/SI vs. MAS

항목	MAS	EWC / SI
기반	Output 민감도	Log prob / Loss
Label 필요성	Unsupervised	Supervised
계산 시점	task 종료 후	EWC: 종료 후 / SI: 학습 중

(3) Regularization Loss

\(\Omega_i = \mathbb{E}_{x \sim D} \left[ \mid \mid \frac{\partial f(x)}{\partial \theta_i} \mid \mid \right]\).

• \(f(x)\): 모델의 출력

• \(\frac{\partial f(x)}{\partial \theta_i}\): 해당 param이 output에 얼마나 영향을 주는지

  \(\rightarrow\) 클 수록 중요한 param

\[\mathcal{L}_{\text{MAS}} = \lambda \sum_i \Omega_i \cdot (\theta_i - \theta_i^*)^2\]

• \(\theta^*_i\): 이전 task 학습이 끝난 후의 param값
• \(\Omega_i\): 중요도

(4) 출력 민감도

• 기존 방법(EWC, SI)은 Label & Loss func가 필요하

• MAS는 only output만 필요

  \(\rightarrow \therefore\) unsupervised 환경에서도 작동 가능!

(5) Procedure

1. task A 학습 종료
2. 학습된 모델을 freeze한 뒤:
   • \(x\)를 입력하고
   • \(f(x)\)의 각 파라미터에 대한 gradient 크기 측정
   • 평균 내서 \(\Omega_i\) 계산

(6) Code

for data in dataloader:
    data = data.requires_grad_(True)
    output = model(data)
    loss = output.norm(2)  # 출력 전체에 대해 norm
    loss.backward()

    for name, param in model.named_parameters():
        if param.grad is not None:
            importance[name] += param.grad.abs()

(7) Pros & Cons

Pros

• Unsupervised

• Output에만 의존 (계산 단순 & 안정적)

Cons

• loss gradient 기반 방식들보다는 예측 중심 해석이 어려움

• 모든 파라미터가 출력에 영향을 주는 건 아님 (특히 초기 layer)

4. Summary

알고리즘	핵심 아이디어	중요도 측정 방식	장점	한계
EWC	FIM 기반 정규화	Fisher Information	간단, 널리 사용	계산량 큼, task 많으면 경직
SI	학습 기여 기반	param경로 추적	온라인, 효율적	구현 복잡
MAS	출력 민감도 기반	activation gradient	비지도 가능	해석 제한적