Continual Learning (2) - Replay-based CL

Contents

1. Background
2. ER (Experience Replay)
3. A-GEM (Average Gradient Episodic Memory)
4. iCaRL (Incremental Classifier and Representation Learning)

Background

Continual Learning (CL)의 필요성:

• Catastrophic Forgetting

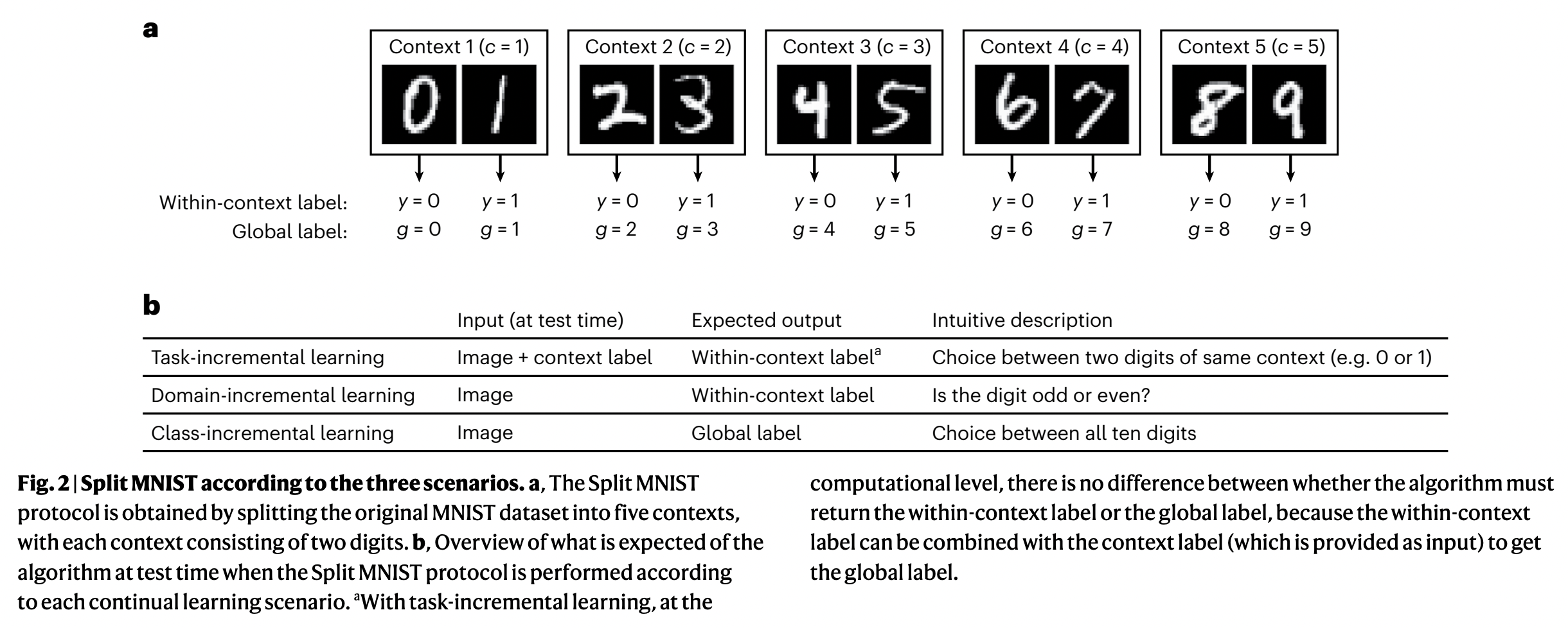
CL의 3가지 Scenario

• Task-Incremental Learning (Task-IL)
• Domain-Incremental Learning (Domain-IL)
• Class-Incremental Learning (Class-IL)

Frameworks

전략 종류	대표 기법	설명
(1) Regularization-based	EWC, SI, MAS	param 이동 억제
(2) Replay-based	ER, A-GEM, DER++	예전 데이터 (또는 생성 데이터) 재사용
(3) Parameter isolation	PNN, HAT, PackNet	task별 서브네트워크 유지
(4) Dynamic architecture	DEN, ExpandNet	필요시 네트워크 구조 확장

1. ER (Experience Replay)

Lopez-Paz et al., “Gradient Episodic Memory (GEM)”, NeurIPS 2017

https://arxiv.org/abs/1706.08840

(1) Key Idea

가장 단순 & 직관적인 replay 기반 방법

• 이전 task의 “데이터를 조금씩 저장”해두고,
• 새로운 task를 학습할 때 “다시 같이 학습”

단, 전체 데이터를 저장하면 비효율적이므로

→ “일부” sample만 메모리 버퍼 (memory buffer)에 저장!

(2) Components

요소	설명
Buffer	과거 sample들을 저장하는 공간 (크기 제한 있음)
Main loss	현재 task 데이터로 계산한 loss
Replay loss	buffer에 저장된 과거 데이터로 계산한 loss
Total loss	Main loss + Replay loss

(3) Procedure

• Step 1) Task A 학습

• Step 2) Task A에서 본 데이터 일부를 메모리에 저장

• Step 3) Task B 학습 시, 아래 둘 다 활용!
  • (a) Task B 데이터
  • (b) Memory buffer 데이터
• Step 4) Buffer는 계속 업데이트
  • e.g., FIFO, reservoir sampling 등

(4) Loss Function

\(\mathcal{L}_{\text{total}} = \mathcal{L}(\mathcal{D}_t) + \lambda \cdot \mathcal{L}(\mathcal{M})\).

• \(\mathcal{D}_t\): 현재 task의 데이터
• \(\mathcal{M}\): Memory buffer
• \(\mathcal{L}\): Loss function (e.g., cross-entropy)
  • 보통 \(\lambda = 1\): 단순히 두 배치 합쳐서 학습

(5) Code

# 메모리 버퍼
memory = []

# 현재 배치와 memory 혼합
inputs = torch.cat([current_inputs, memory_inputs])
labels = torch.cat([current_labels, memory_labels])

# forward & backward
logits = model(inputs)
loss = criterion(logits, labels)
loss.backward()
optimizer.step()

(6) Memory Buffer

• FIFO: 오래된 것부터 제거
• Reservoir Sampling: 무작위로 대체 (uniform prob.)
• Herding / Diversity 기반 선택: representativeness 고려

(7) Pros & Cons

Pros

• 개념이 매우 직관적이고 구현 쉬움
• 잘만 쓰면 성능이 꽤 높음

Cons

• “메모리를 얼마나, 어떻게 채우느냐”에 따라 성능이 매우 달라짐
• Task 간 간섭 (interference) 가능성 존재 (같은 class라도 분포가 다르면 문제)
• Class-Incremental 환경에서는 Label ambiguity 이슈 발생

(8) Class-IL & Label Ambiguity

Class-Incremental Learning: ask가 바뀔수록 새로운 class들이 추가됨

\(\rightarrow\) 매 task마다 class가 증가하고, 모델은 이전 class까지 전부 구분해야!

한계점: Replay 방식에서는 라벨 혼동(label ambiguity)이 발생할 수 있음

이유?

• Replay는 과거 task 데이터의 입력과 라벨을 그대로 저장해서 재학습에 사용함.
• 하지만 현재 모델은 과거 task의 class 정보 자체를 잊고 있음.

2. A-GEM (Average Gradient Episodic Memory)

Chaudhry et al., “Efficient Lifelong Learning with A-GEM”, ICLR 2019

https://arxiv.org/abs/1812.00420

(1) Key Idea

단순히 과거 데이터를 함께 학습하는 것에서 넘어서서…

과거 task의 성능이 떨어지지 않도록 “gradient 방향을 조절”하자!

How? 과거 task의 성능을 해치지 않는 방향으로만 param를 업데이트!

(2) Motivation

Naive한 ER처럼 과거 데이터를 그냥 섞어서 학습하면…

\(\rightarrow\) 현재 task에 유리한 방향으로 gradient가 쏠릴 수 있음!

→ Catastrophic forgetting!!

(3) Components

구성 요소	설명
Memory buffer \(\mathcal{M}\)	과거 task에서 저장된 sample
Current gradient \(g\)	현재 task 데이터에 대한 gradient
Reference gradient \(g_{\text{ref}}\)	메모리 sample에 대한 gradient
Projection step	\(g \cdot g_{\text{ref}} < 0\) 이면 → \(g\)를 \(g_{\text{ref}}\) 방향으로 projection

(4) Gradient

Gradient

• 현재 gradient: \(g = \nabla_\theta \mathcal{L}_{\text{current}}\)

• 메모리 gradient: \(g_{\text{ref}} = \nabla_\theta \mathcal{L}_{\text{memory}}\)

검열 조건:

• \(g \cdot g_{\text{ref}} < 0 \Rightarrow \text{interfering}\) == 과거 기억 손상 == Catastrophic Foregetting

Projection

• \(g’ = g - \frac{g^\top g_{\text{ref}}}{ \mid g_{\text{ref}} \mid ^2} g_{\text{ref}}\).

  → 즉, g를 g_{\text{ref}}에 수직이 되도록 projection

(5) Code

# 1. 현재 task 데이터에 대한 gradient 계산
loss_current = criterion(model(x_current), y_current)
loss_current.backward()
g = get_gradient_vector(model)
model.zero_grad()

# 2. 메모리(이전 task) 데이터에 대한 gradient 계산
loss_memory = criterion(model(x_memory), y_memory)
loss_memory.backward()
g_memory = get_gradient_vector(model)
g_ref.zero_grad()

# dot product
if g.dot(g_ref) < 0:
    # projection
    g = g - (g.dot(g_ref) / g_ref.norm()**2) * g_ref

# assign back and step
set_grad_vector(model, g)
optimizer.step()

(6) Pros & Cons

Pros

• Forgetting이 크게 감소
• ER보다 더 적은 replay 데이터로도 높은 성능
• 메모리 효율적

Cons

• gradient 계산을 두 번 해야 함 (현재 + memory)
• 하나의 reference gradient에만 기반 → 정확한 past loss 보장 X
• 완전한 interference 방지는 아님

(7) ER vs. A-GEM

항목	ER	A-GEM
Replay 방식	sample 직접 학습	gradient 비교 후 projection
성능 보존	안 될 수 있음	일정 수준 이상 보장
구현 난이도	매우 쉬움	중간 (gradient 조작 필요)

3. iCaRL (Incremental Classifier and Representation Learning)

Rebuffi et al., “iCaRL: Incremental Classifier and Representation Learning”, CVPR 2017

https://arxiv.org/abs/1611.07725

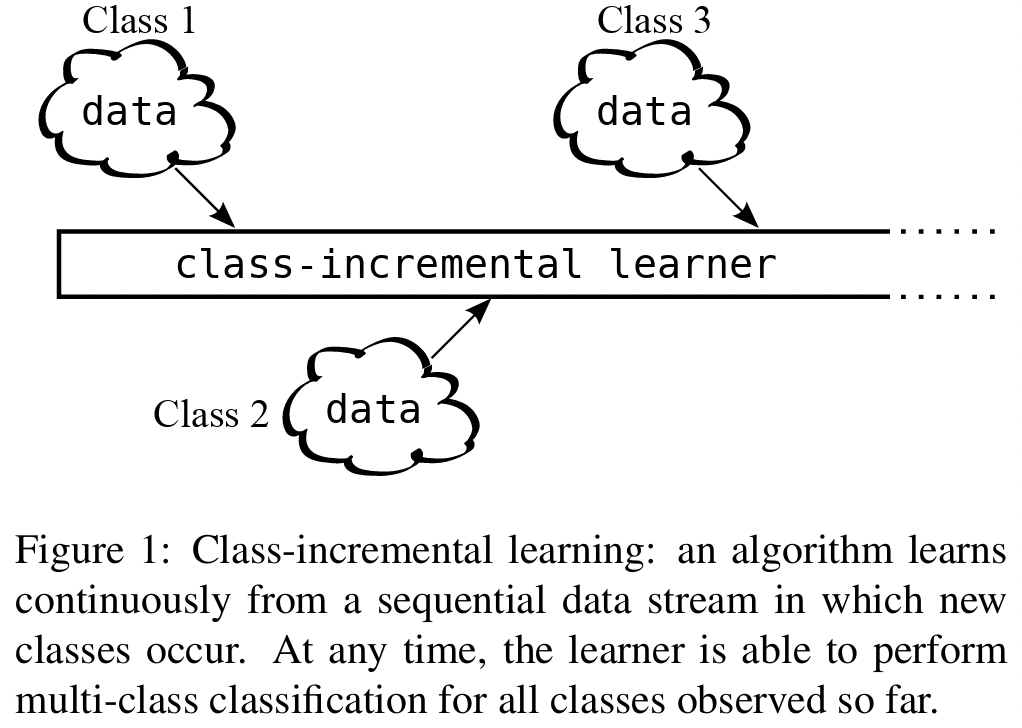
(1) Class-Incremental Learning (Class-IL)

• 매 task마다 새로운 class들이 추가
• 모든 class를 구분해야!
• 제약 사항
  • Task ID를 알 수 없음
  • Label ambiguity 문제가 발생함

(2) Key Idea

단순히 Replay만 하는 것이 아니라…

Representation을 학습하면서도 과거 class의 분류 능력을 유지하기 위해

다음 3가지 기법을 결합함:

구성 요소	설명
1. Exemplar memory	각 class에서 일부 sample만 저장
2. Nearest-class-mean classifier	sample 평균을 기준으로 분류
3. Feature distillation	과거 모델의 output을 따라하게 학습 (망각 방지)

(3-1) Exemplar Memory

각 class별로 대표적인 sample 몇 개(exemplars)만 저장해두고,
이전 class의 특성을 유지하거나 분류할 때 사용하자!

• 매 class마다 대표 sample 몇 개만 저장
• 메모리 용량 K이 고정되어 있으면:
  • class가 늘어날수록 class당 저장 수는 줄어듬
• “herding” 기법을 사용해 가장 대표적인 sample을 선택

Herding Algorithm

= 각 class에 대해 feature space에서 평균과 가장 가까운 sample들을 선택

• class \(C\)의 평균 feature \(\mu_C\)를 계산
• 그 평균에 가장 가까운 sample부터 차례대로 뽑음

Procedure

1. 모든 sample \(x_i \in C\)에 대해 feature vector \(f(x_i)\)를 추출
2. class 평균 벡터 계산:
   • \(\mu_C = \frac{1}{N} \sum_{i=1}^{N} f(x_i)\).
3. 반복적으로 가장 가까운 sample 선택:
   • \(p_k = \arg\min_{x_i \in C} \mid \mu_C - \frac{1}{k} \sum_{j=1}^{k-1} f(p_j) + f(x_i) \mid\).

(3-2) Nearest-class-mean (NCM) classifier

저장된 exemplar들의 feature를 사용해
class마다 대표 feature 평균 벡터(class mean)를 만들고,
새로운 입력의 feature와 가장 가까운 mean을 찾아 분류!

• class마다 저장된 exemplar들의 feature 평균을 계산

• 테스트 시 입력 sample의 feature 벡터와 비교하여 가장 가까운 class로 분류

  • \(\hat{y} = \arg\min_k \mid f(x) - \mu_k \mid _2\).

    • \(f(x)\): backbone이 output한 feature representation

    • \(\mu_k\): class \(k\)의 exemplar 평균 feature

Q) Why not Softmax?

A) (Class-incremental 상황에서) Softmax classifier 사용 시의 문제점

• Softmax는 모든 class에 대한 output을 “재학습”해야!
• 이전 class의 데이터가 없는 상황에서는 output이 무너지거나 drift하게 됩니다.

\(\rightarrow\) \(\therefore\) (output 대신) “feature space 상의 거리” 기반 분류를 사용

장점

• Task-ID 없이도 모든 class를 구분할 수 있음 → Class-IL에 적합
• 이전 class의 분류기를 따로 재학습할 필요 없음
• feature drift에만 주의하면 강건한 분류기

단점

• feature representation이 변하면 class mean도 같이 무너짐

  → 그래서 iCaRL은 다음 구성 요소인 feature distillation을 추가로 사용합니다

• class 간 분포가 overlap할 경우 성능 저하

(3-3) Feature Distillation

모델이 "이전 클래스"에 대해 학습했던 feature 표현(feature representation)을 기억하고 유지할 수 있도록 돕는 기법

Motivation

• iCaRL은 분류할 때 feature space에서 class mean과 거리를 비교

• But, backbone network가 다음 태스크에서 바뀌면:

  • 이전에 저장해둔 exemplar의 feature와
  • 현재 모델이 뽑아낸 feature가 매치되지 않음

  → NCM 분류기 실패 → catastrophic forgetting!

Details

• 이전 모델이 output한 feature representation \(f_{\text{old}}(x)\)를 저장
• 다음 task 학습 시 지금 모델의 feature \(f(x)\)가 과거 모델과 비슷하게 유지되도록
  • \(\mathcal{L}{\text{distill}} = \sum_x \mid f(x) - f{\text{old}}(x) \mid ^2\).
• Classification loss와 함께 최적화

최종 Loss function

\(\mathcal{L}{\text{total}} = \mathcal{L}{\text{cls}} + \lambda \cdot \mathcal{L}_{\text{distill}}\).

• \(\mathcal{L}_{\text{cls}}\): 현재 task의 classification loss
• \(\mathcal{L}_{\text{distill}}\): feature 유지용 loss
• \(\lambda\): distillation 강도 (보통 1)

장점

• 추가 param 없이 이전 모델만 복사하면 됨
• NCM classifier의 정확도 유지에 매우 중요
• ER류 방법과 같이 사용할 수 있음

단점

• 완벽한 유지 불가능: 일정 수준의 drift는 불가피
• 모델 크기가 커질수록 과거 모델 복사 메모리 부담

Code

# f: 현재 모델, f_old: 복사해둔 이전 모델
features_current = f(x)
with torch.no_grad():
    features_old = f_old(x)

loss_distill = F.mse_loss(features_current, features_old)
loss_total = loss_cls + lambda_ * loss_distill

(4) Procedure

1. Task \(t\)의 class 데이터로 모델 학습
2. Feature distillation으로 과거 representation 유지
3. Exemplar memory 업데이트 (herding 방식)
4. 테스트 시에는 NCM 기반 분류기 사용

(5) Pros & Cons

Pros

• Class-Incremental 환경에서 효과적으로 동작
• Task ID 없이도 구분 가능 (non-task-aware)
• Distillation + memory의 결합으로 forgetting 방지

Cons

• 메모리의 class 불균형 가능성
• class 수 많아지면 exemplar 수가 작아져 성능 저하

• feature가 고정되므로 representation drift가 생기면 성능 떨어짐

• 크기 K가 정해져 있을 때,
• class 수가 늘어날수록 class당 exemplar 수 m = \lfloor K / t \rfloor는 줄어듬