(참고: Fastcampus 강의, 강민철의 인공지능 시대 필수 컴퓨터 공학 지식)
3. 컴퓨터 구조 - 데이터
Contents
- 이진수와 2의 보수법
- 부동 소수점
- 문자 인코딩과 디코딩
(1) 이진수와 2의 보수법
컴퓨터는 0&1밖에 이해 못함
모든 양수/음수/소수/문자를 0과 1로 표현하는 방법?
- 양수 = 이진수
- 음수 = 2의 보수
- 소수 = 부동 소수점
- 문자 = 문자 집합 & 인코딩
16 진수
- 1~9 + A~F로 총 16가지 표현

2의 보수법
- 0과 1만으로 음수를 표현
- 2의 보수는 해당 수를 기준으로 가장 크지 않은 2의 배수에서 빼는 것
- How? 모든 0과1을 뒤집은 뒤, 1을 더하기
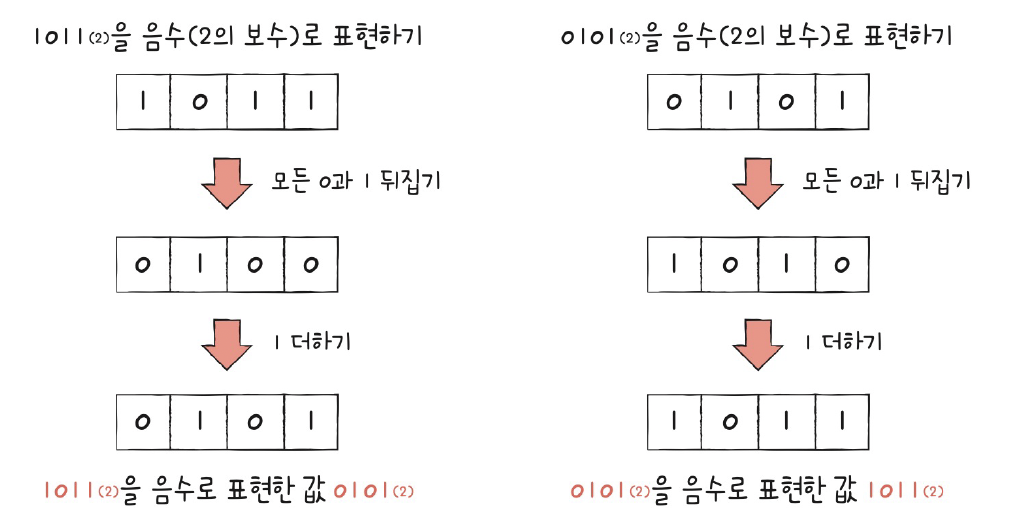
Question) 양수/음수 어떻게 구분?
- CPU 내부의 정보, 플래그(flag)!
• 플래그: CPU가 명령어를 실행하는 과정에서 참고할 정보의 모음
- 음수 플래그가 세팅 O/X: 음수/양수
(2) 부동 소수점
컴퓨터 내의 소수점 표현 방식 = “부동 소수점”
Example) 123.123 십진수를 \(m \times 10^n\) 꼴로 나타내는 법
( \(n\): 지수(exponent), \(m\): 가수(significand) )
- 후보 1) \(1.23123 \times 10^2\)
-
후보 2) \(1231.23 \times 10^{-1}\)
- 후보가 매우 많다!
통일된 형식: 가수부분 \(m\)은 \(1.xxx\)로 하자! (IEEE 754)
-
이럴 경우, \(1\) 이후의 \(xxx\) 부분만 저장하면 됨!
-
ex) \(1101011.1010101\) 이진수를 \(m \times 2^n\) 꼴로 나타낸다고 하면..
\(\rightarrow\) \(1.1010111010101 \times 2^6\) 로 표현
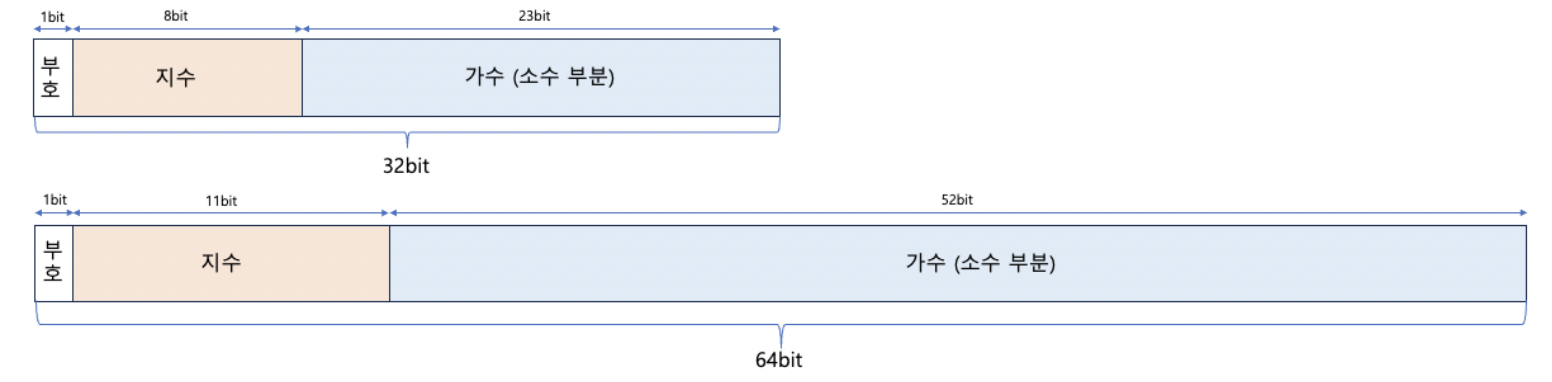
32,64 bit
- 32 bit = 1 bit (부호) + 8 bit (지수) + 23 bit (가수)
- 64 bit = 1 bit (부호) + 11 bit (지수) + 52 bit (가수)
가수 부분 \(m\) 설명
- bias 값이 더해져 저장됨.
- 더해지는 bias 값 = \(2^{k-1}-1\) , where \(k\)=지수의 비트 수
- 32 bit의 경우, \(k=8\)
- 64 bit의 경우, \(k=11\)
0.1+0.2!=0.3인 이유?
- 10진수 소수를 2진수로 표현할 떄, 딱 나눠떨어지지 않을 수 있으므로!
(3) 문자 인코딩과 디코딩
0과 1로 문자 표현하기
- 문자 집합 = 표현
- 문자 encoding = 문자 \(\rightarrow\) (0,1로 이루어진) 문자 코드로
- 문자 decoding = (0,1로 이루어진) 문자 코드로 \(\rightarrow\) 문자
다양한 종류
- 아스키 문자 집합: 영어 위주
- 유니코드 문자 집합: 더 다양함

