( 참고 : 패스트 캠퍼스 , 한번에 끝내는 컴퓨터비전 초격차 패키지 )
Image Clustering
(1) Mahalanobis Distance
Euclidean vs Mahalanobis Distance
Example )
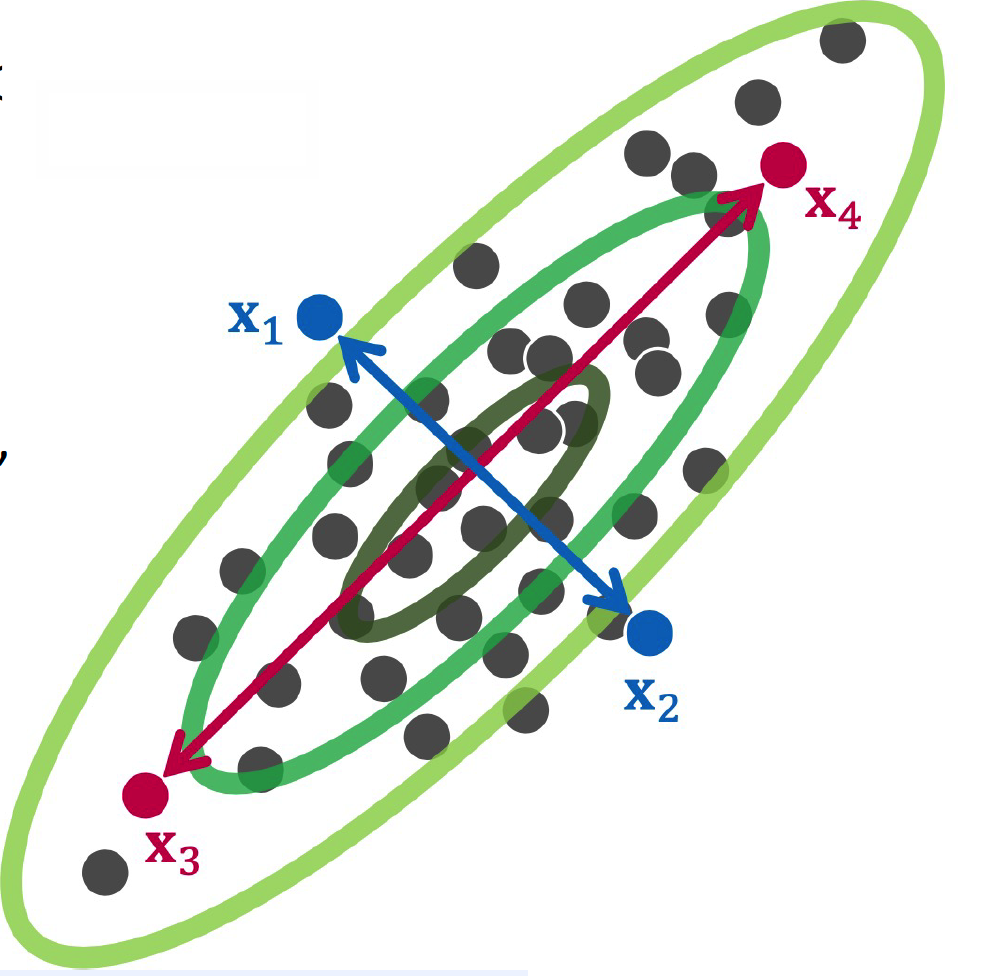
Euclidean : \(D_{E}\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right) < D_{E}\left(\boldsymbol{x}_{3}, \boldsymbol{x}_{4}\right)\)
- \(D_{E}\left(x_{i}, x_{j}\right)=\sqrt{\left(x_{i}-x_{j}\right)^{\top}\left(x_{i}-x_{j}\right)}\).
Mahalanobis : \(D_{M}\left(x_{1}, x_{2}\right)>D_{M}\left(x_{3}, x_{4}\right)\)
- \(D_{M}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\sqrt{\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{\boldsymbol{j}}\right)^{\top} M\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{\boldsymbol{j}}\right)}\).
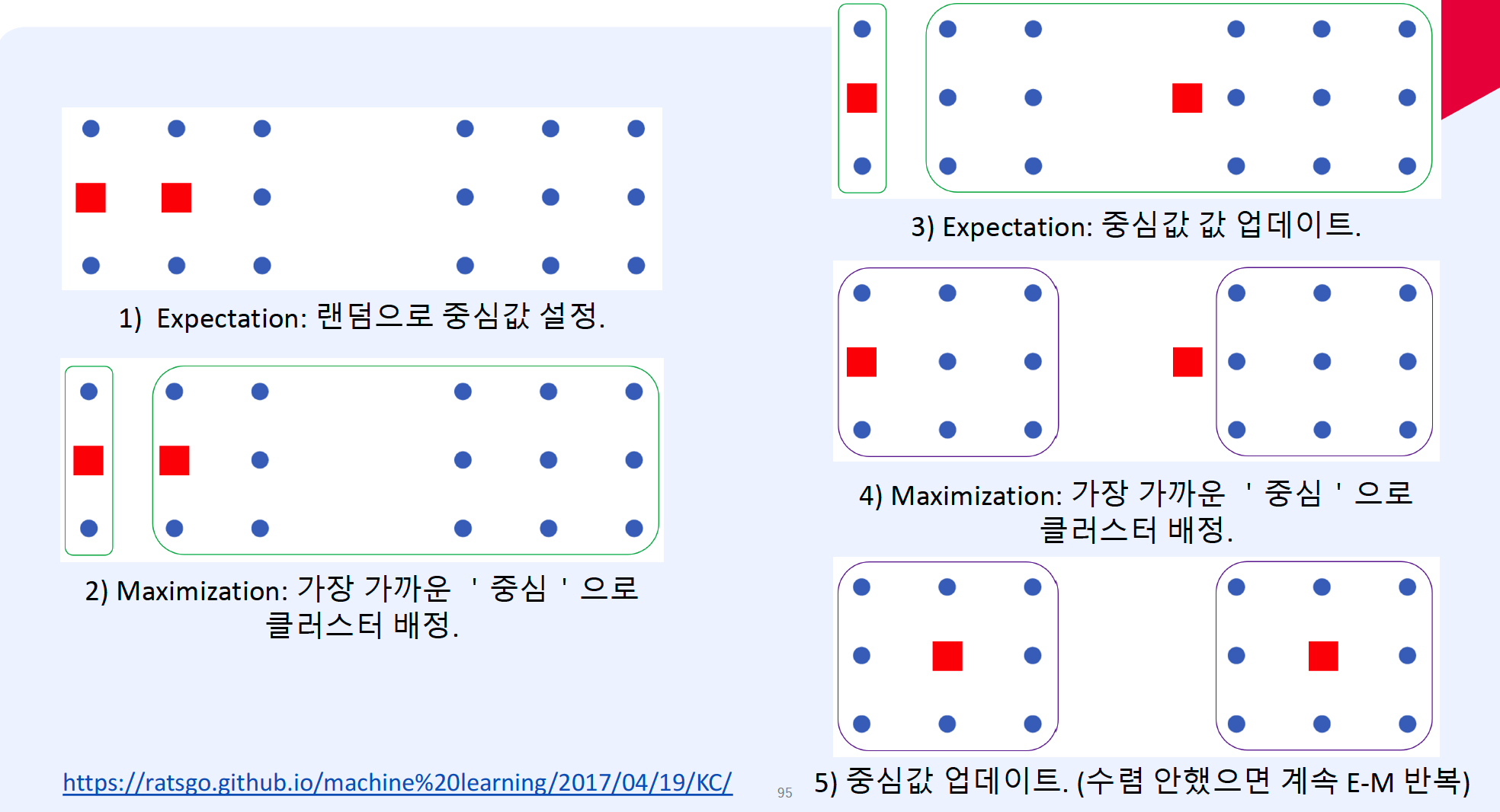
(2) K-means Clustering
- clustering based on centroid
- framework : EM algorithm
- E step : finding centroid
- M step : assigning data to centroids
\(\begin{gathered} X=C_{1} \cup C_{2} \ldots \cup C_{K}, \quad C_{i} \cap C_{j}=\phi \\ \operatorname{argmin}_{C} \sum_{i=1}^{K} \sum_{x_{j} \in C_{i}} \mid \mid x_{j}-c_{i} \mid \mid ^{2} \end{gathered}\).
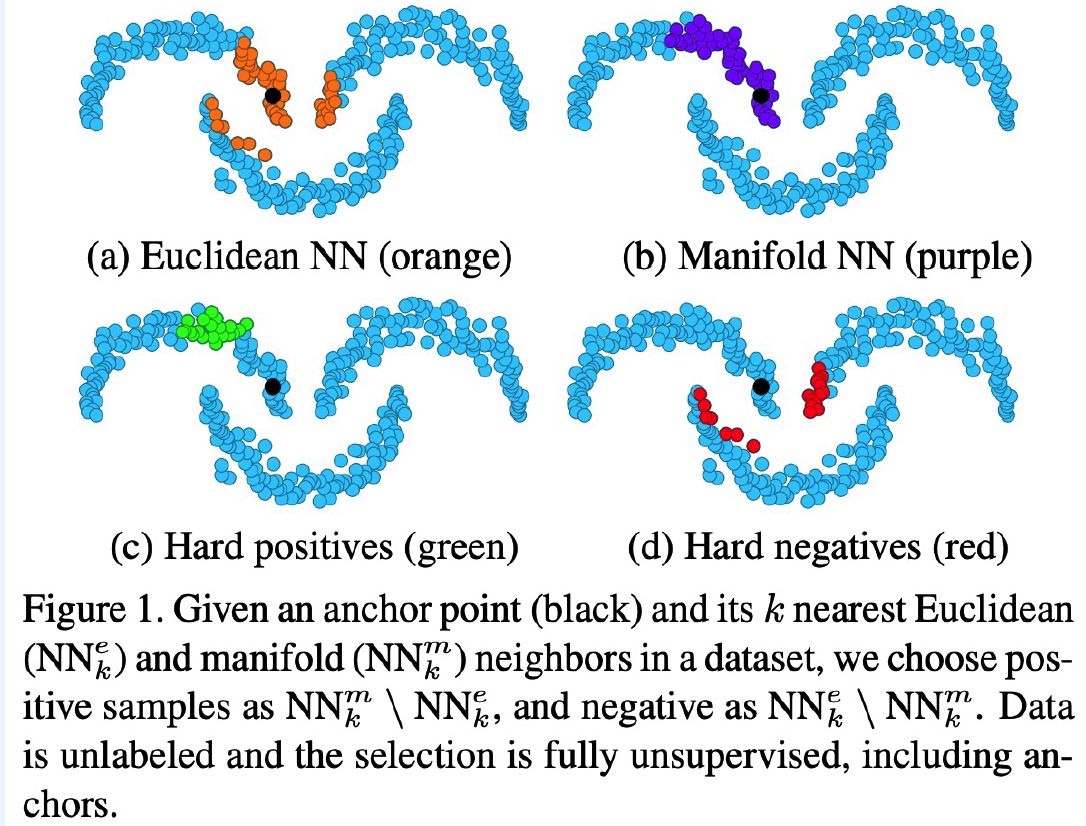
(3) Unsupervised Metric Learning
Why not find embedding space, using metric learning w.o labeled data?
( + previous supervised metric learning may cause overfitting! )
Solution
- step 1) pre-train with UN-labeled images
- contrastive learning, using hard positives & hard negatives in manifold
- step 2) fine-tune with labeled images
Example)
- contrastive loss :
- \(l_{c}\left(\mathbf{z}^{r}, \mathbf{z}^{+}, \mathbf{z}^{-}\right)= \mid \mid \mathbf{z}^{r}-\mathbf{z}^{+} \mid \mid ^{2}+\left[m- \mid \mid \mathbf{z}^{r}-\mathbf{z}^{-} \mid \mid _{+}^{2}\right]\).
- triplet loss :
- \(l_{t}\left(\mathbf{z}^{r}, \mathbf{z}^{+}, \mathbf{z}^{-}\right)=\left[m+ \mid \mid \mathbf{z}^{r}-\mathbf{z}^{+} \mid \mid ^{2}- \mid \mid \mathbf{z}^{r}-\mathbf{z}^{-} \mid \mid \right]_{+}^{2}\).
Ground Truth (O)

Ground Truth (X)

Conclusion
- without discrete category label, use fine-grained similarity
- save annotation cost!
- cons :
- still need some pre-trained model!
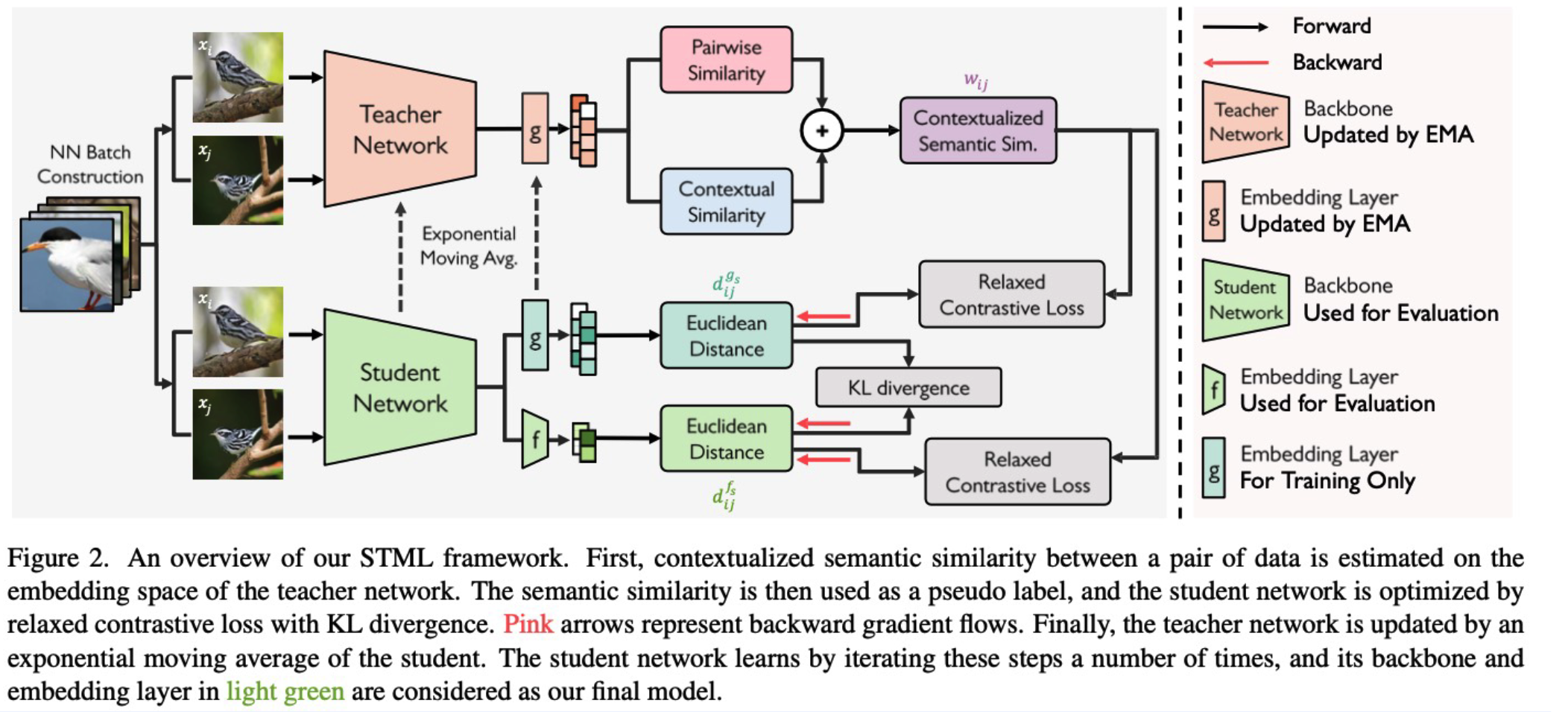
Self-Taught Metric Learning without Labels ( Kim et al., CVPR 2022 )
use Pseudo-label!
\(\rightarrow\) solution : self-taught networks ( by self-knowledge distillation )
(4) t-SNE
t-SNE
= t-distributed Stochastic Neighbor Embedding
( dimension reduction for visualization of high-dim data )
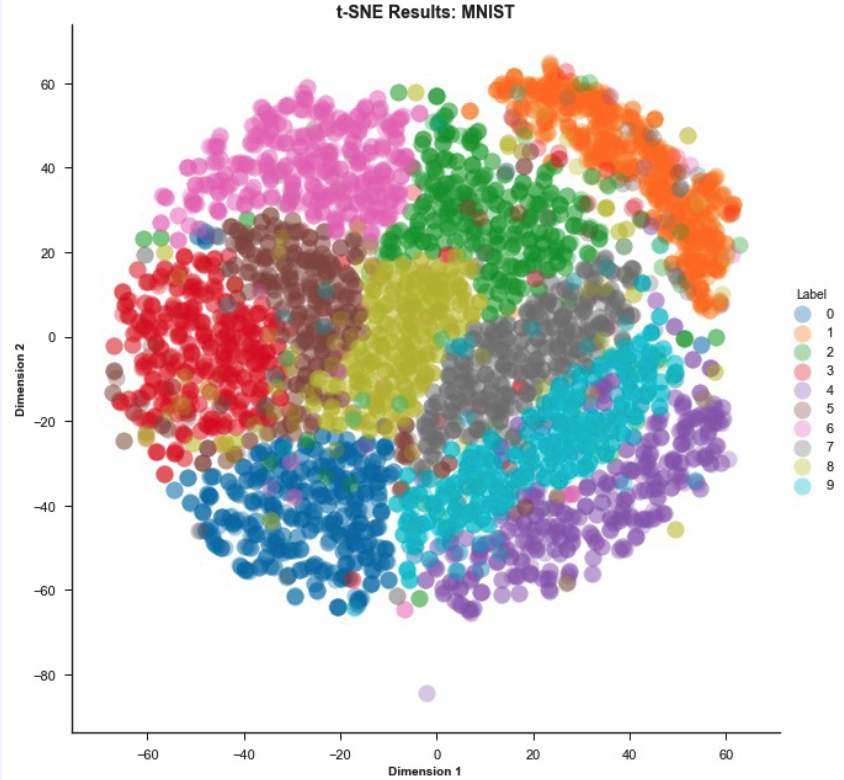
( for more details, refer to https://seunghan96.github.io/ml/stat/t-SNE/ )
