(paper) Few-shot Learning for Time Series Forecasting

Few-shot Learning for Time Series Forecasting

Contents

1. Abstract
2. Introduction
   1. Problem formuation
3. Method
   1. Architecture
   2. Training procedure
   3. Test

0. Abstract

propose a few-shot learning method that …

• forecasts a future value of a TS in a target task,

  given a few TS in the target tasks

model

• trained using TS data in multiple training tasks, that are different from target tasks
• build a function based on (1) RNN & (2) attention mechanism

1. Introduction

(1) Problem formuation

• TS in the target task are not given in training phase

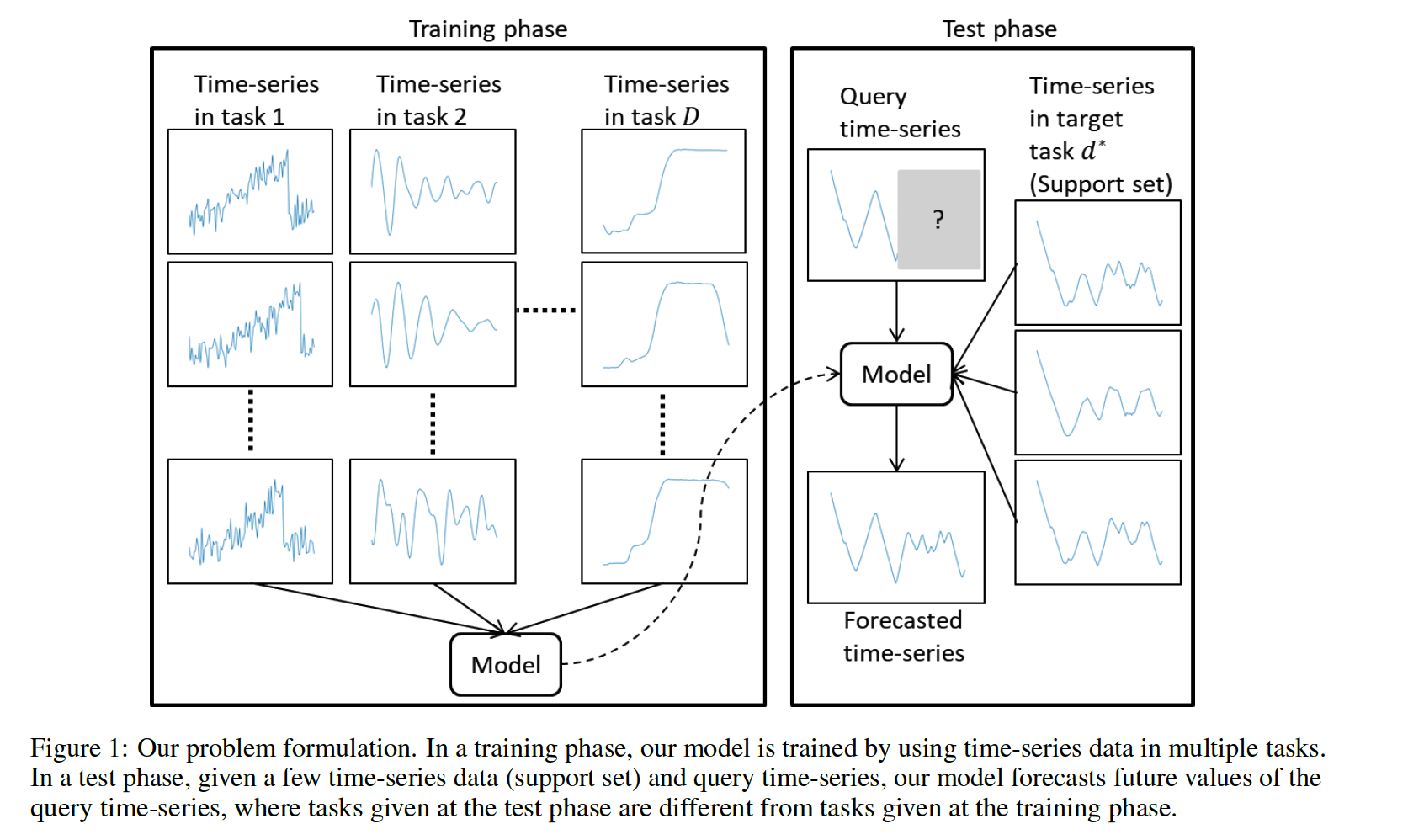
Given a few TS ( = support set ),

proposed model outputs a value at the next time-step of TS ( = query )

step 1) obtain representations of support set with bi-LSTM

step 2) forecast future values of query, considering the support representations

2. Method

(1) Architecture

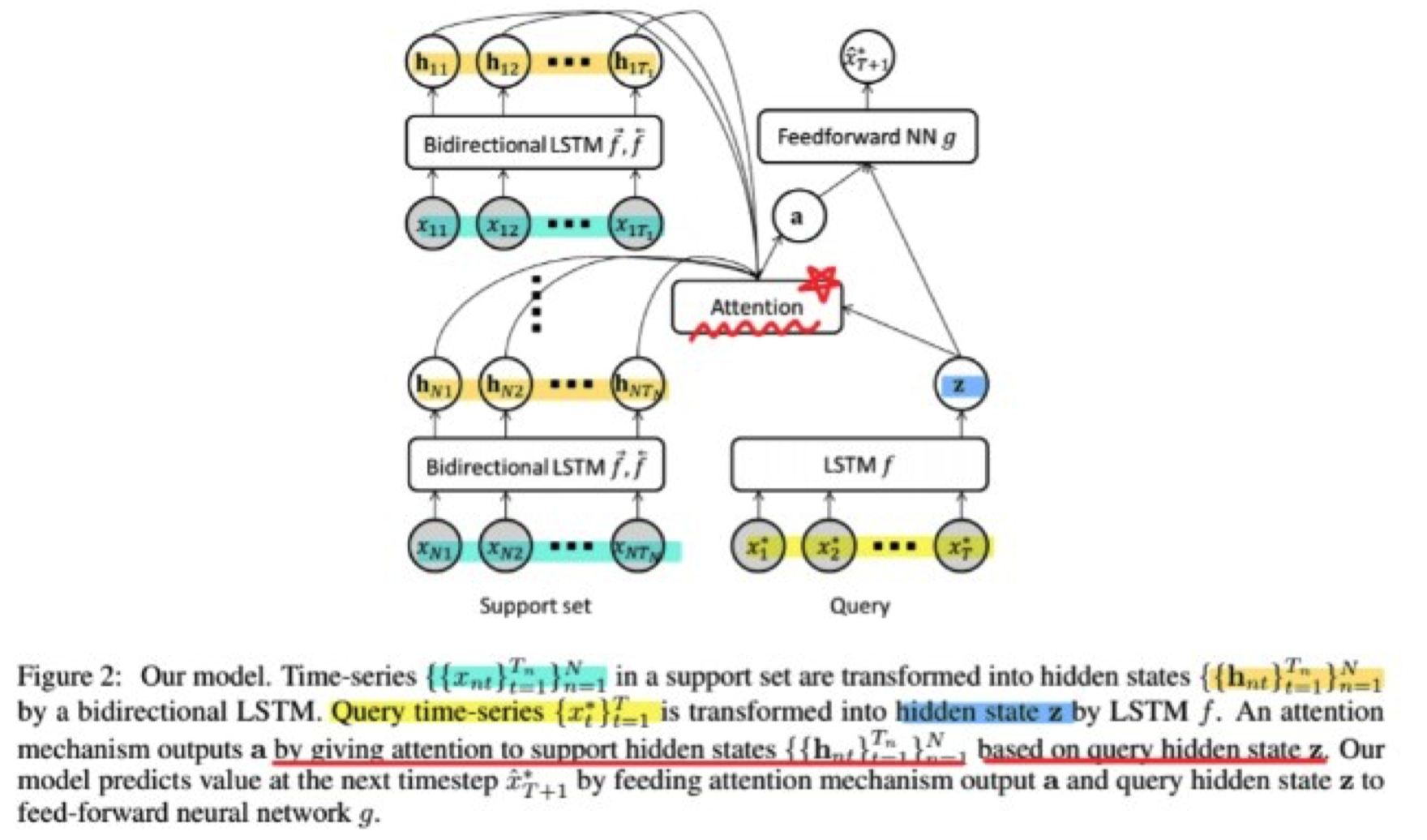
\(\mu\left(\mathbf{x}^* ; \mathcal{S}, \boldsymbol{\Phi}\right):=g([\mathbf{a}, \mathbf{z}])\).

• forecast a value at next timestep \(t+1\), using both..
  • (1) attention output \(\mathbf{a}\)
  • (2) query representation \(\mathbf{z}\)

(2) Training procedure

Notation

• 1d TS in \(\mid \mathcal{D} \mid\) tasks \(\mathcal{X}=\left\{\mathbf{X}_d\right\}_{d \in \mathcal{D}}\),
  • where \(\mathbf{X}_d=\) \(\left\{\mathbf{x}_{d n}\right\}_{n=1}^{N_d}\) is the set of TS in task \(d\)
    • \(\mathbf{x}_{d n}=\left[x_{d n 1}, \ldots, x_{d n T_{d n}}\right]\) : \(n\)-th TS in task \(d\)
      • \(T_{d n}\) : length of TS in task \(d\)
      • \(N_d\) : number of TS in task \(d\)

Optimization : minimize the expected loss on query set

\(\hat{\boldsymbol{\Phi}}=\arg \min _{\boldsymbol{\Phi}} \mathbb{E}_{d \sim \mathcal{D}}\left[\mathbb{E}_{(\mathcal{S}, \mathcal{Q}) \sim \mathbf{X}_d}[L(\mathcal{S}, \mathcal{Q} ; \boldsymbol{\Phi})]\right]\).

• \(L(\mathcal{S}, \mathcal{Q} ; \boldsymbol{\Phi})=\frac{1}{N_{\mathrm{Q}}} \sum_{n=1}^{N_{\mathrm{Q}}} \frac{1}{T_n} \sum_{t=1}^{T_n} \mid \mid \mu\left(\mathbf{x}_{n, t-1}, \mathcal{S} ; \boldsymbol{\Phi}\right)-x_{n t} \mid \mid ^2\).

(3) Test

given a few TS in a new task \(d^{*} \notin \mathcal{D}\) as a support set