(paper) Transfer Learning with Time Series Data ; A Systemetic Mapping Study

Transfer Learning with Time Series Data : A Systemetic Mapping Study

Contents

1. Abstract
2. Overview & Definitions
   1. Time Series (TS)
   2. TS problems
   3. Transfer Learning
   4. TL solution approachs

0. Abstract

Transfer Learning (TL) :

• relaxes the assumption that train & test data need to be drawn from same distn
• benefits from various TS domains

conduct a study of literature on TL with TS data

1. Overview & Definitions

(1) Time Series (TS)

• Time Series : \(T=\left[x_1, \ldots, x_n\right]\)
  • data points \(x_i\) of length \(n\)
• Uni & Multi-variate TS
  • Univariate : TS where \(x_i \in \mathbb{R}\).
  • Multivariate : TS where each \(x_i\) is a d-dim vector of real values \(\left(x_i^1, \ldots, x_i^d\right), x_i^j \in \mathbb{R}\).

(2) TS problems

1. TS classification

   • Assign a TS ( or subsequence TS ) a class \(c_i\), out of \(C=\left\{c_1, \ldots, c_n \mid n \geq 2\right\}\)

2. TS regression

   • For TS \(T\), predict numeric value (\(y\)) / values (\(y_1, \ldots, y_n\))

3. TS clustering

   • Assign a TS ( or subsequence TS ) a cluster \(c_i\), out of \(C=\left\{c_1\right. \left.\ldots, c_n \mid n \geq 1\right\}\)

     based on similarity measure \(\operatorname{Sim}(a, b)\)

4. TS anomaly detection

   • Assign a TS ( or subsequence TS ) to one of \(\left\{c_{\text {normal }}, c_{\text {anomaly }}\right\}\)

5. TS forecasting

   • Given \(T=\left[x_1, \ldots, x_n\right]\), predict..
     • (1) single-step : \(x_{n+1}\)
     • (2) multi-step : \(x_{n+1}, \ldots, x_{n+m}\)

(3) Transfer Learning

• transfer knowledge from one domain to another simliar domain

• to improve the generalization ability

Notation

• (SOURCE) domain

  • source domain : \(D_S\)
  • source domain learning task : \(T_S\)
  • model : \(f_S(\cdot)\)

• (TARGET) domain

  • target domain : \(D_T\)
  • target domain learning task : \(T_T\)
  • model : \(f_T(\cdot)\)

• Goal : improve \(f_T(\cdot)\) using the knowledge in \(D_S\) & \(T_S\) ,

  where \(D_S \neq D_T\) or \(T_S \neq T_T\)

Types of TL

• (1) Domain Adaptation : \(D_S \neq D_T\)
• (2) Task Adaptation : \(T_S \neq T_T\)
• Combination = (1) + (2)

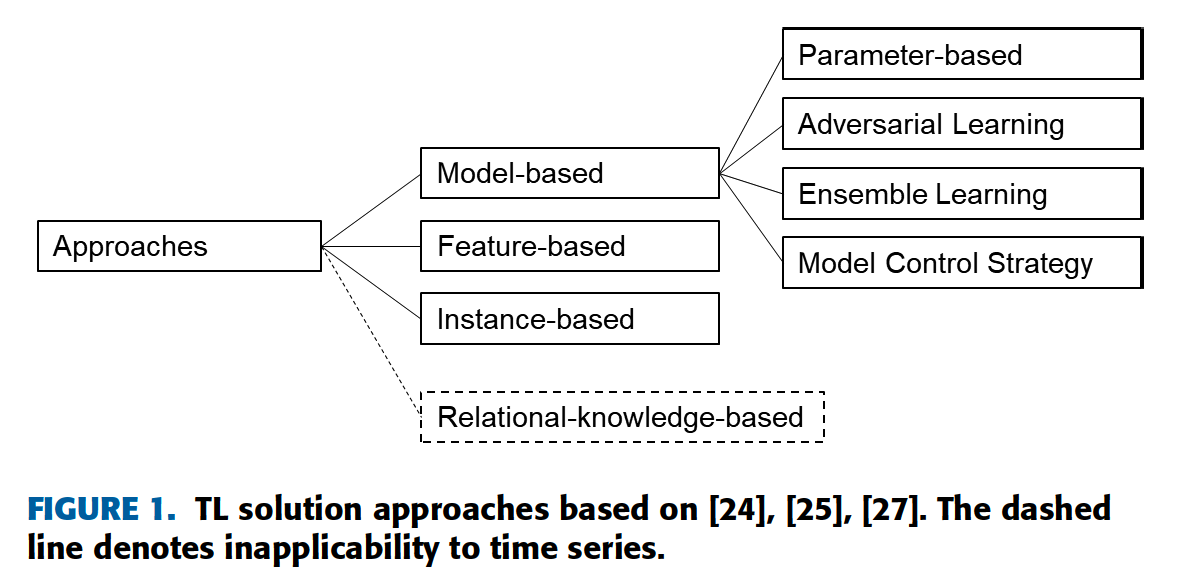
(4) TL solution approachs

1. instance-based

   • selection or reweighting of samples from the source domain
   • assumption ) instance from source domain are more/less similar to the set of target domain instances

2. feature-representation-based ( = mapping-based )

   • map into common feature space

     ( place of features, representating characteristics of both domains )

3. parameter-based ( = network transfer )

   • use pre-trained model

4. relational-knowledge-based

   • not applicable to TS