(paper) Reconstruction and Regression Loss for TS Transfer Learning

Reconstruction and Regression Loss for TS Transfer Learning

Contents

1. Abstract
2. Transfer Learning in TS
   1. Model Loss & Architecture

0. Abstract

Define a new architecture & new loss function for TS Transfer Learning

1. Transfer Learning in TS

Notation

• domain \(D\) consists of..
  • marginal pdf \(P(X)\) over the feature space \(X=\left\{x_1, \ldots, x_n\right\}\)
• task \(T\) : given \(\mathcal{D}=\{\mathcal{X}, P(\mathcal{X})\}\) , model \(P(Y \mid X)\)
• source / traget domain
  • source domain : \(\mathcal{D}_S\)
  • source task : \(\mathcal{T}_S\)
  • target domain : \(\mathcal{D}_T\)
  • target task : \(\mathcal{T}_T\)

\(\rightarrow\) TL aims to learn the target conditional pdf \(P\left(Y_T \mid X_T\right)\) in \(\mathcal{D}_T\) , from the information learned from \(\mathcal{D}_S\) and \(\mathcal{T}_T\).

Traditional TS decomposition :

• TS = Trend + Seasonality + Residual

\(\rightarrow\) instead of defining explicit model components, LSTM model only consists of 5 different non-linear components

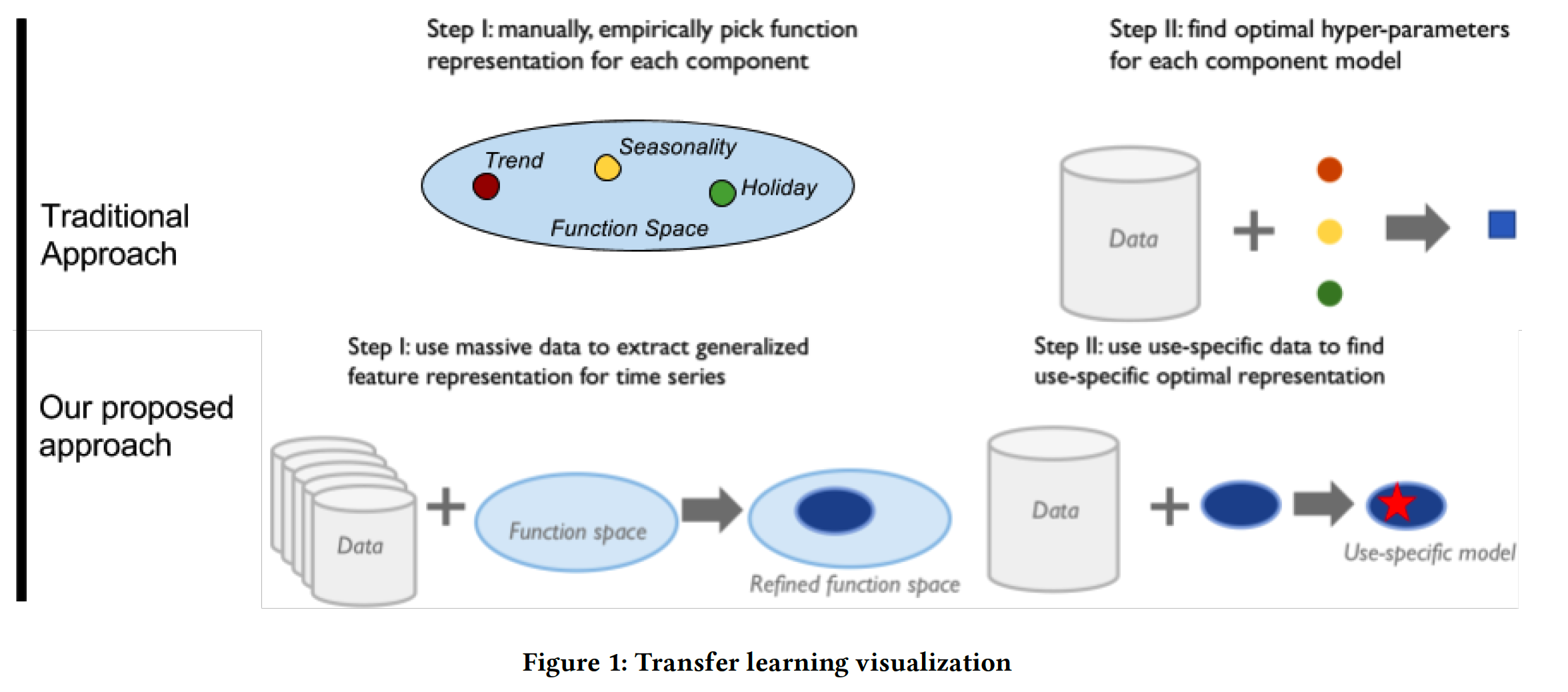
decompose model into 2 types of layers

• (1) feature layers
• (2) predictive layers

After model training….

• a set of feature layers is typically frozen
• predictive layers are re-trained

(1) Model Loss & Architecture

Loss functions

• (1) Regression loss : simple MSE loss
• (2) Reconstruction loss : \(\mathbb{E}_{q_\phi(z \mid x)}\left[\log p_\theta(x \mid z)\right]\)

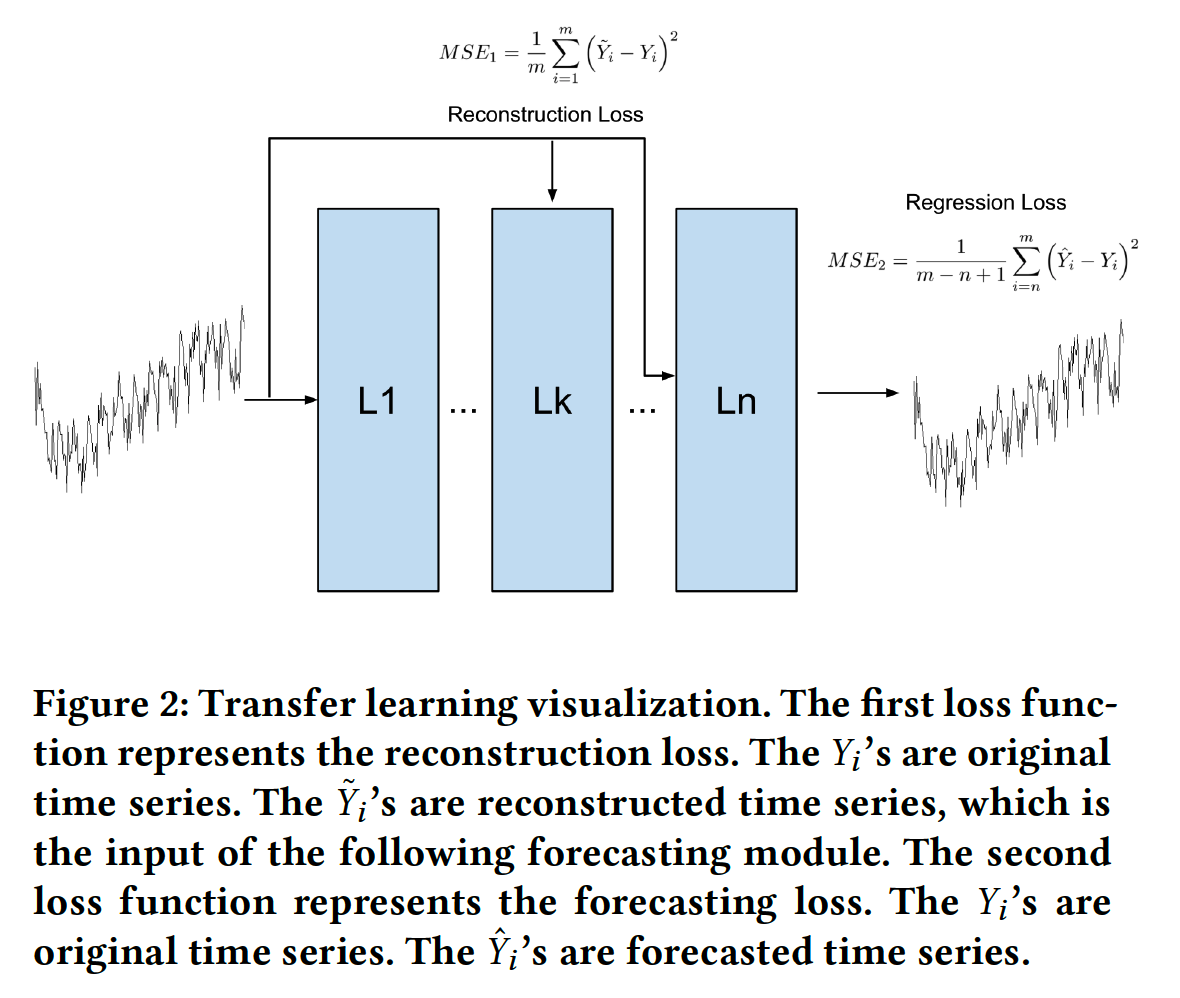
• (L1) FC layer ( extract TS features )
• (L2) Bottleneck layer ( reconstruction loss is computed )
• (L3) set of LSTM layers
  • input : output of FC layer & originla input
  • perform prediction & compte forecasting loss

\(\rightarrow\) optimize both losses jointly