CGAN (Conditional GAN)
1. Introduction
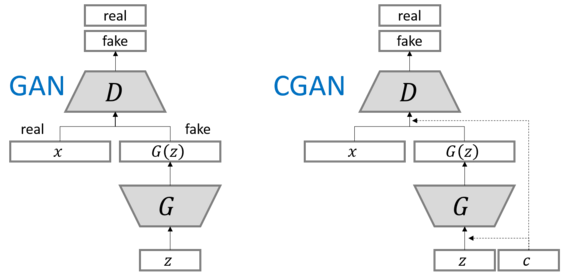
CGAN도 GAN의 일종으로, 기존의 GAN과의 차이점은 바로 “Generator와 Discriminator에 특정한 조건”을 요구한다는 점이다. MNIST 데이터를 예로 들면, Generator의 input에 noise만을 주는 것이 아니라, 원하는 숫자를 One-Hot Encoding한 벡터를 함께 입력으로 넣는다. 그러면 Generator는 이 2개의 input으로, 요구받은 숫자의 사진을 만들도록 노력한다. 다음 그림을 통해 쉽게 이해할 수 있을 것이다.
https://nooverfit.com/wp/wp-content/uploads/2017/10/Screenshot-from-2017-10-07-120039.png
( 위 그림에서 ‘c’는 One-Hot Encoding된 숫자 벡터다 )
2. CGAN의 원리
위처럼 ‘조건이 부여’된다는 점을 제외하면 CGAN도 GAN과 동일하다. 그렇다면, CGAN의 loss function은 어떻게 달라질까?
Loss Function of Discriminator
\(L^{(D)}(\theta^{(G)},\theta^{(D)})\) = \(-E_{x \sim P_{data}}logD(x \mid y)\) \(-E_{z}log(1-D(G(z\mid y')\mid y'))\)
- y’ : Generator에 입력된 One-Hot Label
- y : Discriminator에 입력된 One-Hot Label
위 식을 약간 정리하면 다음과 같이 나타낼 수 있다.
\(L^{(D)}(\theta^{(G)},\theta^{(D)})\) = \(-E_{x \sim P_{data}}logD(x \mid y)\) \(-E_{z}log(1-D(G(z\mid y')))\)
Loss Function of Generator
GAN에서도 봤듯, Generator의 Loss Function은 Discrimnator 것의 (-) 부호에다가, Generator오는 관계없는 부분을 제외하면 된다.
\(L^{(G)}(\theta^{(G)},\theta^{(D)})\) = \(-E_{z}log(D(G(z\mid y')))\)
3. Conclusion
지금 까지 GAN과 CGAN에 대해서 알아봤다. 한 마디로 요약하자면, Generator와 Discriminator간의 경쟁 구조를 통해 진짜와 유사한 이미지를 만들어내는 Generator를 생성해낼 수 있다. 다음 포스트에서는 새로운 Loss Function을 도입하여 성능을 더 높힌 GAN의 다양한 모델들에 대해서 더 알아볼 것이다.
