8.Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddins (2016)
목차
- Abstract
- Introduction
- Preliminaries
- Gender stereotypes in word embeddings
- Geometry of Gender and Bias
- Identifying the gender subspace
- Direct bias
- Indirect bias
- Debiasing algorithms
Abstract
word embeddings show female/male gender stereotypes!
provide a method for modifying an embedding to remove gender stereotypes
1. Introduction
Word embedding catpures word’s meaning!
- ex) \(\overrightarrow{\operatorname{man}}-\overrightarrow{\operatorname{woman}} \approx \overrightarrow{\mathrm{king}}-\overrightarrow{\text { queen }}\).
But..also have sexism implicit!
- ex) \(\overrightarrow{\operatorname{man}}-\overrightarrow{\text { woman }} \approx \overrightarrow{\text { computer programmer }}-\overrightarrow{\text { homemaker }}\).
This paper..
- shows that “word-embeddings contain biases”
- not only reflects such stereotypes, but also amplify them!
1) To quantify bias, compare a word embedding to the embeddings of a pair of gender-specific words!
- ex) nurse vs man & nurse vs woman
2) Use gender specific words to learn gender subspace in the embedding
3) Debiasing algorithm removes the bias only from the gender neutral words!
- ( still respect the definitions of gender specific words, such as “he”,”she”…..)
4) consider notion of INDIRECT bias
- ex) ‘receptionist’ is closer to ‘softball’ than ‘football’
Goals of debiasing
- (1) Reduce bias
- (2) Maintain embedding utility
2. Preliminaries
notation
- \(\vec{w} \in \mathbb{R}^{d}\) : embedding of each word, where \(w \in W\)
- \(N \subset W\) : set of “gender neutral” words
- \(\mid S\mid\) : size of set \(S\)
- \(P \subset W \times W\) : female-male gender pairs
- ex) she-he, mother-father
- \(\cos (u, v)=\frac{u \cdot v}{ \mid \mid u \mid \mid \mid \mid v \mid \mid }\).
- similarity between two words are measured by inner product!
Embedding
- \(d=300\) dim word2vec embedding
Crowd Experiments
- 2 types of experiments
- 1) solicited words from the crowd
- 2) solicited ratings on words, or analogies generated from our embedding
- ( since gender association vary by culture&person, ask for ratings of stereotypes rather than bias )
3. Gender stereotypes in word embeddings
Task 1 ) Understand the bias in embeddings
- 2 simple methods :
- 1) evaluate whether the embedding has stereotypes on occupation words
- 2) evaluate whether the embedding produces analogies that are judged to reflect stereotypes by humans
(1) Occupational stereotypes

- asked the crowds to evaluate (a) female-stereotypic, (b) male-stereotypic, (c) neutral
- 10 people per word ( thus, rating on a scale of 0~10 )
- projected each occupations onto the she-he direction
(2) Analogies exhibiting stereotypes
- standard analogy task : he : she = king : x
- modification : he : she = x : y
- generate pairs of words that the embedding believes it analogous to he, she
- score all pairs of words x,y
- \(\mathrm{S}_{(a, b)}(x, y)=\left\{\begin{array}{ll} \cos (\vec{a}-\vec{b}, \vec{x}-\vec{y}) & \text { if } \mid \mid \vec{x}-\vec{y} \mid \mid \leq \delta \\ 0 & \text { otherwise } \end{array}\right.\).
- \(\delta\) : threshold for similarity
- ex) \(a\) : he, \(b\) : she
(3) Indirect gender bias
- gender bias could also affect the relative geometry between gender neutral words themselves
- ex) bookkeeper & receptionists are much closer to softball than football
4. Geometry of Gender and Bias
4-1. Identifying the gender subspace
By combining several directions, identify a gender direction \(g \in \mathbb{R}^{d}\)
- ex) \(\overrightarrow{\mathrm{she}}-\overrightarrow{\mathrm{he}}\)
Gender pair differences are not parallel in practice! Reason?
- 1) different biases associated!
- 2) polysemy (?)
- 3) randomness in the word counts in any finite sample
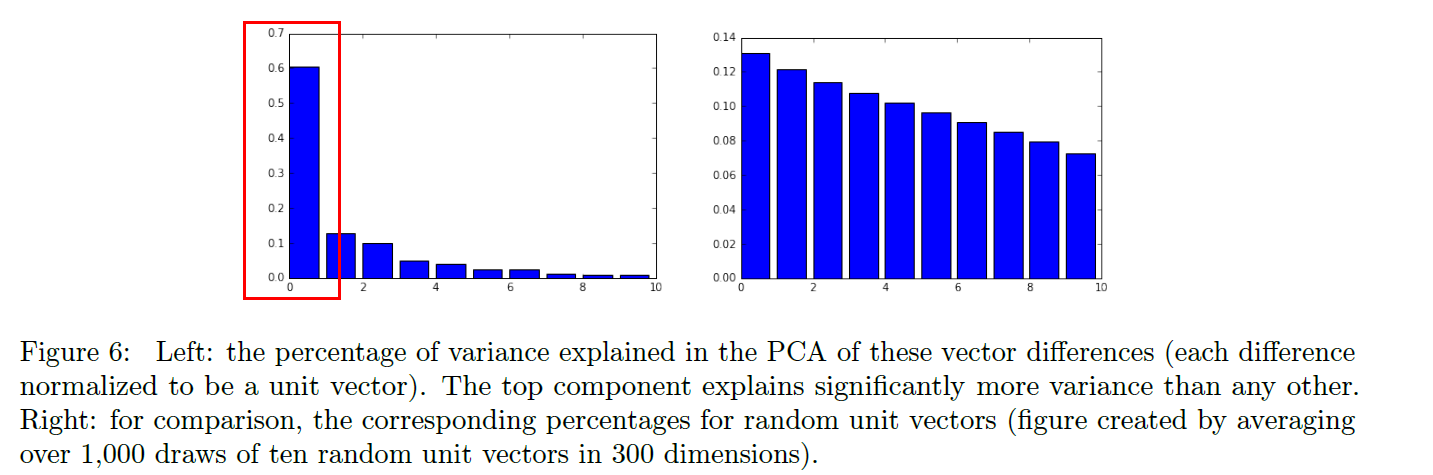
Use PCA to identify gender subspace! can see that there is a single direction that explains the majority of variance in these vectors
4-2. Direct bias
to measure direct-bias, identify words that should be gender-neutral
- gender neutral words : \(N\)
- gender direction ( learned above ) : \(g\)
direct gender bias :
-
$$\text { DirectBias }_{c}=\frac{1}{ N } \sum_{w \in N} \cos (\vec{w}, g) ^{c}$$. ( \(c\) : parameter that determines how strict do we want to in measuring bias )
4-3. Indirect bias
decompose a given word vector \(w \in \mathbb{R}^{d}\) : \(w=w_{g}+w_{\perp}\)
-
\(w_{g}=(w \cdot g) g\) : contribution from gender
-
gender component :
\[\beta(w, v)=\left(w \cdot v-\frac{w_{\perp} \cdot v_{\perp}}{\left \mid \mid w_{\perp}\right \mid \mid _{2}\left \mid \mid v_{\perp}\right \mid \mid _{2}}\right) / w \cdot v\]- quantifies how much this inner product changes, due to this operation of removing the gender subspace.
5. Debiasing algorithms
defined in terms of set of words, rather than just pairs
Step 1) Identify gender subspace
Step 2) Neutralize and Equalize, or Soften
notation :
- dddd : projection of vector \(v\) onto \(B\)
Step 1) Identify gender subspace
-
identify a direction of the embedding that captures bias
-
inputs : word sets \(W\)
-
defining sets : \(D_{1}, D_{2}, \ldots, D_{n} \subset W\)
-
means of the defining sets : $$\mu_{i}:=\sum_{w \in D_{i}} \vec{w} /\left D_{i}\right $$ -
bias subspace \(B\) be the first \(k\) rows of \(SVD(\mathbf{C})\)
where $$\mathbf{C}:=\sum_{i=1}^{n} \sum_{w \in D_{i}}\left(\vec{w}-\mu_{i}\right)^{T}\left(\vec{w}-\mu_{i}\right) /\left D_{i}\right $$
Step 2a) Neutralize and Equalize, or Soften
-
Neutralize : ensures that “gender neutral words are zero” in gender subspace
-
Equalize : equalizes sets of words outside the subspace
-
inputs : words to neutralize \(N \subseteq W\) & family of equality sets \(\mathcal{E}=\left\{E_{1}, E_{2}, \ldots, E_{m}\right\}\)
( where each \(E_{i} \subseteq W\) )
-
(words to neutralize) re-embedded : \(\vec{w}:=\left(\vec{w}-\vec{w}_{B}\right) /\left \mid \mid \vec{w}-\vec{w}_{B}\right \mid \mid\)
-
for each set \(E \in \mathcal{E}\),
\(\begin{aligned} &\mu :=\sum_{w \in E} w /|E| \\ &\nu :=\mu-\mu_{B} \\ &\text { For each } w \in E, \quad \vec{w} :=\nu+\sqrt{1- \mid \mid \nu \mid \mid ^{2}} \frac{\vec{w}_{B}-\mu_{B}}{\left \mid \mid \vec{w}_{B}-\mu_{B}\right \mid \mid } \end{aligned}\)>
-
output the subspace \(B\) and new embedding \(\left\{\vec{w} \in \mathbb{R}^{d}\right\}_{w \in W}\).
Step 2b) Soft bias correction
- seeks to preserve pairwise inner product between all word vectors,
- while minimizing the projection of the gender neutral words onto the gender subspace
- \(\min _{T}\left \mid \mid (T W)^{T}(T W)-W^{T} W\right \mid \mid _{F}^{2}+\lambda\left \mid \mid (T N)^{T}(T B)\right \mid \mid _{F}^{2}\).
