37.(paper) 9.Adversarial Multi-task Learning for Text Classification

9.Adversarial Multi-task Learning for Text Classification (2017)

목차

1. Abstract
2. Introduction
3. Recurrent Models for Text Classification
   1. LSTM
   2. Text Classification with LSTM
4. Multi-task Learning for Text Classification
   1. Two Sharing Schemes for Sentence Modeling
   2. Task-Specific Output Layer
5. Incorporating Adversarial Training
   1. Adversarial Network
   2. Task Adversarial Loss for MTL
   3. Orthogonality Constraints
   4. Put it all together

Abstract

Multi-task learning : focus on learning the shared layers to extract common and task-invariant features

BUT…prone to be contaminated by task-specific features..

This paper proposes an ADVERSARIAL multi-task learning framework!

• alleviate the “shared” and “private” latent feature spaces from interfering with each other

1. Introduction

Multi-task learning

• efficient approach to improve the performance of “single task” with the help of “other tasks”
• however, modern methods attempts to divide the features of different tasks into private & shared, MERELY based on whether the params of some components should be shared!

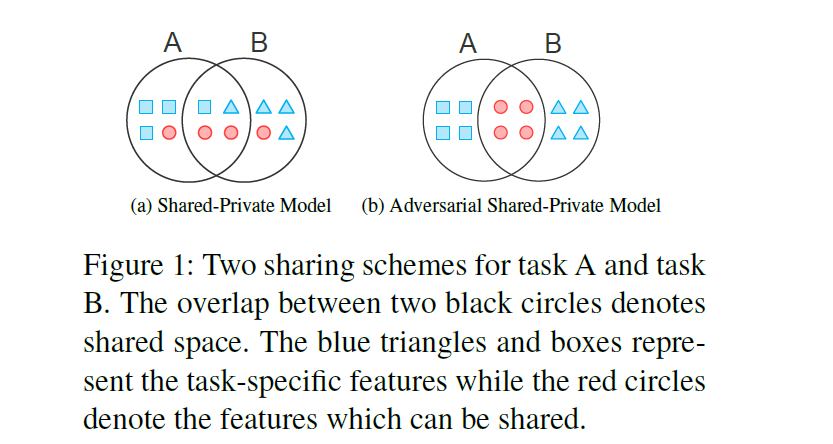
(figure 1-a) Shared-Private model

• 2 feature spaces for any task

  • (space 1) to store task-dependent features

  • (space 2) to capture shared features

• limitation :

  • shared feature space could contain some unnecessary task-specific fatures

  • sharable features could also be mixed in private space

To address this problem, propose ADVERSARIAL multi-task framework

• shared & private feature spaces are inherently disjoint by introducing “orthogonality constraints”

• Introduce 2 strategies

  • 1) adversarial training : to ensure that the shared feature space simply contains common & task-invariation information
  • 2) orthogonality constraints : to eliminate redundant features from the private & shared space

Contribution

• 1) divides task-specific & shared space in a more precise way
• 2) extend binary adversarial training to multi-class
• 3) condense the shared knowledge among multiple tasks

2. Recurrent Models for Text Classification

2-1. LSTM

\(\begin{aligned} \left[\begin{array}{c} \tilde{\mathbf{c}}_{t} \\ \mathbf{o}_{t} \\ \mathbf{i}_{t} \\ \mathbf{f}_{t} \end{array}\right] &=\left[\begin{array}{c} \tanh \\ \sigma \\ \sigma \\ \sigma \end{array}\right]\left(\mathbf{W}_{p}\left[\begin{array}{c} \mathbf{x}_{t} \\ \mathbf{h}_{t-1} \end{array}\right]+\mathbf{b}_{p}\right), \\ \mathbf{c}_{t} &=\tilde{\mathbf{c}}_{t} \odot \mathbf{i}_{t}+\mathbf{c}_{t-1} \odot \mathbf{f}_{t} \\ \mathbf{h}_{t} &=\mathbf{o}_{t} \odot \tanh \left(\mathbf{c}_{t}\right) \end{aligned}\).

• \(\mathbf{x}_{t} \in \mathbb{R}^{e}\) : input at the current time step
• \(\mathbf{W}_{p} \in \mathbb{R}^{4 d \times(d+e)}\) : parameters

Update of each LSTM unit : \(\mathbf{h}_{t}=\mathbf{L S T M}\left(\mathbf{h}_{t-1}, \mathbf{x}_{t}, \theta_{p}\right)\)

2-2. Text Classification with LSTM

\(\hat{\mathbf{y}}=\operatorname{softmax}\left(\mathbf{W} \mathbf{h}_{T}+\mathbf{b}\right)\).

\(L(\hat{y}, y)=-\sum_{i=1}^{N} \sum_{j=1}^{C} y_{i}^{j} \log \left(\hat{y}_{i}^{j}\right)\).

3. Multi-task Learning for Text Classification

goal of multi-task learning : utilizes the correlation among these tasks!

\(D_k\) : dataset with \(N_k\) samples for task \(k\)

\(D_{k}=\left\{\left(x_{i}^{k}, y_{i}^{k}\right)\right\}_{i=1}^{N_{k}}\).

• \(x_{i}^{k}\): sentence
• \(y_{i}^{k}\) : label

3-1. Two Sharing Schemes for Sentence Modeling

Introduce 2 sharing schemes

• 1) fully-shared scheme
• 2) shared-private scheme

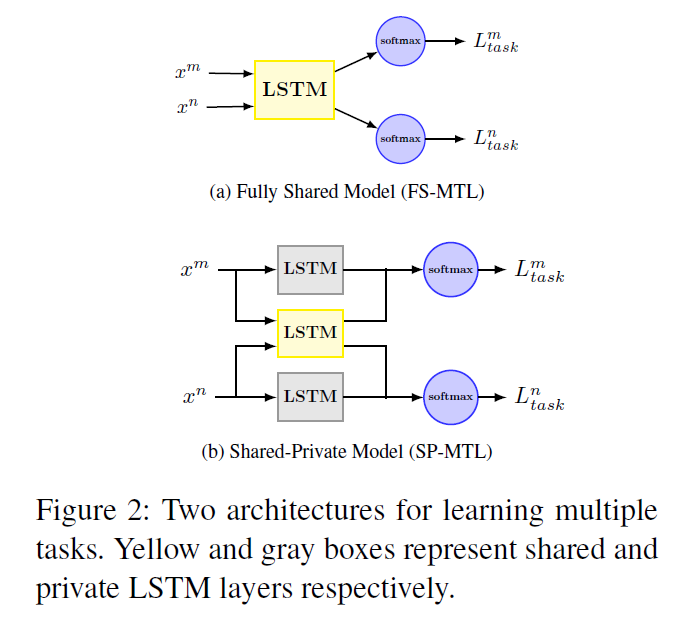
1) Fully-Shared Model (FS-MTL)

• use single shared LSTM layer to extract features for all the tasks

• ignores the fact that some features are task dependent

2) Shared-Private Model (SP-MTL)

• introduce 2 feature spaces for each task

  • 1) task-dependent features
  • 2) task-invariant features

• \(\mathrm{s}_{t}^{k}\): shared representation

• \(\mathbf{h}_{t}^{k}\): task-specific representation

  \(\begin{aligned} \mathbf{s}_{t}^{k} &=\mathbf{L} \mathbf{S} \mathbf{T} \mathbf{M}\left(x_{t}, \mathbf{s}_{t-1}^{k}, \theta_{s}\right) \\ \mathbf{h}_{t}^{k} &=\mathbf{L} \mathbf{S} \mathbf{T} \mathbf{M}\left(x_{t}, \mathbf{h}_{t-1}^{m}, \theta_{k}\right) \end{aligned}\).

3-2. Task-Specific Output Layer

parameters of network are trained to minimize CE loss!

\(L_{\text {Task }}=\sum_{k=1}^{K} \alpha_{k} L\left(\hat{y}^{(k)}, y^{(k)}\right)\).

• \(\alpha_k\) : weights for each tasks \(k\)

4. Incorporating Adversarial Training

No guarantee that sharable features cannot exist in private feature space

\(\rightarrow\) solution : ADVERSARIAL training into multi-task framework!

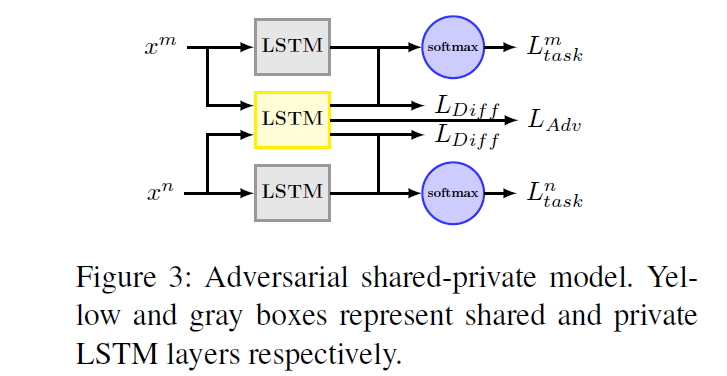
4-1. Adversarial Network

learn a generative distribution \(p_G(x)\) that matches real data distn \(P_{\text{data}}(x)\)

\(\begin{aligned} \phi &=\min _{G} \max _{D}\left(E_{x \sim P_{\text {data }}}[\log D(x)]\right. \left.+E_{z \sim p(z)}[\log (1-D(G(z)))]\right) \end{aligned}\).

4-2. Task Adversarial Loss for MTL

Shared recurrent neural layer is working adversarially towards a learnable multi-layer perceptrion,

preventing it from making an accurate prediction about the types of tasks.

(1) Task Discriminator

• estimate what kinds of tasks the encoded sentence comes from
• \(D\left(\mathbf{s}_{T}^{k}, \theta_{D}\right)=\operatorname{softmax}\left(\mathbf{b}+\mathbf{U s}_{T}^{k}\right)\).

(2) Adversarial Loss

• add extra task adversarial loss \(L_{A d v}\).

  ( to prevent task-specific feature from creeping into shared space )

• \(L_{A d v}=\min _{\theta_{s}}\left(\lambda \max _{\theta_{D}}\left(\sum_{k=1}^{K} \sum_{i=1}^{N_{k}} d_{i}^{k} \log \left[D\left(E\left(\mathrm{x}^{k}\right)\right)\right]\right)\right)\).

(3) Semi-supervised Learning Multi-task Learning

• \(L_{A d v}\) only requires input \(x\)
• not only utilize the data from related tasks, but can employ abundant unlabeled corpora

4-3. Orthogonality Constraints

• drawback : task-invariant features can appear both in shared & private space

• 1) penalize redundant latent representations

  2) encourages shared & private extractors to encode different aspects of the inputs!

• \(L_{\mathrm{diff}}=\sum_{k=1}^{K} \mid \mid \mathbf{S}^{k^{\top}} \mathbf{H}^{k} \mid \mid _{F}^{2}\).

  • \(\mid \mid \cdot \mid \mid _{F}^{2}\) : squared Frobenius norm
  • \(\mathbf{S}^{k}\) : whose rows are the output of shared extractor \(E_{s}\left(, ; \theta_{s}\right)\)
  • \(\mathbf{H}^{k}\): whose rows are the output of task-specific extractor \(E_{k}\left(; ; \theta_{k}\right)\)

4-4. Put it all together

\(L=L_{\text {Task }}+\lambda L_{\text {Adv }}+\gamma L_{\text {Diff }}\).