41.(paper) 13.Deriving Machine Attention from Human Rationales

13. Deriving Machine Attention from Human Rationales (2018)

목차

1. Abstract
2. Introduction
3. Related Work
4. Method
   1. Multi-task Learning
   2. Domain-invariant encoder
   3. Attention generation
   4. Pipeline

Abstract

Attention based models are widely used in NLP

In this paper, show that even in low-resource scenario, attention can be learned effectively

Start with discrete human annotated rationales and map them into continuous attention

1. Introduction

Propose an approach to “map human rationales to high-performing attention”

Machine-generated attention should mimic human rationales.

But, rationales on their own are NOT adequate substitutes for attention!

( \(\because\) instead of soft distn, human rationales only provide binary indication )

Propose R2A ( mapping from rationales \(\rightarrow\) attention )

• generalizable across tasks!

Consists of three components

• 1) attention-based model
• 2) domain-invariant representation
• 3) combine invariant representation & rationales

\(\rightarrow\) trained jointly to optimize the overall objective!

2. Related Work

• 1) Attention-based models

• 2) Rationale-based models

• 3) Transfer learning

  • transfer the knowledge by either

    (1) fine-tuning an encoder (trained on source tasks)

    (2) multi-task learning on all tasks (with shared encoder)

3. Method

(1) Problem formulation

• Source Task ( \(\left\{\mathcal{S}_{i}\right\}_{i=1}^{N}\) ) : sufficient label

• Target Task ( \(\mathcal{T}\) ) : scarce label

(2) Overview

• Goal : improve classification performance on target tasks by learning a mapping from R2A

• view R2A mapping as a meta model, that produces PRIOR over the attention distn

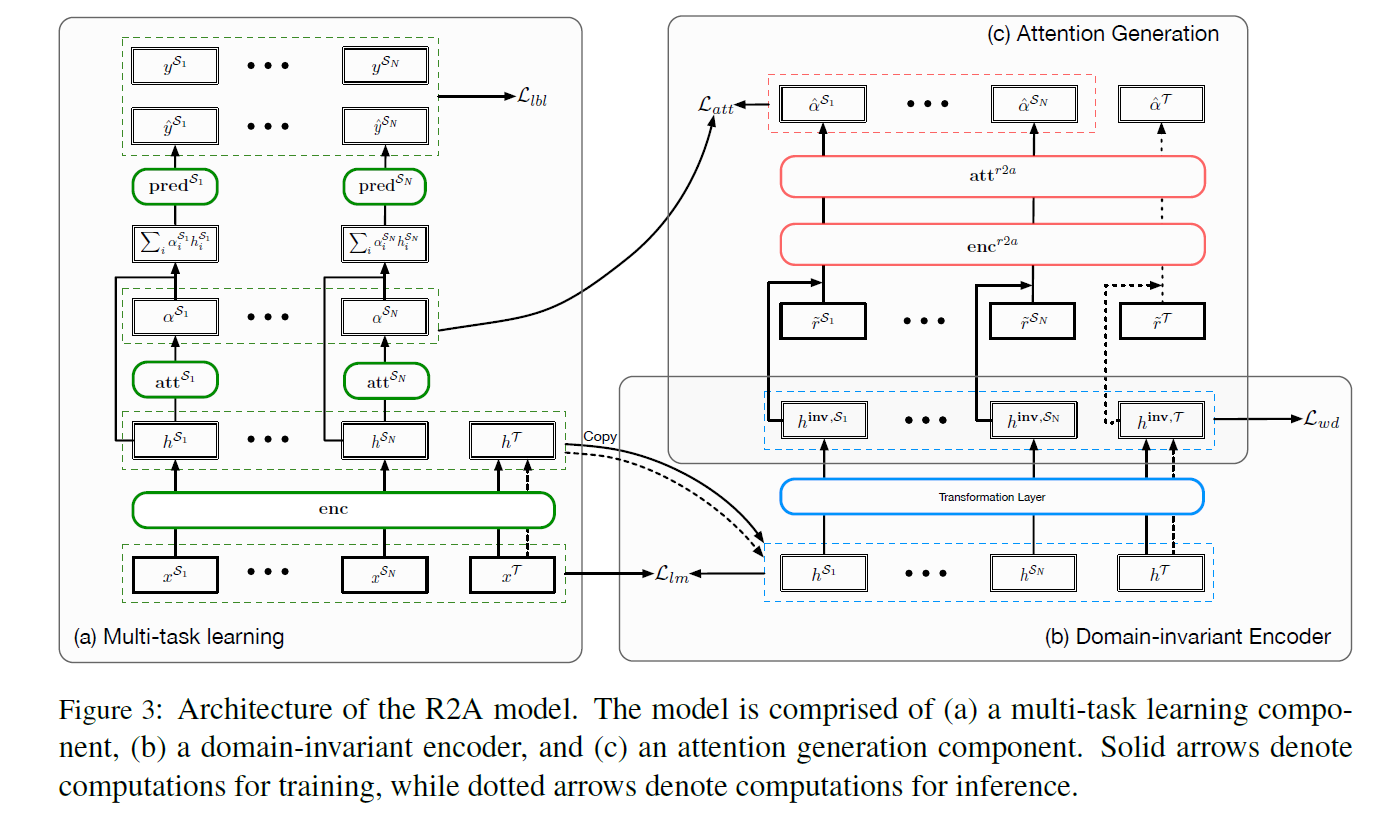
(3) Model Architecture

• Multi-task Learning
  • generated high-quality attention as an intermediate result
• Domain-invariant encoder
  • transform the contextualized representation (which is obtained from first module) into domain-invariant version
• Attention generation
  • predict the intermediate attention, obtained from the first module

3-1. Multi-task Learning

Goal : learn good attention for each source task

Notation : \(\left(x^{t}, y^{t}\right)\) = training instance, from any source task \(t \in\left\{\mathcal{S}_{1}, \ldots \mathcal{S}_{N}\right\}\).

Step

• step 1) encode the input sequence \(x^{t}\) into hidden states : \(h^{t}=\operatorname{enc}\left(x^{t}\right)\)
  • enc : bi-directional LSTM
  • \(h_{i}^{t}\) encodes the content and context information of the word \(x_{i}^{t}\)
• step 2) pass \(h^{t}\) on to a task-specific attention module & produce attention \(\alpha^{t}=\operatorname{att}^{t}\left(h^{t}\right)\)
  • \(\begin{aligned} \tilde{h}_{i}^{t} &=\tanh \left(W_{\text {att }}^{t} h_{i}^{t}+b_{\text {att }}^{t}\right) \\ \alpha_{i}^{t} &=\frac{\exp \left(\left\langle\tilde{h}_{i}^{t}, q_{\text {att }}^{t}\right\rangle\right)}{\sum_{j} \exp \left(\left\langle\tilde{h}_{j}^{t}, q_{\mathbf{a t t}}^{t}\right\rangle\right)} \end{aligned}\).
• step 3) predict label of \(x^t\)
  • using weighted sum of its contextualized representation
  • \(\hat{y}^{t}=\operatorname{pred}^{t}\left(\sum_{i} \alpha_{i}^{t} h_{i}^{t}\right)\).

Train this module to minimize the loss \(\mathcal{L}_{l b l}\) ( loss between prediction & annotated label )

3-2. Domain-invariant encoder

This module has 2 goals

• 1) learning a general encoder for both (1) source & (2) target corpora
• 2) learning domain-invariant representation

Notation

• \(x\) : input sequence
• \(h \triangleq[\vec{h} ; \overleftarrow{h}]\) : contextualized representation obtained from encoder

In order to support transfer, encoder should be GENERAL enough to represent both (1) source & (2) target corpora

Representation \(h\) is domain-specific.

Thus, apply transformation layer to obtain invariant representation!

• \(h_{i}^{\mathrm{inv}}=W_{\mathrm{inv}} h_{i}+b_{\mathrm{inv}}\).

Training objective :

• \(\begin{array}{rl} \mathcal{L}_{w d}=\sup _{ \mid \mid f \mid \mid _{L} \leq K} & \mathbb{E}_{h^{\text {inv }} \sim \mathbb{P}_{\mathcal{S}}}\left[f\left(\left[h_{1}^{\text {inv }} ; h_{L}^{\text {inv }}\right]\right)\right] -\mathbb{E}_{h^{\operatorname{inv}} \sim \mathbb{P}_{\mathcal{T}}}\left[f\left(\left[h_{1}^{\text {inv }} ; h_{L}^{\text {inv }}\right]\right)\right] \end{array}\).

3-3. Attention generation

Goal : generate high-quality attention for each task

\(r^t\) : task-specific rationales, corresponding to the input text \(x^t\)

Algorithm :

\(\begin{aligned} u^{t} &=\operatorname{enc}^{r 2 a}\left(\left[h^{\operatorname{inv}, t} ; \tilde{r}^{t}\right]\right) \\ \tilde{u}_{i}^{t} &=\tanh \left(W_{\mathbf{a t t}}^{r 2 a} u_{i}^{t}+b_{\mathbf{a t t}}^{r 2 a}\right), \\ \hat{\alpha}_{i}^{t} &=\frac{\exp \left(\left\langle\tilde{u}_{i}^{t}, q_{\mathbf{a t t}}^{r 2 a}\right\rangle\right)}{\sum_{j} \exp \left(\left\langle\tilde{u}_{j}^{t}, q_{\mathbf{a t t}}^{r 2 a}\right\rangle\right)} \end{aligned}\).

Minimize the distance between \(\hat{\alpha}^{t}\) and the \(\alpha^{t}\)

• ( \(\alpha^{t}\) = obtained from first multi-task learning module )

• \(\mathcal{L}_{a t t}=\sum_{\left(\alpha^{t}, \hat{\alpha}^{t}\right), t \in\left\{\mathcal{S}_{i}\right\}_{i=1}^{N}} \mathrm{~d}\left(\alpha^{t}, \hat{\alpha}^{t}\right)\).

  where \(\mathrm{d}(a, b) \triangleq \max (0,1-\cos (a, b)-0.1)\).

3-4. Pipeline

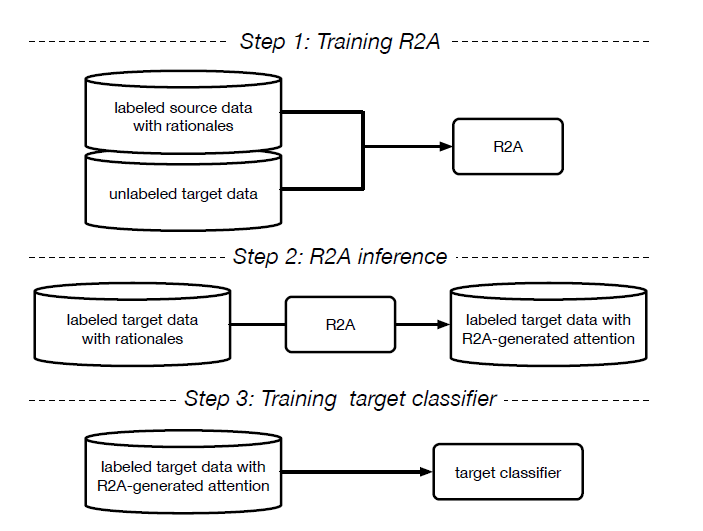
(1) Training R2A

• overall objective function : \(\mathcal{L}=\mathcal{L}_{l b l}+\lambda_{a t t} \mathcal{L}_{a t t}+\lambda_{l m} \mathcal{L}_{l m}+\lambda_{w d} \mathcal{L}_{w d}\).

(2) R2A inference

• after training R2A, generate attention for each labeld target

(3) Training target classifier

• when testing, neither provided with labels, nor rationales
• minimize prediction loss \(\mathcal{L}_{l b l}^{\mathcal{T}}\) & cosine-distance \(\mathcal{L}_{a t t}^{\mathcal{T}}\)
• objective of target classifier : \(\mathcal{L}=\mathcal{L}_{l b l}^{\mathcal{T}}+\lambda_{a t t}^{\mathcal{T}} \mathcal{L}_{a t t}^{\mathcal{T}}\).