[Paper Review] 02.GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium
Contents
- Abstract
- Introduction
- TTUR ( Two Time-Scale Update Rule ) for GANs
- Experiments
0. Abstract
GAN : excel at creating realistic images
BUT, “Convergence” has still not be proven!
\(\rightarrow\) propose a two time-scale update rule (TTUR)
TTUR : has an INDIVIDUAL LEARNING RATE for both discriminator & generator
1. Introduction
- FID score = LOWER, the BETTER
- Original GAN vs TTUR GAN
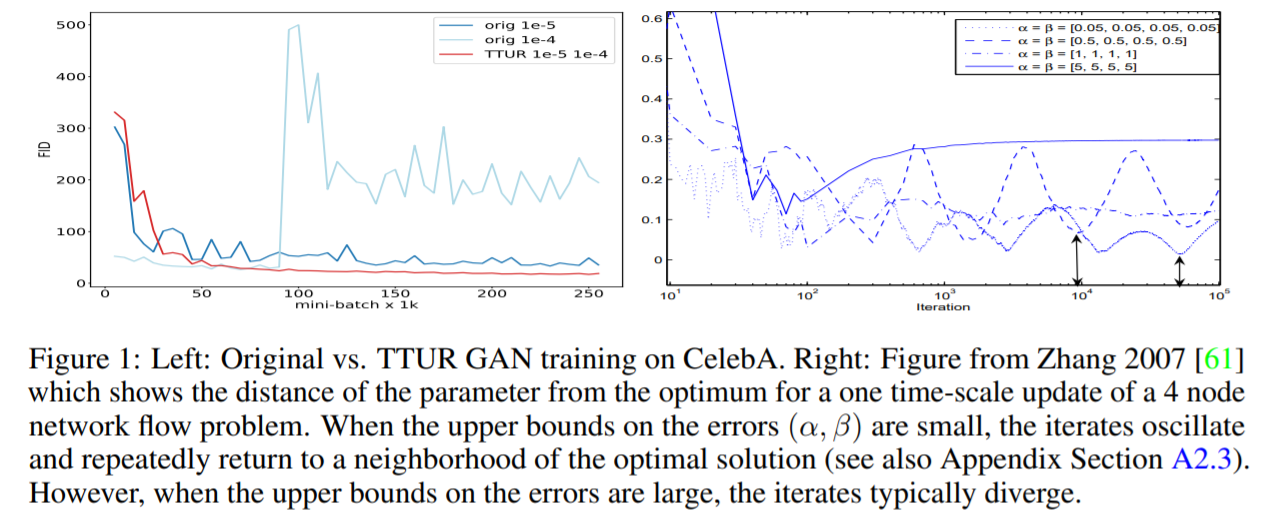
Contributions
-
1) two time-scale update rule for GANs
-
2) GANS trained with TTUR converge to stationary local Nash equilibrium
-
3) introduce FID (Frechet Inception Distance) to evaluate GANS
( more consistent than Inception score )
2. TTUR ( Two Time-Scale Update Rule ) for GANs
Notation
- \(D(. ; \boldsymbol{w})\) : discriminator
- \(G(. ; \boldsymbol{\theta})\) : generator
Gradients
Learning rate is based on..
- 1) a stochastic gradient \(\tilde{\boldsymbol{g}}(\boldsymbol{\theta}, \boldsymbol{w})\) of the discriminator’s loss function \(\mathcal{L}_{D}\)
- 2) a stochastic gradient \(\tilde{\boldsymbol{h}}(\boldsymbol{\theta}, \boldsymbol{w})\) of the generator’s loss function \(\mathcal{L}_{G}\)
( Gradients \(\tilde{\boldsymbol{g}}(\boldsymbol{\theta}, \boldsymbol{w})\) and \(\tilde{\boldsymbol{h}}(\boldsymbol{\theta}, \boldsymbol{w})\) are stochastic….. since they use mini-batches of \(m\) real world samples \(\boldsymbol{x}^{(i)}, 1 \leqslant i \leqslant m\) and \(m\) synthetic samples \(\boldsymbol{z}^{(i)}, 1 \leqslant i \leqslant m\) which are randomly chosen )
True gradients :
-
\(\boldsymbol{g}(\boldsymbol{\theta}, \boldsymbol{w})=\nabla_{w} \mathcal{L}_{D}\)…..\(\tilde{\boldsymbol{g}}(\boldsymbol{\theta}, \boldsymbol{w})=\boldsymbol{g}(\boldsymbol{\theta}, \boldsymbol{w})+\boldsymbol{M}^{(w)}\)
-
\(\boldsymbol{h}(\boldsymbol{\theta}, \boldsymbol{w})=\nabla_{\theta} \mathcal{L}_{G}\)…..\(\tilde{\boldsymbol{h}}(\boldsymbol{\theta}, \boldsymbol{w})=\boldsymbol{h}(\boldsymbol{\theta}, \boldsymbol{w})+\boldsymbol{M}^{(\theta)}\)
( with random variables \(\boldsymbol{M}^{(w)}\) and \(\boldsymbol{M}^{(\theta)}\) )
\(\rightarrow\) \(\tilde{\boldsymbol{g}}(\boldsymbol{\theta}, \boldsymbol{w})\) and \(\tilde{\boldsymbol{h}}(\boldsymbol{\theta}, \boldsymbol{w})\) are stochastic approximations to the true gradients!
Learning Rate \(b(n), a(n)\)
- discriminator’s LR : \(b(n)\)
- generator’s LR : \(a(n)\)
3. Experiments
Performance Measures
defining appropriate performance measures for generative models is HARD
-
ex) likelihood ( estimated by annealed importance sampling )
\(\rightarrow\) [drawback] heavily depends on noise assumptions
-
ex) Inception Score
- correlates with human judgements
- generated samples \(\rightarrow\) inception model trained on Image Net
- meaningful image = LOW entropy
\(\rightarrow\) [drawback] statistics of real world samples are NOT USED & compared to statistics of synthetic samples
Improve the Inception Score!
FID (Frechet Inception Distance) :
Fréchet distance \(d(., .)\) , between
- 1) the Gaussian with mean \((\boldsymbol{m}, \boldsymbol{C})\) obtained from \(p(\cdot)\)
- 2) the Gaussian with mean \(\left(\boldsymbol{m}_{w}, \boldsymbol{C}_{w}\right)\) obtained from \(p_{w}\) (.)
\(d^{2}\left((\boldsymbol{m}, \boldsymbol{C}),\left(\boldsymbol{m}_{w}, \boldsymbol{C}_{w}\right)\right)= \mid \mid \boldsymbol{m}-\boldsymbol{m}_{w} \mid \mid _{2}^{2}+\operatorname{Tr}\left(\boldsymbol{C}+\boldsymbol{C}_{w}-2\left(\boldsymbol{C} \boldsymbol{C}_{w}\right)^{1 / 2}\right)\).
