[Paper Review] 26.(i2i translation) Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

[Paper Review] 26. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Image-to-Image Translation
   2. Unpaired Image-to-Image Translation
   3. Cycle Consistency
   4. Neural Style Transfer
4. Formulation
   1. Adversarial Loss
   2. Cycle Consistency Loss
   3. Full Objective

0. Abstract

image-to-image translation

• learn the mapping between “input image” & “output image”
• ex) pix2pix

HOWEVER, for many tasks, paired training data will not be available

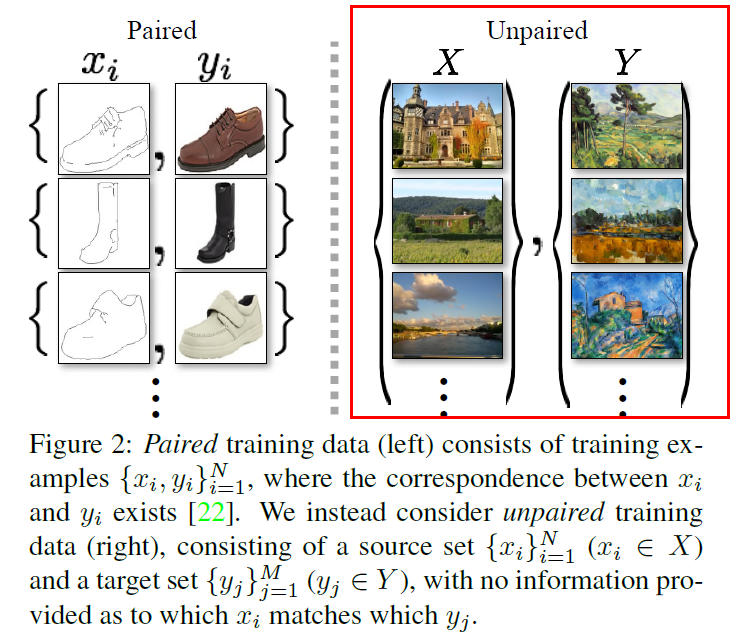
Goal :

• learn a mapping \(G\) : \(X \rightarrow Y\)

  such that, the distn of images from \(G(X)\) is indistinguishable from distn \(Y\)

• couple it with an inverse mapping \(F : Y \rightarrow X\)

• introduce a cycle consistency loss to enforce \(F(G(X)) \approx X\)

1. Introduction

seek an algorithm, that can learn to translate between domains,

WITHOUT paired input-output examples

although lack supervision in the form of paired examples..

still have supervision at the level of setes!

• given one “set” of images in domain \(X\)
• and a different “set” in domain \(Y\)

Train a mapping \(G : X \rightarrow Y\)

• such that \(\hat{y} = G(x)\) is indistinguishable from images \(y \in Y\)
• induce a output distn over \(\hat{y}\), that matches the empirical distn \(p_{data}(y)\)

Optimal \(G\)

• translates the domain \(X\) to a domain \(\hat{Y}\) distn identically to \(Y\)

BUT problem : mode collapse

Solution :

• exploit the property that translation should be “cycle consistent”

  ( = should arrive back! )

• [mathematically]

  • if we have translator \(G : X \rightarrow Y\)
  • and another translator \(F : Y \rightarrow X\)
  • \(G\) and \(F\) should be inverses of each other

• add a cycle consistency loss that encourages..

  • \(F(G(x)) \approx x\) and \(G(F(y)) \approx y\)

2. Related Work

1) Image-to-Image Translation

• our approach builds upon “pix2pix”

  ( use conditional adversarial network )

2) Unpaired Image-to-Image Translation

• relate two data domains : \(X\) & \(Y\)

• does not rely on any task-specific, predefined similarity function between input & output

  \(\rightarrow\) general-purpose solution

3) Cycle Consistency

• “back translation and reconciliation”

4) Neural Style Transfer

• one way to perform image-to-image translation
• combine..
  • 1) content of one image
  • 2) with the style of another image
• BUT primary focus of CycleGAN :
  • mapping between image collections, rather than between two specific images

3. Formulation

Goal : learn mapping function between two domains \(X\) & \(Y\)

• training samples :
  • \(\left\{x_{i}\right\}_{i=1}^{N}\) where \(x_{i} \in X\)
  • \(\left\{y_{j}\right\}_{j=1}^{M}\) where \(y_{j} \in Y\)
• two mappings :
  • \(G: X \rightarrow Y\).
  • \(F: Y \rightarrow X\).
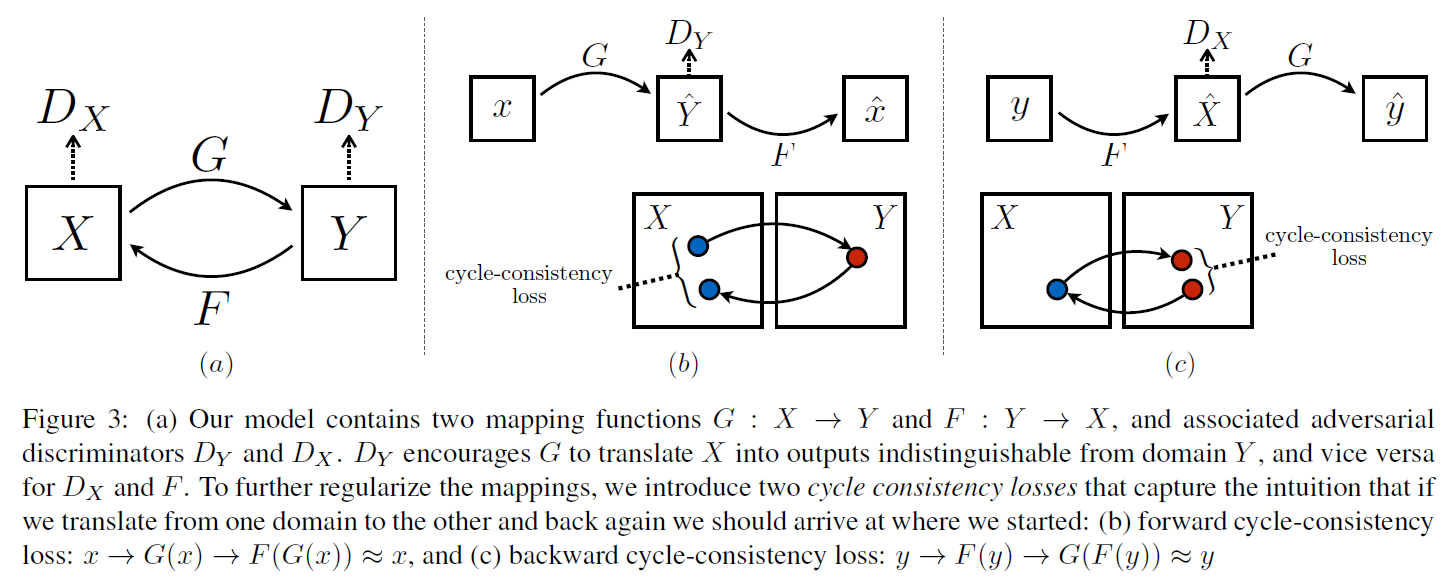
• introduce 2 adversarial discriminators \(D_X\) and \(D_Y\)
  • \(D_{X}\) : distinguish between images \(\{x\}\) and translated images \(\{F(y)\}\)
  • \(D_{Y}\) : discriminate between \(\{y\}\) and \(\{G(x)\}\)
• two terms in objective
  • 1) adversarial losses
  • 2) cycle consistency losses

1) Adversarial Loss

a) for mapping \(G\)…

• \[\mathcal{L}_{\mathrm{GAN}}\left(G, D_{Y}, X, Y\right) =\mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\log D_{Y}(y)\right] +\mathbb{E}_{x \sim p_{\text {data }}(x)}\left[\log \left(1-D_{Y}(G(x))\right]\right.\]

b) for mapping \(F\)…

• introduce similar loss for mapping \(F\)

2) Cycle Consistency Loss

Adversarial Loss ALONE cannot guarantee, that the learned function

can map an individual input \(x_i\) to desired output \(y_i\)

Learned mapping should be “cycle-consistent”

• 1) Forward Cycle Consistency
  • \(x \rightarrow G(x) \rightarrow F(G(x)) \approx x\).
• 2) Backward Cycle Consistency
  • \(y \rightarrow F(y) \rightarrow G(F(y)) \approx y\).

Cycle Consistency Loss :

• \(\mathcal{L}_{\text {cyc }}(G, F) =\mathbb{E}_{x \sim p_{\text {data }}(x)}\left[ \mid \mid F(G(x))-x \mid \mid _{1}\right] +\mathbb{E}_{y \sim p_{\text {data }}(y)}\left[ \mid \mid G(F(y))-y \mid \mid _{1}\right]\).

3) Full Objective

Final Objective :

• \(\begin{aligned} \mathcal{L}\left(G, F, D_{X}, D_{Y}\right) &=\mathcal{L}_{\mathrm{GAN}}\left(G, D_{Y}, X, Y\right) \\ &+\mathcal{L}_{\mathrm{GAN}}\left(F, D_{X}, Y, X\right) \\ &+\lambda \mathcal{L}_{\mathrm{cyc}}(G, F) \end{aligned}\).

Thus, aim to solve..

• \(G^{*}, F^{*}=\arg \min _{G, F} \max _{D_{x}, D_{Y}} \mathcal{L}\left(G, F, D_{X}, D_{Y}\right)\).

Can be viewed as training two “autoencoders” ! Learn

• one autoencoder \(F \circ G: X \rightarrow\) \(X\)
• jointly with another \(G \circ F: Y \rightarrow Y\)