[Paper Review] 05.Reliable Fidelity and Diversity Metrics for Generative Models
Contents
- Abstract
- Introduction
- Background
- Evaluation pipeline
- Fidelity and Diversity
- Density and Coverage
- Problems with improved precision & recall
- Density & Coverage
0. Abstract
problem of FID score
- does not differentiate fidelity and diversity aspects of generated images
- recent papers have introduced variants…but still not relabile
\(\rightarrow\) propose DENSITY and COVERAGE metrics!
1. Introduction
necessary conditions for useful evaluation metrics :
- (1) ability to detect identical real and fake distributions
- (2) robustness to outlier samples
- (3) responsiveness to mode dropping
- (4) the ease of hyperparameter selection in the evaluation algorithms
propose density and coverage metrics
- not only make the fidelity-diversity metrics empirically reliable
- but also theoretically analysable
study the embedding algorithms for evaluating image generation algorithms
-
( embedding pipeline has been relatively less studied )
-
( mostly rely on the features from an ImageNet pretrained model )
$\rightarrow$ inevitably include the dataset bias
-
SOLUTION : To exclude the dataset bias, use randomly initialised CNN feature extractors
-
+ random embeddings : more sensible evaluation results, especially when the target data distribution is significantly different from ImageNet statistics
2. Background
- real distribution : \(P(X)\)
- generative model : \(Q(Y)\)
\(\rightarrow\) assume that we can sample \(\left\{X_{i}\right\}\) and \(\left\{Y_{j}\right\}\)
Statistical testing methods ( or distributional distance measures )
- ex) KL-divergence, Expected Likelihood
when \(P(X)\) are complex & high-dim \(\rightarrow\) difficult to apply such measures naively
(1) Evaluation pipeline
step 1) embed real & fake sample \(\left\{X_{i}\right\}\) and \(\left\{Y_{j}\right\}\) into Euclidean space \(\mathbb{R}^{D}\)
- using non-linear mapping \(f\) ( ex. CNN feature extractor )
step 2) construct real & fake distn over \(\mathbb{R}^{D}\) with the embedded samples \(\left\{f\left(X_{i}\right)\right\}\) , \(\left\{f\left(Y_{j}\right)\right\}\)
step 3) quantify discrepancy between the two distributions
[step 1] embedding
difficult to define a sensible metric
-
ex) \(\ell_{2}\) distance over the image pixels \(\mid \mid X_{i}-Y_{j} \mid \mid _{2}\)
( often misleading )
-
ex) \(\ell_{2}\) distance in the feature space \(\mid \mid f\left(X_{i}\right)-f\left(Y_{j}\right) \mid \mid _{2}\)
for embedding… adopt ImageNet pre-trained CNNs
-
when using data distn DISTINCT from Image Net distribution…
suggest using randomly-initialised CNN feature extractors
[step 2] Building & Comparing distributions
- Given embedded samples \(\left\{X_{i}\right\}\) and \(\left\{Y_{j}\right\}\)
- (non-)parametric statistical approximation
- Parzen window estimates
- approximate the likelihoods of the fake samples \(\left\{Y_{j}\right\}\) by estimating the density \(P(X)\) with Gaussian kernels around the real samples \(\left\{X_{i}\right\} .\)
- Inception Score
- estimate the multinomial distribution \(P\left(T \mid Y_{j}\right)\) over 1000 ImageNet classes
- compares it against the estimated marginalized distn \(P(T)\), using KL-divergence
- FID
- distance between 2 Gaussians
- Parzen window estimates
(2) Fidelity and Diversity
Trade-off between Fidelity and Diversity
Fidelity
- how realistic each input is
Diversity
- how well fake samples capture the variations in real samples
2. Density and Coverage
Introduce variants of two-value metrics, Density & Coverage
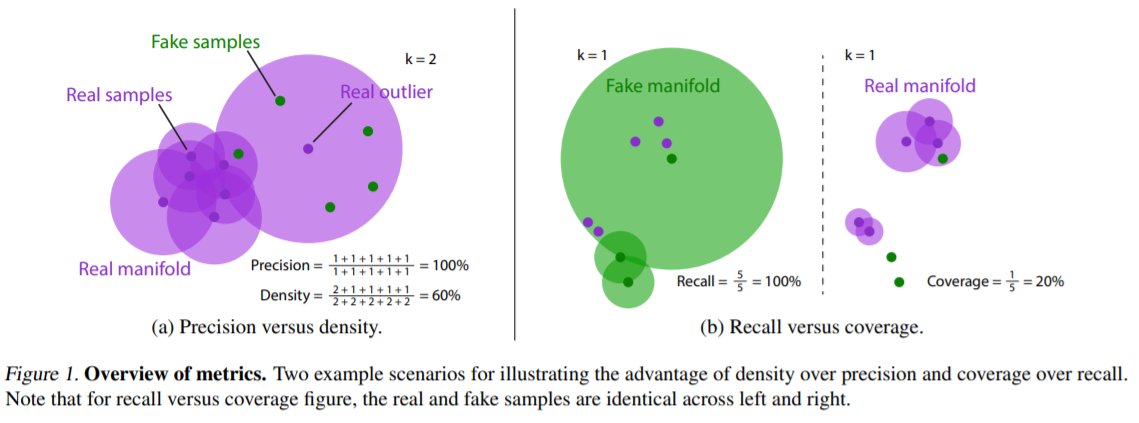
(1) Problems with improved precision & recall
( 참고 : https://seunghan96.github.io/gan/(gan4)Improved-Precision-and-Recall-Metric-for-Assessing-Generative-Models/ )
-
use KNN
- vulnerability to outliers & computational inefficiency
- generally overestimate the true manifold around outliers
(2) Density & Coverage
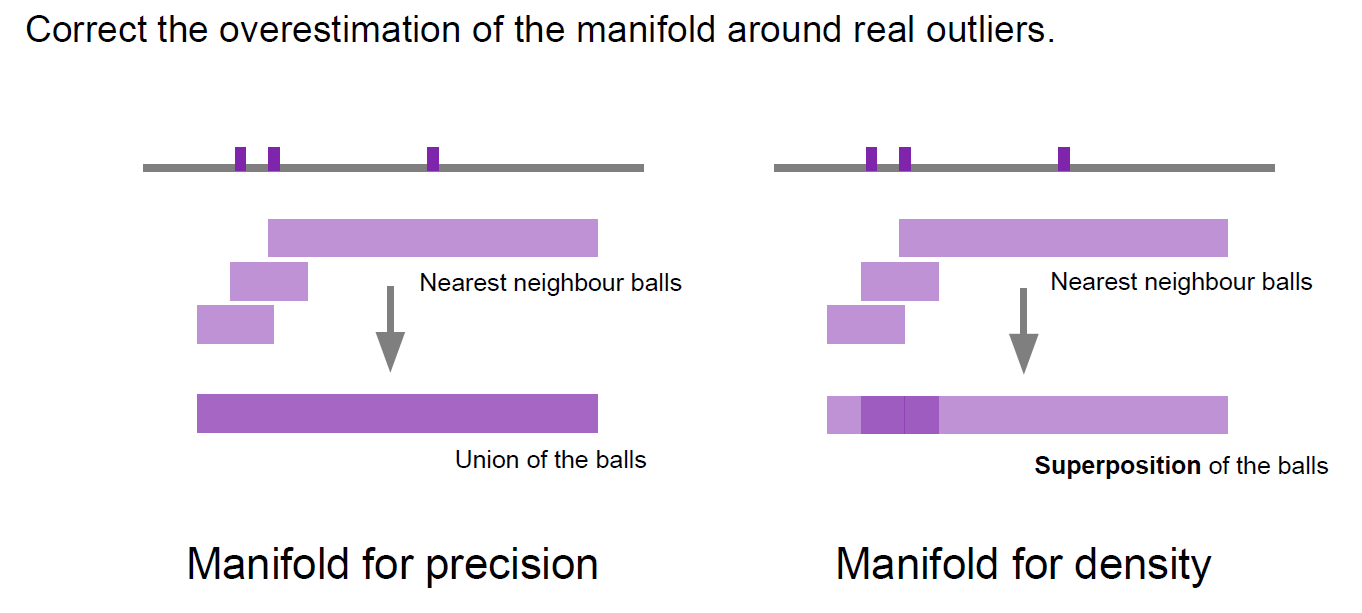
- 출처 : (연세대학교 어영정 교수님) 생성적적대적신경망 강의 자료
