Multi Label Classification
[ Metric ]
Classification Model을 만든 이후, 우리는 어떤 모델이 가장 최적인지 선택할 필요가 있다. 그 선택의 기준이 될 수 있는 지표에는 여러가지가 있다. 그 중에서도, Multi Label Classificaiton 문제에서 흔히 사용되는 지표로 F1 score(F1, Micro-F1, Macro-F1)에 대해 알아볼 것이다. 이를 알아보기 전에, 일반적인 classification 문제에서 사용되는 기본적인 지표인 Precision, Recall, Accuracy등이 있는데 이를 먼저 간단히 짚고 넘어가자.
[ Precision, Recall, Accuracy ]
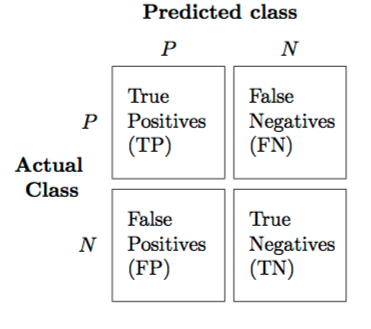
- Precision : “Positive이라고 예측한 것 중, 실제로 Positive인 것의 비율” ( TP / (TP+FP) )
- Recall : “실제로 Positive인 것 중, Positive라고 예측한 것의 비율” ( TP / (TP+FN) )
- Accuracy : “옳게 예측한 것(=정답)의 비율” ( (TP+TN) / (TP+FP+TN+FN) )
위 지표를 보면, Precision과 Recall은 서로 trade-off관계임을 알 수 있다. 0~1사이 반환되는 확률 값에서, 특정값 x를 넘으면 1로, 아니면 0으로 분류하는 문제가 있다고 하자. 이 x를 높일 수록(1이라고 예측하는 기준 컷을 높일 수록), Positive이라고 예측하는 것(P)의 수가 줄어들어 (실제로 옳은 개수는 불변함으로) Recall값은 줄어들게 되고, Precision값은 늘어날 수 밖에 없다. 그래서 처한 문제의 상황에 따라, 어떤 지표가 적절한지 선택할 필요가 있다. 하지만 정확히 어떤 지표가 정확한 지표이다!라고 판단하기에 어려울 수 있기 때문에, 이 두 지표를 둘 다 반영한 새로운 지표가 있는데, 그것이 F1 score이다.
[ F1-score ]
F1-score는 Precision과 Recall을 조합하여 만든 새로운 지표다. 이 둘을 단순 산술 평균(arithmetic mean)한게 아니라, 조화 평균(harmonic mean)한 값이다. 그 식은 다음과 같다.
F1-score = 2 × (precision × recall)/(precision + recall)
우선 Binary Classifier를 예시로 들어보자. F1-score는 항상 Precision과 Recall사이에 놓이게 될 것이다. 하지만, 이 둘 중 어느거에 더 weight가 있는지는, 그 크기에 따라 다른다. F1-score는, 둘 중 더 낮은 값에 영향을 더 많이 받는다. Classifier A의 Precision과 Recall이 둘다 80%로, 산술 평균으로 80%이다. 산술 평균으로 똑같이 80%지만, Recall이 60%고 Precision이 100%인 Classifier B가 있다고 해보자. Classifier A의 F1-score는 당연히 80%일 것이고, Classifier B의 F1-score는 75%로, 단순 평균인 80%보다 낮다. 더 작은 값인 Recall(60%)에 의해 영향을 더 많이 받는 것이다.
이제 이 문제를, Binary가 아닌 Multi Label(Class) Classification 문제로 확장시켜서 생각해보자.
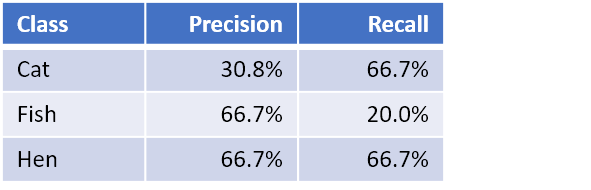
Multi Label Classification 문제이기 때문에, 여러 개의 Recall & Precision값이 생기게 될 것이다. 이럴 경우에는, Label 별로 F1-score가 생기게 될 것이다. 위의 예시로 보면, Cat의 F1-score는 42.1% ( = 2 × (30.8% × 66.7%) / (30.8% + 66.7%) )가 될 것이다. Fish, Hen에 대해서도 F1-score를 구하면 각각 30.8%, 66.7%가 된다. 이렇게 생기게 되는 여러 개의 F1-score들을 어떻게 종합하여 하나의 score로 나타낼 것인가에 있어서도 두 가지 방법이 있다.
그 두 지표는 ‘micro F1-score’와 ‘macro F1-score’이다.
1. Macro F1-score
여러 F1-score들을 단순 평균한 방법이다. 위 식에서는, 각각의 Label에 동일한 가중치를 두어서 평균내었다.
Macro-F1 = (42.1% + 30.8% + 66.7%) / 3 = 46.5%
하지만, Label별로 가중치를 반영하기 위해, 각 Label에 속한 data의 수 만큼 가중치를 주는 방법도 있다(Weighted Average F1-score). 위 예시를 통해 구하면, 다음과 같다.
Weighted Average F1-score = (6 × 42.1% + 10 × 30.8% + 9 × 66.7%) / 25 = 46.4%
2. Micro F1-score
Micro (Averaged) F1-score를 구하기 위해, 우선 Micro Precision과 Micro Recall에 대해 알아야 한다.
1) Micro Precision
여기서 말하는 ‘Micro’(혹은 Micro Average)를 구하는 방법은 간단하다. 기존의 binary문제에서 풀던 TP(True-Positive)는, “실제로 Positive인 것 중 Positive라고 예측한 것”을 의미하였다. 하지만 Micro Average를 구할 때에 있어서는, TP는 “옳게 예측한 것(=정답)”을 의미한다.(위 예시에서는 4+2+6=12). 또한, 기존의 문제에서 정의하던 FP (“Positive라고 예측했지만, 실제로 Negative인 것”)은, “잘못 예측한 것(=오답)”을 의미한다. 즉, Micro에서 말하는 TP와 FP를 합하면 전체 데이터 수가 된다. 그렇기 때문에, 위 예시에서 구한 Micro Precision은 12/(12+13)= 48.0%이다.
2) Micro Recall
Micro Recall의 공식은 TP/(TP+FN)이다. TP는 위에서(Micro Precision)에서 구한 대로 구하면 된다(위 예시에서 12). FN의 정의를 살펴보면, “Negative라고 예측한 것 중 실제로는 Positive인 것”이다. Micro 상황에서 정의하자면, 이는 결국 “오답”과 동일하다. 그렇기 때문에, 위 예시에서 Micro Recall은 12/(12+13)= 48.0%. 즉, Micro 문제에서는 Recall이나 Precision은 같게 된다. 이 두 지표는 또한, 옳게 예측한 비율을 나타내는 Accuracy와도 같게 된다.
Micro F1 = Micro Precision = Micro Recall = Accuarcy
[ Summary ]
절대적으로 옳은 지표는 없다. 기본적인 지표로 Precision, Recall, Accuracy등이 있고, 이를 보완하기 위해 (Precision과 Recall을 조합한) F1-score가 있다. 하지만 F1-score 또한 절대적으로 맞는 지표라고 할 수 없다. Multi Label Classification 문제에서 많이 사용되는 지표이긴 하지만, 이 또한 절대적인 모델의 판단 기준이 될 수 없다. 그렇기 때문에 상황에 따라 최선의 지표를 선택하여 사용하는 것이 중요하다.
