(paper) DeepWalk, Online Learning of Social Representations

Network내에서 vertices(node)들의 latent representation(잠재적 표현)을 학습하는 방법
( walk? Vertices들 끼리 연결된 edge를 계속 따라가는 것이라고 보면 된다. NLP에서 sentence와 동일한 역할 )
60%의 training data로도 다른 baseline method들보다 더 뛰어난 성능을 보이는 것으로 기록되었다
(확장 가능성) Network Classification, Anamaly Detection에서도 사용될 수 있다

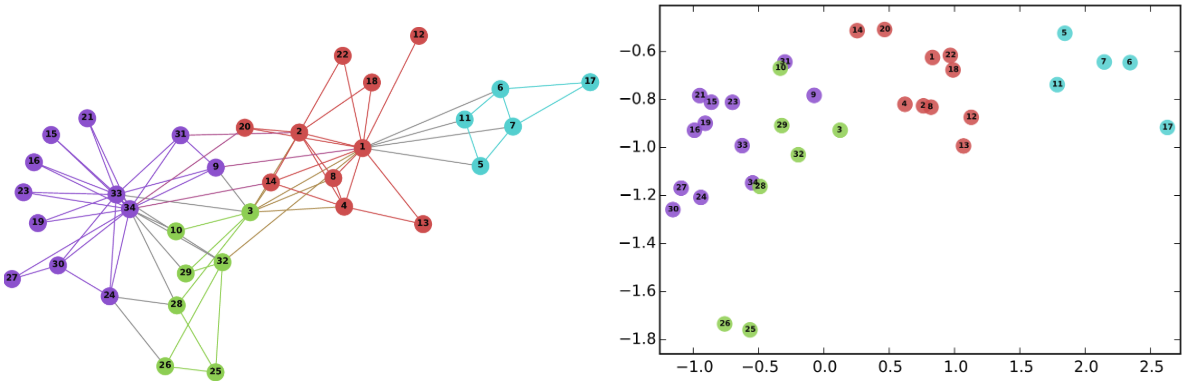
[ Example 1 : 34차원의 Karate Graph를 2차원 상의 공간에 표현 ]
왼쪽의 그래프는 34차원의 Karate graph이다. 이 34차원의 공간을, 2차원 상의 공간으로 embedding하여 표현하였을 때(오른쪽 그림), 그 형태가 잘 유지됨을 확인할 수 있다
( 형태 유지 = 같은 label들이 뭉쳐 있다 = 2차원에서의 거리가 실제 차원에서의 거리를 잘 반영한 표현이다 )
Karate Graph

[ 1. Introduction ]

KEY : 고차원의 sparse한 data를 어떻게 처리할 것인가? 어떻게 축소하여 표현할 것인가?
목표 : “develop an algorithm that learns SOCIAL REPRESENTATIONS of graph’s vertices”

INPUT : graph ( 고차원 상의 network )

OUTPUT : latent representation
위의 input을 어떻게 잘 표현할 것인가?
( 잘 표현한다 = “실제 데이터에서 서로 다른 두 vertice가 유사하다면, latent representation에서도 두 vertice가 유사하게 되도록 표현된다” )

EVALUATION

multi-label Network Classification 문제에 적용해봄으로써 성능을 평가할 수 있다!
위의 Example 1을 보면, 기존의 data에서 같은 class에 속한 데이터들이 2차원의 공간에 표현되었을 때도 같은 class끼리 인접하게 위치함으로써, 그 형태를 잘 유지한 것을 확인할 수 있다.

DeepWalk’s Contribution

short random walk를 통해서도 기존 데이터의 구조를 잘 잡아낼 수 있다
sparse한 data를 잘 represent할 수 있다 ( 기존의 모델들보다 더 적은 데이터로도 뛰어난 성능을 보임을 입증 )
병렬처리가 가능하다 ( graph의 여러 vertex에서 동시에 random walk를 시행할 수 있다 )

[ 2. Problem Definition ]

“Classify members of social network into one or more categories”

G = (V,E)

V : vertex (node, 네트워크 상의 member)
E : edge (vertex들 간의 연결)

UNSUPERVISED Learning
Supervised learning의 classification 문제와는 다르게, 그래프(네트워크)의 구조를 파악하기 위해 Label을 사용하지 않는다.
( captures the graph structure INDEPENDENT of the label’s distribution )

GOAL
“Network상의 Member들 간의 관계를, 저차원 상의 공간으로 분산하여 표현한다!”

다음의 특징을 가지고 social representation을 학습!
1) Adaptability : 새로운 data가 추가 되어도, 전체를 다시 학습할 필요 없음! ( Online Learning ) 2) Community aware : latent dimension 차원에서 정의되는 distance는, 실제 network 상의 social similarity를 평가할 수 있는 metric이어야 함! 3) Low Dimension : 저차원으로 표현하여 더 빠르고 일반화하기 좋은 모델로 만들어야! 4) Continuous : smooth decision boundary

3.1 Random Walk

$W_{v_{i}}$ : random walk rooted at vertex $v_{i}$
하나의 Vertex에서 시작하여, 연결된 edge를 따라 가는 것이라고 보면 된다.
Random Walk는 content recommendation, community detection 등의 문제에서 similarity measure로 사용된다

random walk를 사용해서 좋은 점?
1) Local Exploartion is easy to Parallelize! ( network graph 상의 여러 space에서 동시에 탐색 가능 ) 2) graph 상의 일부분의 변화로, 전체를 recompute할 필요가 없음! ( online learning 가능 )

3.2 Connection : Power Laws

network graph가 power-law를 따른다면, random walk에서 등장하는 vertices들의 frequency도 power-law를 따른다!
NLP에서 사용되는 기법을, 이 분석에서도 사용할 수 있다. 아래 그림의 왼쪽은 random walk에서 vertex가 등장하는 횟수를 나타낸 그래프이고, 오른쪽 그림은 Wikipedia의 text 데이터로 단어의 등장 횟수를 나타낸 그래프이다. 이 둘이 비슷한 모습을 보임으로써, network 구조에서도 power law distribution을 가져와서 사용하는 것을 정당화 할 수 있다.

3.3 Language Modeling

LM의 목표 : estimate the likelihood of a specific sequence of words apperaing in a corpus!
( Input으로 W(sequence of words)가 주어졌을 때, $Pr(w_{n}|(w_{0},w_{1},...,w_{n-1}))$ 를 maximize하기 )

여기서, Walk = Short Sentence로 생각하면 된다. word 대신 위에서 배운 vertex로 생각해보면,

$Pr(v_{i}|(v_{1},v_{2},...,v_{i-1}))$ 로 표현 가능하고,

Latent Representation으로 표현하는 mapping function( $\Phi : v\in V \mapsto \mathbb{R}^{|V|\times d}$ )에 적용하면

$Pr(v_{i}|(\Phi (v_{1}),\Phi (v_{2}),...,\Phi (v_{i-1})))$ 를 maximize하는 문제로 볼 수 있다.

OBJECTIVE FUNCTION 하지만 walk length가 길어질 수록, 위의 조건부 확률 식을 구하기 어려워진다. 이를 해결하기 위해, context로 하나의 target word를 예측하는 대신, 하나의 word로 context를 예측하는 구조로 변형한다. 또한, context를 특정 단어의 이전(left)로 정의하지 않고, 특정 단어의 양쪽(left & right)에 등장하는 단어들로 정의한다.
그렇기 때문에 위에서 나온 식을 푸는 것 대신, 아래 식을 minimize함으로써 optimization을 시행한다.

minimize $-logPr({v_{i-w},...,v_{i+w}} / v_{i} | \Phi (v_{i-1}))$
위의 식을 통해 optimization 문제를 풀 경우, 실제 공간에서 인접한 vertices들은 latent 공간에 represent 되어서도 인접하게 될 것이다!

[ 4. METHOD ]

network에서 random walk와 vertices는 각각 NLP에서의 corpus, vocab로 볼 수 있다

(NLP) corpus = (Network) short truncated random walks
(NLP) vocabulary = (Network) graph vertices

4.1 DeepWalk Algorithm

1) graph G를 input으로 받아서, random walk $W_{V_{i}}$ 의 root로써 random vertex $v_{i}$ 를 random sample한다
2) Outer Loop : 하나의 vertex에서 ‘몇 번의 random walk’( $\gamma$ )를 할 지!
3) Inner Loop : graph내의 모든 vertice에서 iterate
( 모든 vertex $v_{i}$ 에서, random walk $|W_{v_{i}}|=t$ 를 생성하고, SkipGram을 사용하여 이것을 update

4.2 Skip Gram & Hierarchical Softmax

1) Skip Gram
특정 단어와, 그 단어의 window 내에 있는 단어들과 함께 등장(co-occurence)하는 확률을 maximize하는 LM
독립성의 가정에의해, LM의 objective function을다음과 같이 나타낼 수 있다
$Pr(\left \{v_{i-w},...v_{i+w}\right \}/v_{i} | \Phi (v_{i})) = \prod_{j=i-w}^{i+w}Pr(v_{j}|\Phi (v_{i}))$

Skip Gram은 다음과 같은 방법을 통해 update를 한다.

위에서 보이는 바와 같이, Skip Gram algorithm은 (window w 내에 등장하는) 모든 random walk를 iterate한다. 하지만, 이럴 경우 computational cost가 너무 커서, 이 방법 대신 Hierarchical Softmax를 사용하여 확률 분포를 근사한다!

2) Hierarchical Softmax
위의 SkipGram Algorithm의 line3 ( $Pr(v_{j}|\Phi (v_{i}))$ )를 전부 계산 하는 것은 computational cost가 너무 크다. 그러기 때문에, 우리는 이 식을 factorize하여 Hierarchical Softmax를 통해 구한다. (구체적인 내용은 다음 포스트 참고)

각각의 vertex는 binary tree의 leave가 되고
prediction problem은 hierarchy에서 specific path의 확률을 극대화 하는 문제가 된다.
이를 식으로 나타내면 다음과 같다.
$Pr(u_{k}|\Phi (v_{j})) = \prod_{l=1}^{\left \lceil log|V| \right \rceil} Pr(b_{l}|\Phi (v_{i}))$

여기서 b(0),b(1),….b(log(V))는 root에서 vertex u(k)까지 가는 path이다.
( b(0)는 root, b(log(V))는 u(k) )

위 식에서 $Pr(b_{l}|\Phi (v_j))$ 는, hierarchical softmax의 binary tree에 의해 다음과 같이 표시할 수 있다.

$Pr(b_{l}|\Phi (v_j))=1/(1+e^{-\Phi(v_j)\cdot \Psi (b_l)}))$

여기서 $\Psi (b_l) \in \mathbb{R}^d$ 는 b(l) node의 parent node의 vector 표현이다.

이 방법을 통해, 연산량을 O(V)에서 O(log(V))로 획기적으로 줄일 수 있다!
( ex. 1024개의 단어가 있으면, 기존에는 연산량이 O(1024)였다면, hierarchical softmax의 binary tree 방식 덕분에 연산량이 O(10) ( 10 = ( $log_21024$ )으로 줄어들 수 있다.

Twitter Facebook LinkedIn

(paper) DeepWalk, Online Learning of Social Representations

Seunghan Lee

[ 1. Introduction ]