Node2vec : Scalable Feature Learning for Networks
1. Introduction
- semi-supervised algorithm for scalable feature learning in networks
- “learning continuous feature representations for nodes in network” ( into low dimension )
( classical approach : PCA, Multi-Dimensional Scaling ) - use 2nd order random walk approach to generate network neighborhoods ( contribution : defning a flexible notion of a node’s network neighborhood )
- use feature representations not only of nodes, but also “edges”
[ KEY CONTRIBUTION ]
- efficient scalable algorithm for feature learning in networks (using SGD)
- provides flexibilty in discovering representations
- extend node2vec from ‘nodes’ -> ‘edges’
- evaluate node2vec for (1) multi-label classification & (2) link prediction
- (1) multi-label classification : which class does each node belongs to
- (2) link prediction : predict whether there is a connection between two nodes
2. Feature learning Framework
- applicable to any (un)directed & (un)weighted network
- extend Skip-Gram architecture to networks
** skip-gram : https://github.com/seunghan96/datascience/blob/master/%5B%EC%97%B0%EA%B5%AC%EC%8B%A4%EC%9D%B8%ED%84%B4%5DComputing_Science_and_Engineering/1%EC%A3%BC%EC%B0%A8/DeepWalk_Online_Learning_of_Social_Representations.md - propose a randomized procedure that samples many different neighbors of a source node!
- network :
mapping function (from nodes -> feature representations) :
( d : number of dimension of feature representation )
(: matrix size of
)
network neighborhood of node u ( generated by neighborhood sampling strategy S ):
[ Objective Function ]
- maximize log-probability of observing a network neighborhood (
) for a node u, conditioned on its feature representation( = f(u) )
[ Two Assumptions ]
1) Conditional Independence
- factorize the likelihood, by assuming independence among likelihood of obesrving a neighborhood nodes
2) Symmetry in feature space
- source node & neighborhood node -> have symmetric effect over each other in feature space
- conditional likelihood of source-neighborhood node pair ( as a softmax ) :
with these two assumption, the objective function can be simplified into
( in the above, is too expensive to compute! use negative sampling )
** negative sampling : https://github.com/seunghan96/datascience/blob/master/%5B%EC%97%B0%EA%B5%AC%EC%8B%A4%EC%9D%B8%ED%84%B4%5DComputing_Science_and_Engineering/4%EC%A3%BC%EC%B0%A8/Negative_Sampling.md
3-1. Classic search strategies
- sample neighbors of a source node as a form of local search
[ two kind of similarities ]
1) homophily
- highly interconnected -> should be embedded closely
- macro view
- infer communities based on distances
( ex. u & s1 : community A, s8 & s9 : community B )
2) structural equivalence - similar structural roles -> embedded together
- micro view( example with the image above : u & s6 )
- does not emphasize connectivity!
( ex. u & s6 : act as hubs of communities )
[ two search algorithms ]
- two sampling strategies for generating neighborhood sets N(s) of k nodes ( BFS & DFS )

(https://i.stack.imgur.com/vm0sn.png)
a. Breadth-first Sampling(BFS)
- neighborhood : only immediate neighbors of the source node
- micro-view
- for ‘structural equivalence’
b. Depth-first Sampling(DFS)
- neighborhood : nodes sequentially sampled at increasing distance from the source node
- macro-view
- for ‘homophily’
** BFS & DFS implementation : (https://github.com/seunghan96/datascience/tree/master/Data_Structure/2.Algorithm/Graph_Algorithm)
3-2. node2vec
- interporlate between BFS & DFS
- by developing a flexible biased random walk procedure ( that can explore neighborhoods both in BFS & DFS fashion )
(1) Random Walks

(2) Search bias 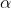
- simple way to bias randm walk : based on edge weights -> hard to find different types of network structure
- ( REMEMBER! homophily & structure equivalence are not in trade-off ! So, how to achieve both? )
[ Second order random walk with 2 parameters, p & q ]
Example
- passed the edge (t,v) just before! ( previous state : node t & current state : node v )
- to decide next step, evaluate transition probability
-
set the unnormalized transition probability to
 </a>
</a>
is the shortest path distance between node t & x -> minimum 0, maximum 2)
 </a>
https://www.mdpi.com/algorithms/algorithms-12-00012/article_deploy/html/images/algorithms-12-00012-g004.png
</a>
https://www.mdpi.com/algorithms/algorithms-12-00012/article_deploy/html/images/algorithms-12-00012-g004.png - parameters p & q : control how fast the random walk explores!
- these two parameters allow the search to interpolate between BFS & DFS
A. Return parameter, p
- controls the likelihood of “immediately revisiting a node in the walk”
- high p -> less likely to sample the pre-visited nodes ( in the following two steps )
- low p -> keep the walk “local” close to the starting node
B. In-out parameter, q
- allows the search to differentiate between ‘inward & outward’ nodes
- q > 1 : to nodes close to node ‘t’
- q < 1 : get further from node ‘t’ => encourages exploration
(3) node2vec algorithm
 </a>
</a>
