node2vec implementation
- with Football dataset
Football dataset은 11개의 그룹으로 나누어진 115개의 node로 이루어진 network이다. 이 node들 간의 인접 정보를 활용하여 node2vec을 구현하여, 2차원 평면상에 이들의 원래 연결관계가 잘 유지되도록 표현하는 것이 최종 목표이다.
( node2vec에 대해 아직 잘 모른다면, xxx를 참고하라 )
1. Import Dataset & Libraries
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from tqdm import tqdm
%matplotlib inline
H = nx.read_gml('football.gml')
A : 인접 행렬 ( 1: 연결, 0 : 연결X )
A = nx.to_numpy_matrix(H,nodelist=H.nodes())
2. Define functions
1) sigmoid
- 시그모이드 함수
def sigmoid(x):
return 1/(1+np.exp(-x))
2) pos_list & neg_list : getting the positive & negative nodes
- pos_list : 특정 노드 x를 입력 시, 이와 인접한 노드들의 index값 반환
- neg_list : 특정 노드 x를 입력 시, 이와 인접하지 않은 노드들의 index값 반환
def pos_list(node):
return np.nonzero(A[node])[1]
def neg_list(node):
return np.where(A[node]==0)[1]
3) next_choice : choosing the next step according to the transition probability, considering the previous state
- (1) previous : ‘t’ ( 현재 node에서 있기 “직전 node”의 index )
- (2) now : ‘v’ ( 현재 node의 index )
- (3) next : ‘x’ ( 현재 node에서 앞으로 이동할 “다음 node”의 index )
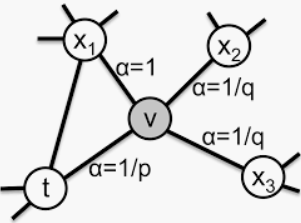
def next_choice(v,t,p,q):
positive = pos_list(v)
li = np.array([])
for pos in positive:
if pos==t:
li = np.append(li,1/p)
elif pos in pos_list(t):
li = np.append(li,1)
else :
li = np.append(li,1/q)
prob = li/li.sum()
return np.random.choice(positive,1,p=prob)[0]
4) random_step : getting the random step, using next_choice
- “3)”에서 정의한 transition probability에 따라, num_walk만큼의 random walk을 뛴다.
def random_step(v,num_walk,p,q):
t = np.random.choice(pos_list(v)) # (1) previous
walk_list = [v]
for _ in range(num_walk):
x = next_choice(v,t,p,q)
walk_list.append(x)
v = x
t = v
return walk_list
3. node2vec
- 위에서 구현한 함수들을 바탕으로 node2vec을 구현한다.

def node2vec(dim,num_epoch,length,lr,k,p,q,num_neg):
embed = np.random.random((A.shape[0],dim))
for epoch in range(num_epoch):
for v in np.arange(A.shape[0]):
walk = random_step(v,length-1,p,q) # (1) random walk
for idx in range(length-k):
not_neg_list = np.append(walk[max(0,idx-k):idx+k],pos_list(walk[idx]))
neg_list = list(set(np.arange(A.shape[0])) - set(not_neg_list))
random_neg = np.random.choice(neg_list,num_neg,replace=False)
for pos in range(idx+1,idx+k+1):
if walk[idx]!=walk[pos]:
pos_embed = embed[walk[pos]]
embed[walk[idx]] -= lr * (sigmoid(np.dot(embed[walk[idx]],pos_embed))-1) * pos_embed
for neg in random_neg:
neg_embed = embed[neg]
embed[walk[idx]] -= lr * (sigmoid(np.dot(embed[walk[idx]],neg_embed))) * neg_embed
return embed
4. Result
- dim (축소시키고 싶은 목표 차원) : 2
- epoch (에폭) : 50
- length (random walk의 길이) : 8
- lr (학습률) : 0.02
- k (context window size) : 2
- p & q : (BFS,DFS 정도를 결정하는 parameter) : 2 & 2
- num_neg (sampling할 negative sample의 개수) : 5
embed = node2vec(dim=2,num_epoch=50,length=8,lr=0.02,
k=2,p=2,q=2,num_neg=5)
def visualize(Emb):
Emb_df = pd.DataFrame(Emb)
Emb_df['Label'] = dict(H.node('value')).values()
Emb_df.loc[Emb_df.Label==0,'Color']='#F22F2F'
Emb_df.loc[Emb_df.Label==1,'Color']='#F5A913'
Emb_df.loc[Emb_df.Label==2,'Color']='#F5F513'
Emb_df.loc[Emb_df.Label==3,'Color']='#8BF513'
Emb_df.loc[Emb_df.Label==4,'Color']='#8DBA5A'
Emb_df.loc[Emb_df.Label==5,'Color']='#25FDFD'
Emb_df.loc[Emb_df.Label==6,'Color']='#25A7FD'
Emb_df.loc[Emb_df.Label==7,'Color']='#1273B3'
Emb_df.loc[Emb_df.Label==8,'Color']='#8E12B3'
Emb_df.loc[Emb_df.Label==9,'Color']='#EBCAF5'
Emb_df.loc[Emb_df.Label==10,'Color']='#D468C2'
Emb_df.loc[Emb_df.Label==11,'Color']='#1C090D'
plt.scatter(Emb_df[0],Emb_df[1],c=Emb_df['Color'])
return Emb_df
embedded = visualize(embed)
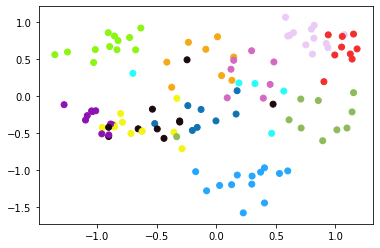
- 2차원 공간상에 그 형태를 잘 유지한 채로 dimension이 축소된 것을 확인할 수 있다! ( 기존 : 115차원 -> now : 2차원 )
pd.DataFrame(embedded).to_csv('Football_embedded_node2vec.csv')
