Chapter 16. Graph pooling DIFFPOOL
( 참고 : https://www.youtube.com/watch?v=JtDgmmQ60x8&list=PLGMXrbDNfqTzqxB1IGgimuhtfAhGd8lHF )
##
1. Graph Prediction
Graph마다 1개의 label이 존재하고, 이를 예측하는 task
GCN update equation :
- \(\mathbf{X}^{t+1}=\operatorname{GConv}\left(\boldsymbol{A}, \boldsymbol{X}^{t}, \mathbf{W}^{t}\right) \quad t=1, \ldots, k\).
Notation
- \(\operatorname{GPool}\left(\mathbf{X}^{k}\right)\) : Global POOLING function
- \(O(\mathbf{W}, \mathbf{g})\) : Graph Readout function
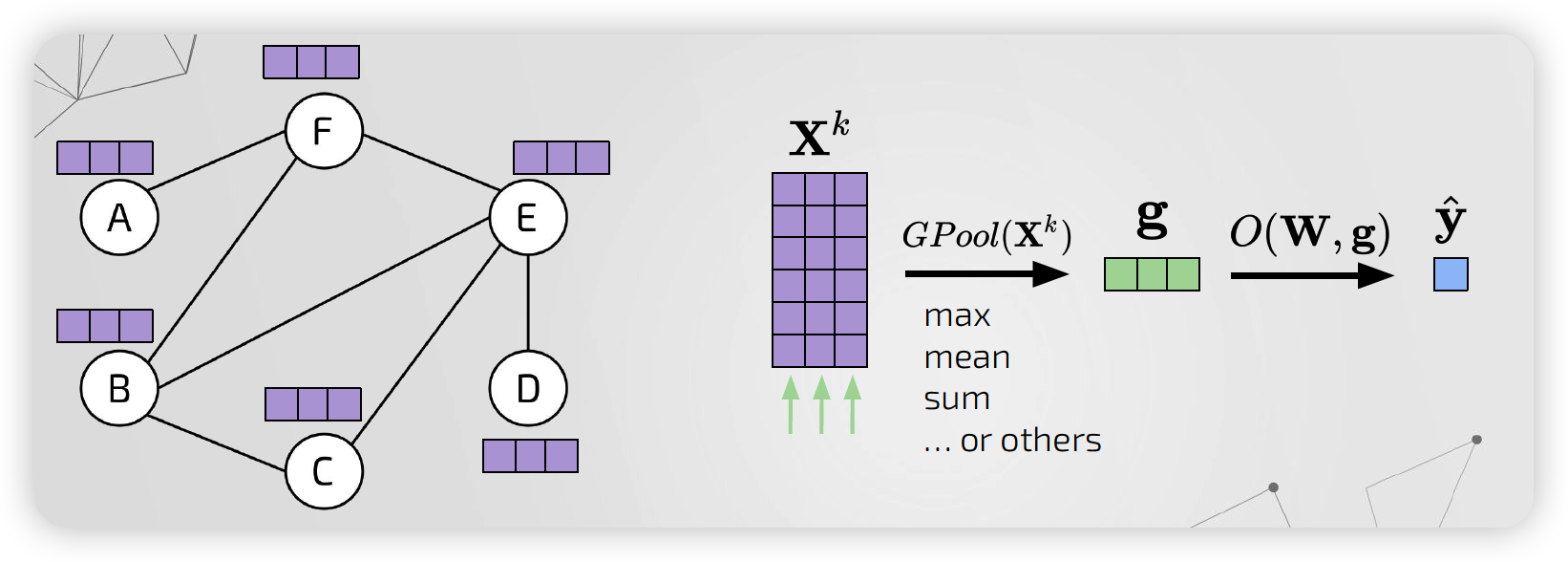
위의 그림을 보면, 노드 벡터들이 모아져서 그래프 벡터가 생성된다.
이는 마치 “그래프 전체의 특징을 대변하는 하나의 가상 super node”로 생각할 수 있다.
하지만, 단순히 모든 노드를 pooling하는 것은, hierarchical 구조를 잡아내지 못한다!!!
\(\rightarrow\) 이를 해결하기 위해 등장한 DIFFPOOL ( = Hierarchical Nodes Pooling Strategy )
2. DIFFPOOL
DIFFPOOL = Differentiable Pooling
- 그래프의 Hierarchical representation을 계산한다
- HOW? by aggregating CLOSE nodes
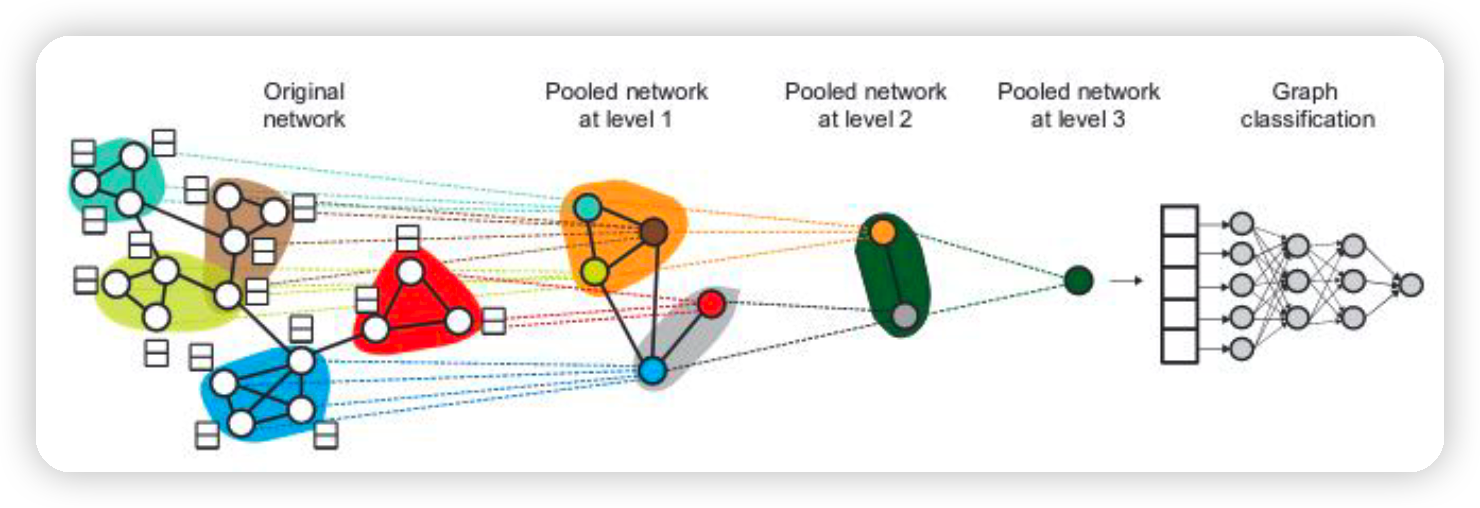
(1) Idea
- 여러 GNN & Pooling layer를 쌓자(stack)!
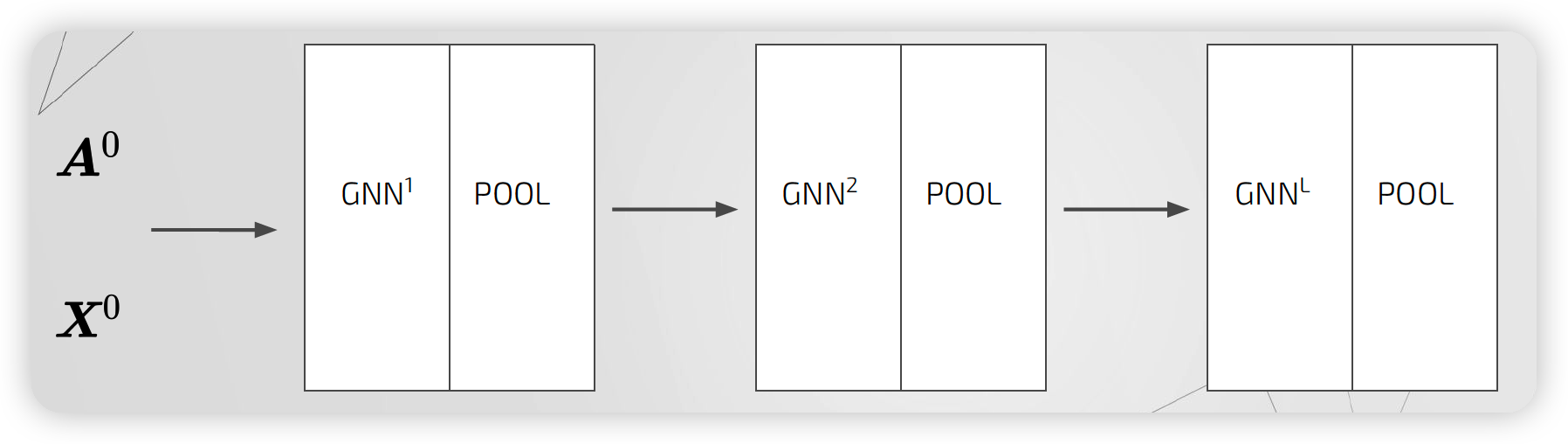
(2) Details
-
데이터 : \(\boldsymbol{D}=\left\{\left(\boldsymbol{G}_{1}, y_{1}\right), \ldots,\left(\boldsymbol{G}_{n}, y_{n}\right)\right)\)
- 그래프 : \(G=(\boldsymbol{A}, \boldsymbol{X})\)
-
모델 : \(\mathbf{Z}=\mathbf{G N N}\left(\boldsymbol{A}, \boldsymbol{X}^{t}, \boldsymbol{W}^{t}\right)\)
- Updating Equation : \(\boldsymbol{X}^{t+1}=\operatorname{GConv}\left(\boldsymbol{A}, \boldsymbol{X}^{t}, \boldsymbol{W}^{t}\right)\)
coarse representation of graph
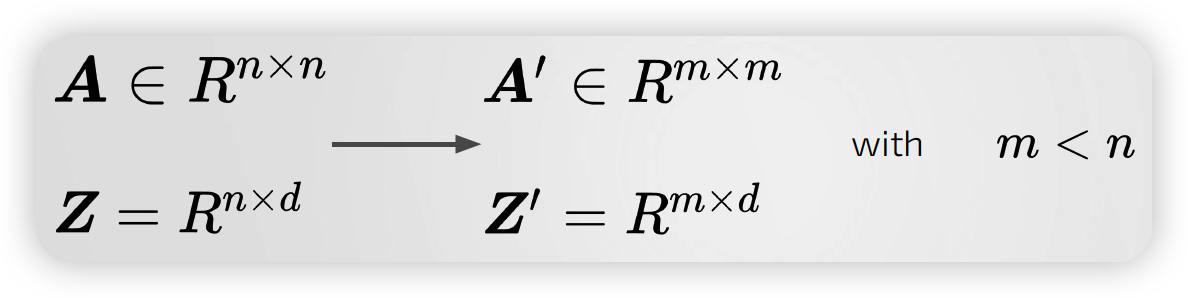
- 개별 노드를 clustering 하자!
그래프를 \(L\) 번 hierarchical step 거침으로써, 최종 representation이 생성된다
- 매 step마다, cluster assignment matrix가 학습된다!
(3) Cluster assignment matrix
Cluster assignment matrix : \(\boldsymbol{S}^{l} \in \boldsymbol{R}^{n^{l} \times n^{l+1}}\)
\[\begin{aligned} \boldsymbol{X}^{l+1} &=\boldsymbol{S}^{l^{T}} \boldsymbol{Z}^{l} \longrightarrow R^{n^{l+1} \times n^{l+1}}\\ \boldsymbol{A}^{l+1} &=\boldsymbol{S}^{l^{T}} \boldsymbol{A} \boldsymbol{S}^{l} \longrightarrow R^{n^{l+1} \times d} \end{aligned}\]- \(\boldsymbol{n}^{l+1}\) : (\(l+1\) step에서의) 클러스터 개수
- \(\boldsymbol{n}^{l}\) : (\(l\) step에서의) 클러스터 개수
- \(\boldsymbol{n}^{0}\) : node 개수
( 클러스터 개수는 hyperparameter 이다 )
위 matrix를 학습하는 방법
\[\begin{aligned} &Z^{l}=\mathrm{GNN}_{\mathrm{emb}}^{l}\left(\boldsymbol{A}^{l}, \boldsymbol{X}^{l}\right) \\ &\boldsymbol{S}^{l}=\operatorname{softmax}\left(\mathrm{GNN}_{\text {pool }}^{l}\left(\boldsymbol{A}^{l}, \boldsymbol{X}^{l}\right)\right) \\ &\mathrm{GNN}_{\text {pool }}^{l} \stackrel{\text { outputs }}{\longrightarrow} R^{n^{l} \times n^{l+1}} \end{aligned}\]- softmax는 미분 가능 & 각 cluster에 속할 확률을 반환
(4) 최종 예측
final output : \(\hat{y}=\operatorname{MLP}( Z^{L})\)
loss function : \(E=L(y, \hat{y})\)
3. DIFFPOOL 코드
(1) Import Packages
import os.path as osp
from math import ceil
import torch
import torch.nn.functional as F
from torch_geometric.datasets import TUDataset
import torch_geometric.transforms as T
from torch_geometric.data import DenseDataLoader
from torch_geometric.nn import DenseGCNConv as GCNConv, dense_diff_pool
(2) Generate dummy data
Node Feature matrix & Adjacency matrix
# Node features matrix
n_nodes = 50
n_features = 32
x_0 = torch.rand(n_nodes, n_features)
adj_0 = torch.rand(n_nodes,n_nodes).round().long()
identity = torch.eye(n_nodes)
adj_0 = adj_0 + identity # self-loop 더하기
(3) Hyperparameters 설정
n_clusters_0 = n_nodes
n_clusters_1 = 5
(4) Embedding 초기화
-
w_gnn_emb: \(Z^{l}=\mathrm{GNN}_{\mathrm{emb}}^{l}\left(\boldsymbol{A}^{l}, \boldsymbol{X}^{l}\right)\) -
w_gnn_pool: \(\boldsymbol{S}^{l}=\operatorname{softmax}\left(\mathrm{GNN}_{\text {pool }}^{l}\left(\boldsymbol{A}^{l}, \boldsymbol{X}^{l}\right)\right)\)
hidden_dim =16
w_gnn_emb = torch.rand(n_features, hidden_dim)
w_gnn_pool = torch.rand(n_features, n_clusters_1)
(5) Embedding 연산 이후
Layer 0
z_0 = torch.relu(adj_0 @ x_0 @ w_gnn_emb)
# (50,50) x (50,32) x (32,16) = (50,16)
s_0 = torch.softmax(torch.relu(adj_0 @ x_0 @ w_gnn_pool), dim=1)
# (50,50) x (50,32) x (32,5) = (50,5)
print(z_0.shape)
print(s_0.shape)
torch.Size([50, 16]) # (n_nodes )
torch.Size([50, 5])
Layer 1
x_1 = s_0.t() @ z_0
# (50,5)' x (50,16) = (5,16)
adj_1 = s_0.t() @ adj_0 @ s_0
# (50,5)' x (50,50) x (50,5) = (5,5)
print(x_1.shape)
print(adj_1.shape)
torch.Size([5, 16])
torch.Size([5, 5])
4. DIFFPOOL 코드 (2)
(1) Import Dataset
max_nodes = 150
class MyFilter(object):
def __call__(self, data):
return data.num_nodes <= max_nodes
dataset = TUDataset('data', name='PROTEINS', transform=T.ToDense(max_nodes),
pre_filter=MyFilter())
dataset = dataset.shuffle()
# 32개의 node (X)
# 32개의 graph (O)
batch_size = 32
n = (len(dataset) + 9) // 10
test_dataset = dataset[:n]
val_dataset = dataset[n:2 * n]
train_dataset = dataset[2 * n:]
test_loader = DenseDataLoader(test_dataset, batch_size=32)
val_loader = DenseDataLoader(val_dataset, batch_size=32)
train_loader = DenseDataLoader(train_dataset, batch_size=32)
(2) Data Overview
for i in train_loader:
print(i)
break
DataBatch(y=[32, 1], mask=[32, 150], x=[32, 150, 3], adj=[32, 150, 150])
(3) Vanilla GNN
class GNN(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels,
n_layers, normalize=False, lin=True):
super(GNN, self).__init__()
self.convs = torch.nn.ModuleList()
self.convs.append(GCNConv(in_channels, hidden_channels, normalize))
for i in range(n_layers-1):
self.convs.append(GCNConv(hidden_channels, hidden_channels, normalize))
self.convs.append(GCNConv(hidden_channels, out_channels, normalize))
self.bns = torch.nn.ModuleList()
for i in range(n_layers):
self.bns.append(torch.nn.BatchNorm1d(hidden_channels))
self.bns.append(torch.nn.BatchNorm1d(out_channels))
def forward(self, x, adj, mask=None):
batch_size, num_nodes, in_channels = x.size()
for layer_idx in range(len(self.convs)):
x = self.bns[layer_idx](F.relu(self.convs[layer_idx](x, adj, mask)))
return x
(4) DIFFPOOL
class DiffPool(torch.nn.Module):
def __init__(self):
super(DiffPool, self).__init__()
#---------------------------------------------#
input_dim = dataset.num_features
output_dim = dataset.num_classes
hidden_dim = 64
n_layers = 2
#---------------------------------------------#
num_cluster1 = ceil(0.25 * max_nodes)
num_cluster2 = ceil(0.25 * 0.25 * max_nodes)
#---------------------------------------------#
self.gnn1_embed = GNN(input_dim, hidden_dim, hidden_dim,
n_layers)
self.gnn2_embed = GNN(hidden_dim, hidden_dim, hidden_dim,
n_layers, lin=False)
self.gnn3_embed = GNN(hidden_dim, hidden_dim, hidden_dim,
n_layers, lin=False)
#---------------------------------------------#
self.gnn1_pool = GNN(input_dim, hidden_dim, num_cluster1,
n_layers)
self.gnn2_pool = GNN(hidden_dim, hidden_dim, num_cluster2,
n_layers)
#---------------------------------------------#
self.lin1 = torch.nn.Linear(hidden_dim, hidden_dim)
self.lin2 = torch.nn.Linear(hidden_dim, output_dim)
#---------------------------------------------#
def forward(self, x0, adj0, mask=None):
# s : cluster assignment matrix
s0 = self.gnn1_pool(x0, adj0, mask)
z0 = self.gnn1_embed(x0, adj0, mask)
x1, adj1, l1, e1 = dense_diff_pool(z0, adj0, s0, mask)
# dense_diff_pool : 아래의 연산을 수행
#x_1 = s_0.t() @ z_0
#adj_1 = s_0.t() @ adj_0 @ s_0
s1 = self.gnn2_pool(x1, adj1)
z1 = self.gnn2_embed(x1, adj1)
x2, adj2, l2, e2 = dense_diff_pool(z1, adj1, s1)
z2 = self.gnn3_embed(x2, adj2)
graph_vec = z2.mean(dim=1)
graph_vec = F.relu(self.lin1(graph_vec))
graph_vec = self.lin2(graph_vec)
return F.log_softmax(graph_vec, dim=-1), l1 + l2, e1 + e2
(5) Train & Validation
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = DiffPool().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
Loss function : negative log likelihood ( y= 0 /1의 binary 값 )
def train(epoch):
model.train()
loss_all = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output, _, _ = model(data.x, data.adj, data.mask)
loss = F.nll_loss(output, data.y.view(-1))
loss.backward()
loss_all += data.y.size(0) * loss.item()
optimizer.step()
return loss_all / len(train_dataset)
@torch.no_grad()
def test(loader):
model.eval()
correct = 0
for data in loader:
data = data.to(device)
pred = model(data.x, data.adj, data.mask)[0].max(dim=1)[1]
correct += pred.eq(data.y.view(-1)).sum().item()
return correct / len(loader.dataset)
