Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

[ 10. Knowledge Graph Embeddings ]

( 참고 : CS224W: Machine Learning with Graphs )


Contents

  • 10-1. RGCN (Relational GCN)
  • 10-2. Knowledge Graphs
  • 10-3. Knowledge Graph Completion


Heterogeneous Graphs

will extend “one edge” type to “multiple edge” types


Heterogeneous graphs

  • \(\boldsymbol{G}=(\boldsymbol{V}, \boldsymbol{E}, \boldsymbol{R}, \boldsymbol{T})\).
    • 1) NODES with node types : \(v_{i} \in V\)
    • 2) EDGES with relation types : \(\left(v_{i}, r, v_{j}\right) \in E\)
    • 3) NODE TYPE : \(T\left(v_{i}\right)\)
    • 4) RELATION TYPE : \(r \in R\)


Heterogeneous graphs models :

  • 1) Relational GCNs
  • 2) Knowledge Graphs
  • 3) Embeddings for KG Completion


10-1. RGCN (Relational GCN)

Heterogeneous graphs

  • multiple edges
  • multiple relation types

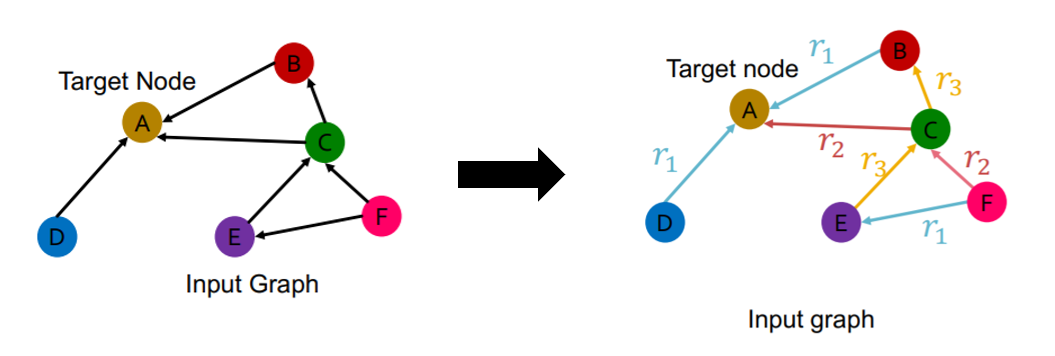
figure2


Solution :

  • use different NN for different relation types

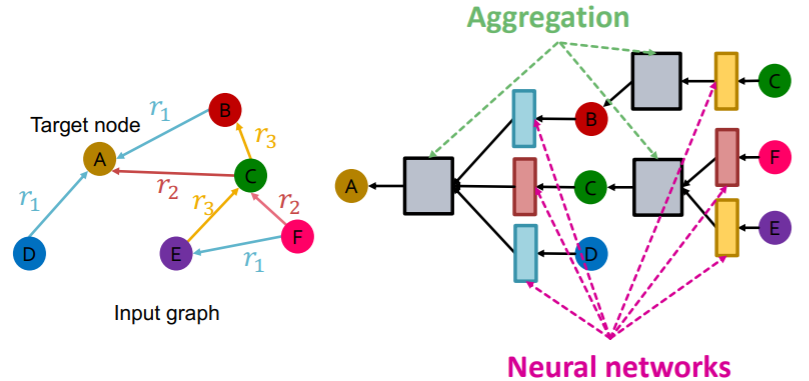
figure2


Relational GCN :

\(\mathbf{h}_{v}^{(l+1)}=\sigma\left(\sum_{r \in R} \sum_{u \in N_{v}^{r}} \frac{1}{c_{v, r}} \mathbf{W}_{r}^{(l)} \mathbf{h}_{u}^{(l)}+\mathbf{W}_{0}^{(l)} \mathbf{h}_{v}^{(l)}\right)\).

  • where \(c_{v, r}=\mid N_{v}^{r} \mid\)


decompose as “Message + Aggregation”

  • 1) Message :
    • 1-1) neighbor : \(\mathbf{m}_{u, r}^{(l)}=\frac{1}{c_{v, r}} \mathbf{W}_{r}^{(l)} \mathbf{h}_{u}^{(l)}\).
    • 1-2) self loop : \(\mathbf{m}_{v}^{(l)}=\mathbf{W}_{0}^{(l)} \mathbf{h}_{v}^{(l)}\).
  • 2) Aggregation :
    • \(\mathbf{h}_{v}^{(l+1)}=\sigma\left(\operatorname{Sum}\left(\left\{\mathbf{m}_{u, r}^{(l)}, u \in N(v)\right\} \cup\left\{\mathbf{m}_{v}^{(l)}\right\}\right)\right)\).


Scalability of RGCN

  • number of layers : \(L\)

  • each relation has \(L\) matrices : \(\mathbf{W}_{r}^{(1)}, \mathbf{W}_{r}^{(2)} \cdots \mathbf{W}_{r}^{(L)}\)

    • dimension of \(\mathbf{W}_{r}^{(l)}\) is \(d^{(l+1)} \times d^{(l)}\)

    • overfitting issue! how to solve?

  • solution : regularize \(\mathbf{W}_{r}^{(l)}\)

    • 1) block diagonal matrices
    • 2) basis/dictionary learning


(1) Block Diagonal Matrices

Use block diagonal matrices for \(\mathbf{W}_{r}^{}\)

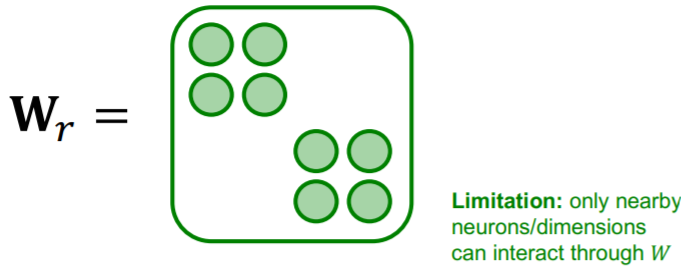
figure2


if we use \(B\) low-dim matrices… number of params will becom

  • before ) \(d^{(l+1)} \times d^{(l)}\)
  • after ) \(B \times \frac{d^{(l+1)}}{B} \times \frac{d^{(l)}}{B}\)


(2) Basis Learning

Share weights across different relations!

Matrix = “linear combination” of “basis” transformation

  • \(\mathbf{W}_{r}=\sum_{b=1}^{B} a_{r b} \cdot \mathbf{V}_{b}\).

    • \(\mathbf{V}_{b}\) : basis matrices ( shared across all relations )

    • \(a_{r b}\) : importance weight of matrix \(\mathbf{V}_{b}\)

    • \(B\) : number of basis to use

  • thus, only need to learn \(\left\{a_{r b}\right\}_{b=1}^{B}\)


(3) Example : Node Classification

  • goal : predict the class of node \(A\), from \(k\) classes

  • final layer (prediction head) :

    \(\mathbf{h}_{A}^{(L)} \in \mathbb{R}^{k}\) = probability of each classes

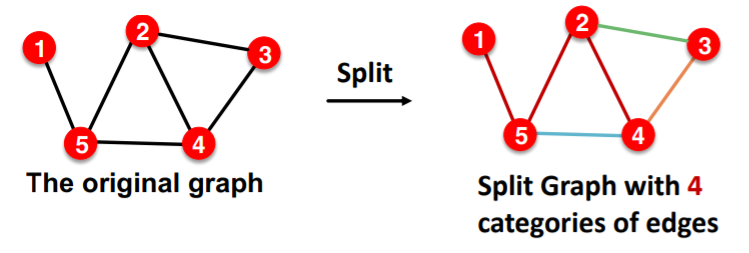
figure2


(4) Example : Link Prediction

Stratified Split….with 4 categories of edges

  • 1-1) [TRAIN] message edges
  • 1-2) [TRAIN] supervision edges
  • 2) [VALIDATION] edges
  • 3) [TEST] edges


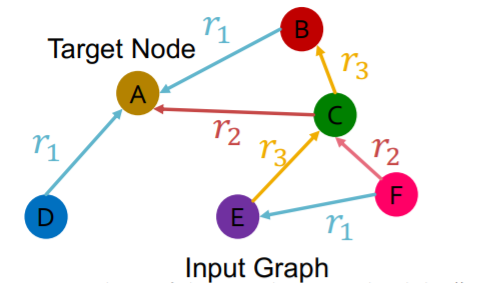
figure2


Example )

  • training message edges : all others

  • training supervision edge : (\(E , r_3, A\) )

    \(\rightarrow\) score this edge

    • final layer of \(E\) : \(\mathbf{h}_{E}^{(L)}\)

    • final layer of \(A\) : \(\mathbf{h}_{A}^{(L)}\)

    • score function : \(f_{r}: \mathbb{R}^{d} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)

    • final score

      = \(f_{r_{1}}\left(\mathbf{h}_{E}, \mathbf{h}_{A}\right)=\mathbf{h}_{E}^{T} \mathbf{W}_{r_{1}} \mathbf{h}_{A}, \mathbf{W}_{r_{1}} \in \mathbb{R}^{d \times d}\)


Training Procedure :

step 1) use RGCN to score “training supervision edge”

  • ex) \(\left(E, r_{3}, A\right)\)

step 2) create negative edge by perturbing supervision edge

  • ex) \(\left(E, r_{3}, B\right), \left(E, r_{3}, D\right)\)
  • note that negative edges should also NOT BELONG to TRAINING MESSAGE EDGES!

step 3) use GNN model to score negative edges

step 4) optimize CE loss

  • \[\ell=-\log \sigma\left(f_{r_{3}}\left(h_{E}, h_{A}\right)\right)-\log \left(1-\sigma\left(f_{r_{3}}\left(h_{E}, h_{B}\right)\right)\right)\]
    • (1) maximize “training supervision edge”
    • (2) minimize “negative edge”


Evaluation Procedure

Example :

  • validation edge : \((E,r_3,D)\)

  • score of “validation edge” should be higher than

    \((E,r_3,v)\) , where it is NOT in the training message/supervision edges


Procedure :

step 1) calculate the score of \((E,r_3,D)\)

step 2) calculate score of all negative edges \(\left\{\left(E, r_{3}, v\right) \mid v \in\{B, F\}\right\}\)

step 3) obtain ranking (RK) of \((E,r_3,D)\)

step 4) calculate metrics

  • 1) Hits@k = \(1[RK \neq k]\)
  • 2) Reciprocal Rank = \(1/RK\)


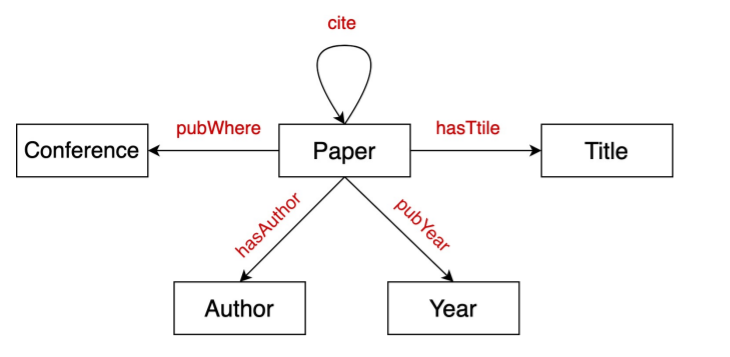
10-2. Knowledge Graphs

Knowledge in graph form

  • nodes : ENTITIES
  • label of nodes : TYPES
  • edges : RELATIONSHIPS

KG(Knowledge Graph) is an example of heterogeneous graph


Example )

figure2


10-3. Knowledge Graph Completion

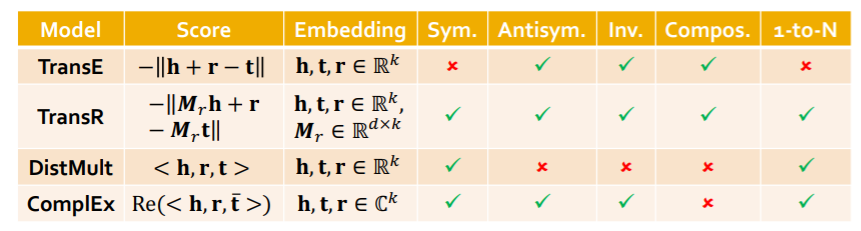
Models

  • 1) TransE
  • 2) TransR
  • 3) DistMul
  • 4) ComplEx


(1) KG Completion Task

task : for a given (HEAD, RELATION), predict “missing tails”

Example )

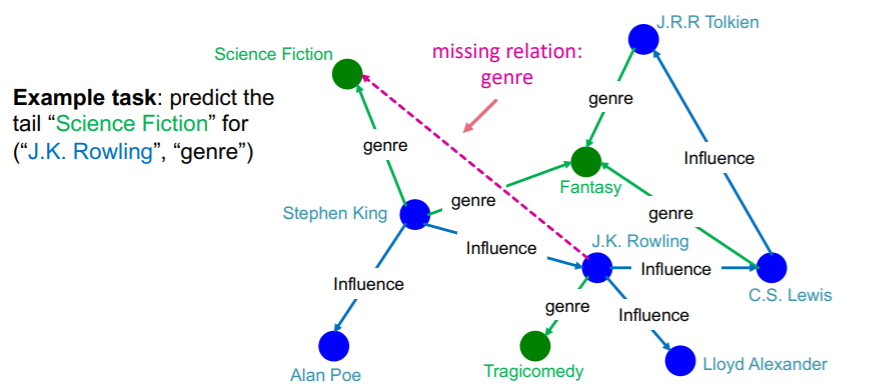
figure2


Notation

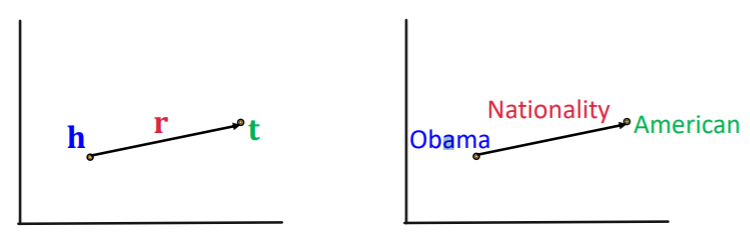
  • edges are represented as triples \((h,r,t)\)
    • \(h\) : head
    • \(r\) : relation
    • \(t\) : tail
  • given \((h,r,t)\), make embedding \((h,r)\) to be close to embedding \(t\)
    • Q1) how to embed?
    • Q2) how to define closeness?


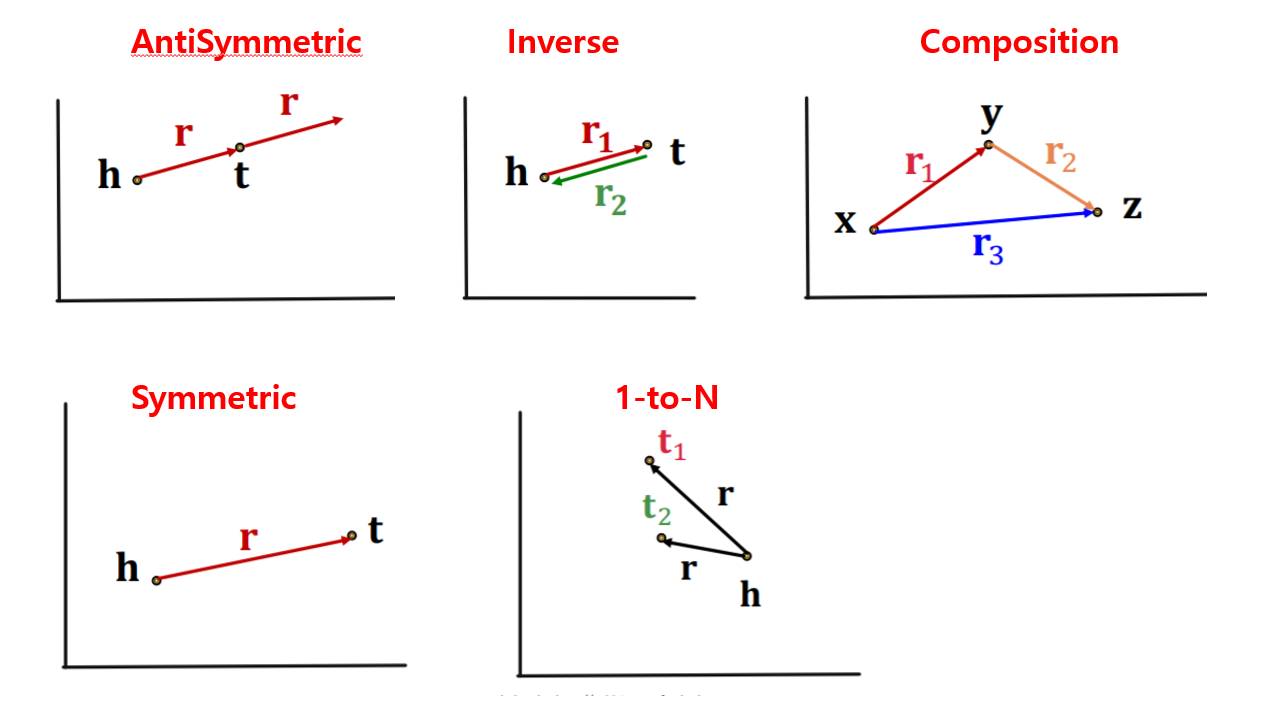
(2) Connectivity Patterns in KG

  1. Symmetric :

    • notation : \(r(h, t) \Rightarrow r(t, h)(r(h, t) \Rightarrow \neg r(t, h)) \quad \forall h, t\)
    • example : roommate
  2. Inverse :
    • notation : \(r_{2}(h, t) \Rightarrow r_{1}(t, h)\).
    • example : (advisor, advisee)
  3. Composition (Transitive)
    • notation : \(r_{1}(x, y) \wedge r_{2}(y, z) \Rightarrow r_{3}(x, z) \quad \forall x, y, z\).
    • example : (mother’s husband = father)
  4. 1-to-N
    • notation : \(r\left(h, t_{1}\right), r\left(h, t_{2}\right), \ldots, r\left(h, t_{n}\right) \text { are all True. }\)
    • example : r = StudentsOf


(3-1) TransE

  • idea : \(\mathbf{h}+\mathbf{r} \approx \mathbf{t}\)
  • scoring function : \(f_{r}(h, t)=- \mid \mid \mathbf{h}+\mathbf{r}-\mathbf{t} \mid \mid\)
  • loss : max margin loss


figure2


Relation Types

  • Antisymmetric (O)

    • \(h+r=t\), but \(t+r \neq h\)

  • Inverse (O)

    • \(h + r_2 =t\), we can set \(r_1 = -r_2\)

  • Composition (O)

    • \[r_3 = r_1 + r_2\]

  • Symmetric (X)

    • only if \(r=0\), \(h=t\)

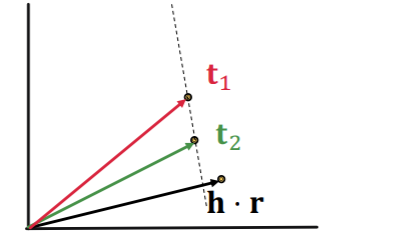
  • 1-to-N (X)

    • \(t_1\) and \(t_2\) will map same vector

      although they are different entities

    • contradictory!

      • \[t_1 = h+r = t_2\]
      • \[t_1 \neq t_2\]

figure2


(3-2) TransR

TransE :

  • translation of any relation in the SAME embedding space


TransR :

  • translation of relation in the DIFFERENT embedding space
  • notation
    • model “entities” as vectors in the entity space \(\mathbb{R}^{d}\)
    • model “each relation” as vector in relation space \(\mathbf{r} \in \mathbb{R}^{k}\)
      • with \(\mathbf{M}_{r} \in \mathbb{R}^{k \times d}\) as projection matrix


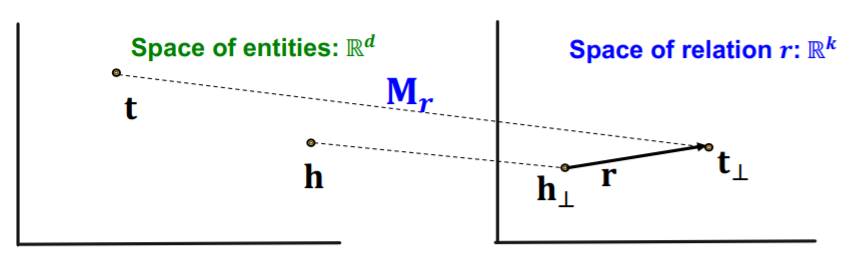
figure2

  • \(\mathbf{h}_{\perp}=\mathbf{M}_{r} \mathbf{h}, \mathbf{t}_{\perp}=\mathbf{M}_{r} \mathbf{t}\).
  • score function : \(f_{r}(h, t)=-\left \mid \mid \mathbf{h}_{\perp}+\mathbf{r}-\mathbf{t}_{\perp}\right \mid \mid\)


Relation Types

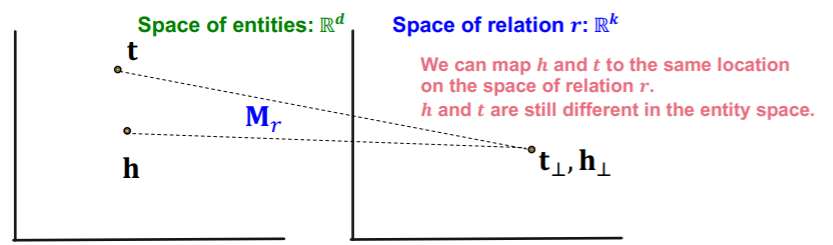
  • Symmetric (O)

    • \(\mathbf{r}=0, \mathbf{h}_{\perp}=\mathbf{M}_{r} \mathbf{h}=\mathbf{M}_{r} \mathbf{t}=\mathbf{t}_{\perp}\).
    • figure2

  • Assymetric (O)

    • \(\mathbf{r} \neq 0, \mathbf{M}_{r} \mathbf{h}+\mathbf{r}=\mathbf{M}_{r} \mathbf{t}\).

      then, \(\mathbf{M}_{r} \mathbf{t}+\mathbf{r} \neq \mathbf{M}_{r} \mathbf{h}\)

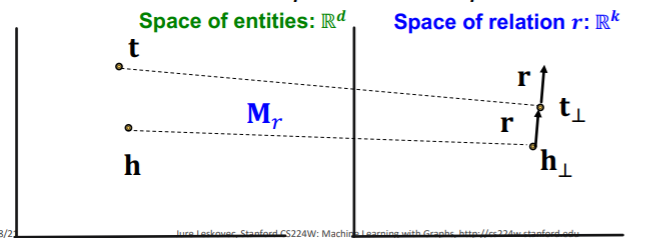
    • figure2

  • 1-to-N (O)
    • we can learn \(\mathbf{M}_{r}\) so that \(\mathbf{t}_{\perp}=\mathbf{M}_{r} \mathbf{t}_{1}=\mathbf{M}_{r} \mathbf{t}_{2}\)
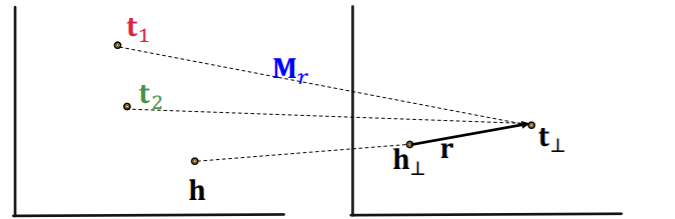
    • figure2

  • Inverse (O)

    • \[\mathbf{r}_{2} =-\mathbf{r}_{1}, \mathbf{M}_{r_{1}}=\mathbf{M}_{r_{2}}\]

      then, \(\mathbf{M}_{r_{1}} \mathbf{t}+\mathbf{r}_{1} =\mathbf{M}_{r_{1}} \mathbf{h} \text { and } \mathbf{M}_{r_{2}} \mathbf{h}+\mathbf{r}_{2}=\mathbf{M}_{r_{2}} \mathbf{t}\)

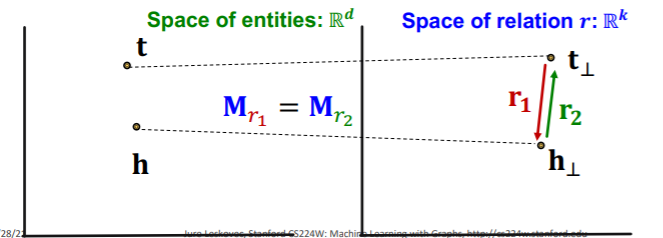
    • figure2
  • Composition (O)


(3-3) DistMult

  • adopt BILINEAR modeling!

  • score function : \(f_{r}(h, t)=<\mathbf{h}, \mathbf{r}, \mathbf{t}>=\sum_{i} \mathbf{h}_{i} \cdot \mathbf{r}_{i} \cdot \mathbf{t}_{i}\).

    • can be seen as cosine similarity, between \(h\cdot r\) & \(t\)

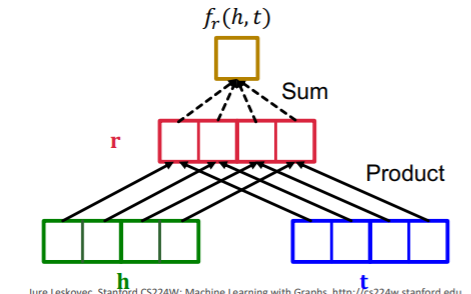
figure2


Relation Types

  • 1-to-N (O)
    • \(\left\langle\mathbf{h , r}, \mathbf{t}_{1}\right\rangle=\left\langle\mathbf{h}, \mathbf{r}, \mathbf{t}_{2}\right\rangle\).
    • figure2
  • Symmetric (O)
    • \(f_{r}(h, t)=<\mathbf{h}, \mathbf{r}, \mathbf{t}>=\sum_{i} \mathbf{h}_{i} \cdot \mathbf{r}_{i} \cdot \mathbf{t}_{i}=<\mathbf{t}, \mathbf{r}, \mathbf{h}>=f_{r}(t, h)\).

  • AntiSymmetric (X)

    • \(f_{r}(h, t)=<\mathbf{h}, \mathbf{r}, \mathbf{t}>=<\mathbf{t}, \mathbf{r}, \mathbf{h}>=f_{r}(t, h)\).

      ( \(r(h,t)\) & \(r(t,h)\) will always have same score )

  • Inverse (X)

    • \(f_{r_{2}}(h, t)=\left\langle\mathbf{h}, \mathbf{r}_{2}, \mathbf{t}\right\rangle=\left\langle\mathbf{t}, \mathbf{r}_{1}, \mathbf{h}\right\rangle=f_{r_{1}}(t, h)\).

      ( this means \(\mathbf{r}_{2}=\mathbf{r}_{1}\) )

  • Composition (X)

    • union of the hyperplane induced by multi-hops of relations

      can not be expressed using a single hyperplane!


(3-4) ComplEx

  • based on DistMult
  • embeds entities&relations in COMPLEX vector space

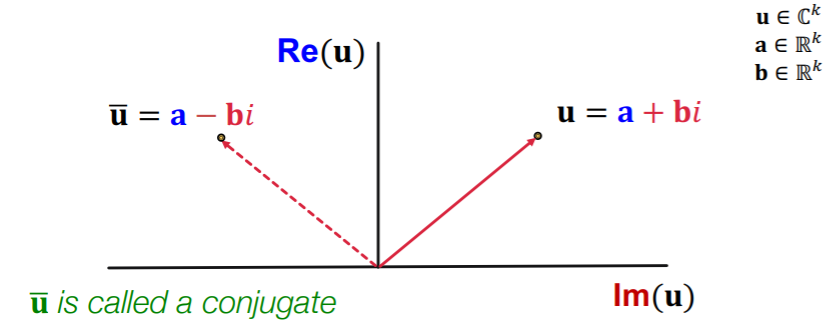
figure2


  • Score function : \(f_{r}(h, t)=\operatorname{Re}\left(\sum_{i} \mathbf{h}_{i} \cdot \mathbf{r}_{i} \cdot \overline{\mathbf{t}}_{i}\right)\).

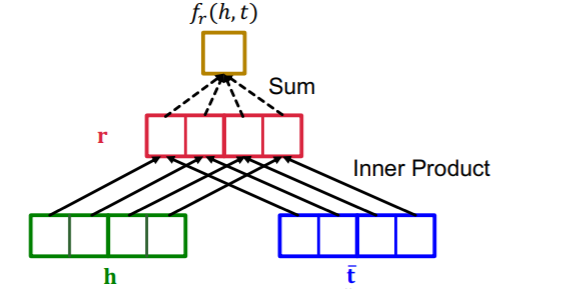
figure2


Relation Types

  • Antisymmetric (O)
    • High \(f_{r}(h, t)=\operatorname{Re}\left(\sum_{i} \mathbf{h}_{i} \cdot \mathbf{r}_{i} \cdot \overline{\mathbf{t}}_{i}\right)\).
    • Low \(f_{r}(t, r)=\operatorname{Re}\left(\sum_{i} \boldsymbol{t}_{i} \cdot \mathbf{r}_{i} \cdot \overline{\boldsymbol{h}}_{i}\right)\)
  • Symmetric (O)
    • when \(Im(r)=0\)….
    • \(\begin{aligned} f_{r}(h, t)&=\operatorname{Re}\left(\sum_{i} \mathbf{h}_{i} \cdot \mathbf{r}_{i} \cdot \overline{\mathbf{t}}_{i}\right)=\sum_{i} \operatorname{Re}\left(\mathbf{r}_{i} \cdot \mathbf{h}_{i} \cdot \overline{\mathbf{t}}_{i}\right) \\ &=\sum_{i} \mathbf{r}_{i} \cdot \operatorname{Re}\left(\mathbf{h}_{i} \cdot \overline{\mathbf{t}}_{i}\right)=\sum_{i} \mathbf{r}_{i} \cdot \operatorname{Re}\left(\overline{\mathbf{h}}_{i} \cdot \mathbf{t}_{i}\right)\\&=\sum_{i} \operatorname{Re}\left(\mathbf{r}_{i} \cdot \overline{\mathbf{h}}_{i} \cdot \mathbf{t}_{i}\right)=f_{r}(t, h) \end{aligned}\).
  • Inverse (O)
    • \(\mathbf{r}_{1}=\overline{\mathbf{r}}_{2}\).
    • Complex conjugate of \(\mathbf{r}_{2}=\underset{\mathbf{r}}{\operatorname{argmax}} \operatorname{Re}(<\mathbf{h}, \mathbf{r}, \overline{\mathbf{t}}>)\) is exactly \(\mathbf{r}_{1}=\underset{\mathbf{r}}{\operatorname{argmax}} \operatorname{Re}(<\mathbf{t}, \mathbf{r}, \overline{\mathbf{h}}>)\).
  • Composition (X)
  • 1-to-N (O)


(3-5) Summary

figure2

Tags: ,

Categories:

Updated:

You May Also Enjoy

2 minute read

2 minute read

8 minute read

2 minute read