5. Graph Recurrent Networks (GRNs)
5-1. GGNN (Gated GNN)
-
use GRU in propagation step
-
unrolls the RNN for a fixed number of \(T\) Steps & BPTT
Basic recurrence :
- aggregation
- \[\mathbf{a}_{v}^{t} =\mathbf{A}_{v}^{T}\left[\mathbf{h}_{1}^{t-1} \ldots \mathbf{h}_{N}^{t-1}\right]^{T}+\mathbf{b}\]
-
GRU update
-
\(\begin{aligned}\mathbf{z}_{v}^{t} &=\sigma\left(\mathbf{W}^{z} \mathbf{a}_{v}^{t}+\mathbf{U}^{z} \mathbf{h}_{v}^{t-1}\right) \\ \mathbf{r}_{v}^{t} &=\sigma\left(\mathbf{W}^{r} \mathbf{a}_{v}^{t}+\mathbf{U}^{r} \mathbf{h}_{v}^{t-1}\right) \\ \widetilde{\mathbf{h}}_{v}^{t} &=\tanh \left(\mathbf{W} \mathbf{a}_{v}^{t}+\mathbf{U}\left(\mathbf{r}_{v}^{t} \odot \mathbf{h}_{v}^{t-1}\right)\right) \\ \mathbf{h}_{v}^{t} &=\left(1-\mathbf{z}_{v}^{t}\right) \odot \mathbf{h}_{v}^{t-1}+\mathbf{z}_{v}^{t} \odot \widetilde{\mathbf{h}}_{v}^{t} \end{aligned}\).
-
use information from
- (1) node’s neighbors
- (2) previous timestep
-
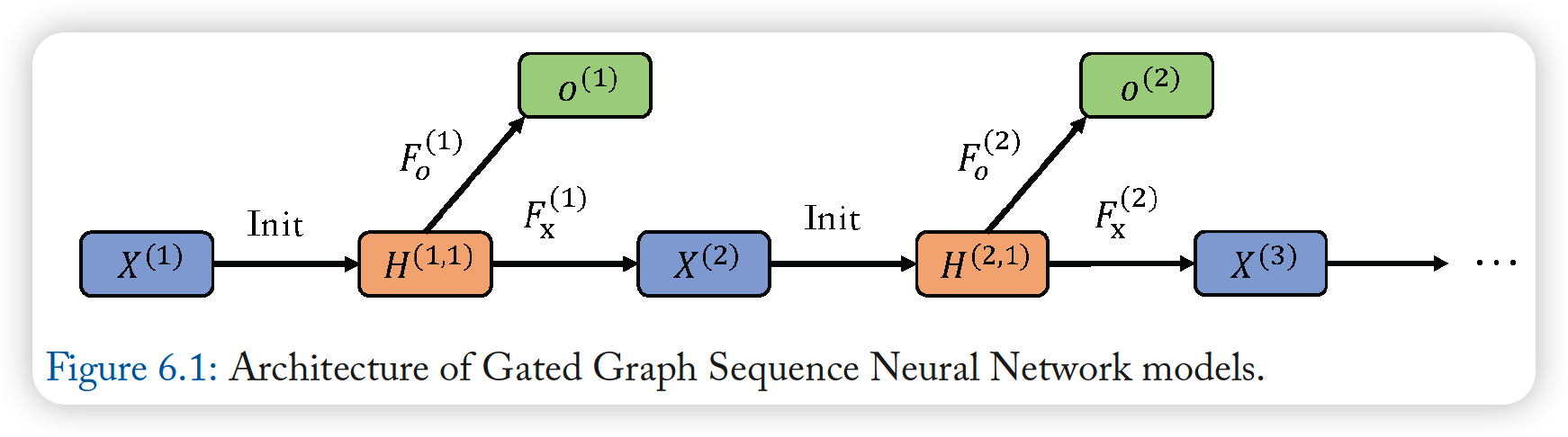
GGS-NNs (Gated Graph Sequence NN)
- uses several GGNNs, to produce an output sequence \(\mathbf{o}^{(1)} \ldots \mathbf{o}^{(K)}\)
example) 2 GGNNs are used
5-2. Tree LSTM
2 extensions of LSTM
- (1) Child-Sum Tree-LSTM
- (2) N-ary Tree-LSTM
Tree-LSTM
- (like standard LSTM), contains..
- (1) \(\mathbf{i}_{v}\) : input gate
- (2) \(\mathbf{o}_{v}\) : output gate
- (3) \(\mathbf{c}_{v}\) : memory cell
- (4) \(\mathbf{h}_{v}\) : hidden state
-
forget gate
-
use one (X)
-
use forget gate \(\mathbf{f}_{v k}\) for each child \(k\)
( allow node \(v\) to aggregate information from its child )
-
(1) Child-Sum Tree-LSTM
\(\begin{aligned} \widetilde{\mathbf{h}}_{v}^{t-1} &=\sum_{k \in N_{v}} \mathbf{h}_{k}^{t-1} \\ \mathbf{i}_{v}^{t} &=\sigma\left(\mathbf{W}^{i} \mathbf{x}_{v}^{t}+\mathbf{U}^{i} \widetilde{\mathbf{h}}_{v}^{t-1}+\mathbf{b}^{i}\right) \\ \mathbf{f}_{v k}^{t} &=\sigma\left(\mathbf{W}^{f} \mathbf{x}_{v}^{t}+\mathbf{U}^{f} \mathbf{h}_{k}^{t-1}+\mathbf{b}^{f}\right) \\ \mathbf{o}_{v}^{t} &=\sigma\left(\mathbf{W}^{o} \mathbf{x}_{v}^{t}+\mathbf{U}^{o} \widetilde{\mathbf{h}}_{v}^{t-1}+\mathbf{b}^{o}\right) \\ \mathbf{u}_{v}^{t} &=\tanh \left(\mathbf{W}^{u} \mathbf{x}_{v}^{t}+\mathbf{U}^{u} \widetilde{\mathbf{h}}_{v}^{t-1}+\mathbf{b}^{u}\right) \\ \mathbf{c}_{v}^{t} &=\mathbf{i}_{v}^{t} \odot \mathbf{u}_{v}^{t}+\sum_{k \in N_{v}} \mathbf{f}_{v k}^{t} \odot \mathbf{c}_{k}^{t-1} \\ \mathbf{h}_{v}^{t} &=\mathbf{o}_{v}^{t} \odot \tanh \left(\mathbf{c}_{v}^{t}\right), \end{aligned}\).
(2) N-ary Tree-LSTM
-
if # of childern of each node is at most \(K\)
-
And children can be ordered from \(1\) to \(K\)..
\(\rightarrow\) it is N-ary Tree-LSTM
\(\begin{aligned} \mathbf{i}_{v}^{t} &=\sigma\left(\mathbf{W}^{i} \mathbf{x}_{v}^{t}+\sum_{l=1}^{K} \mathbf{U}_{l}^{i} \mathbf{h}_{v l}^{t-1}+\mathbf{b}^{i}\right) \\ \mathbf{f}_{v k}^{t} &=\sigma\left(\mathbf{W}^{f} \mathbf{x}_{v}^{t}+\sum_{l=1}^{K} \mathbf{U}_{k l}^{f} \mathbf{h}_{v l}^{t-1}+\mathbf{b}^{f}\right) \\ \mathbf{o}_{v}^{t} &=\sigma\left(\mathbf{W}^{o} \mathbf{x}_{v}^{t}+\sum_{l=1}^{K} \mathbf{U}_{l}^{o} \mathbf{h}_{v l}^{t-1}+\mathbf{b}^{o}\right) \\ \mathbf{u}_{v}^{t} &=\tanh \left(\mathbf{W}^{u} \mathbf{x}_{v}^{t}+\sum_{l=1}^{K} \mathbf{U}_{l}^{u} \mathbf{h}_{v l}^{t-1}+\mathbf{b}^{u}\right) \\ \mathbf{c}_{v}^{t} &=\mathbf{i}_{v}^{t} \odot \mathbf{u}_{v}^{t}+\sum_{l=1}^{K} \mathbf{f}_{v l}^{t} \odot \mathbf{c}_{v l}^{t-1} \\ \mathbf{h}_{v}^{t} &=\mathbf{o}_{v}^{t} \odot \tanh \left(\mathbf{c}_{v}^{t}\right) \end{aligned}\).
-
separate parameter matrices for each child \(k\)
( more fine-grained reprsentations for each node )
5-3. Graph LSTM
2 types of Tree-LSTM can be adapted to GRAPH!
\(\rightarrow\) Graph structured LSTM
Difference between “graphs” & “trees”
- edges of graphs have LABELS
\(\begin{aligned} \mathbf{i}_{v}^{t} &=\sigma\left(\mathbf{W}^{i} \mathbf{x}_{v}^{t}+\sum_{k \in N_{v}} \mathbf{U}_{m(v, k)}^{i} \mathbf{h}_{k}^{t-1}+\mathbf{b}^{i}\right) \\ \mathbf{f}_{v k}^{t} &=\sigma\left(\mathbf{W}^{f} \mathbf{x}_{v}^{t}+\mathbf{U}_{m(v, k)}^{f} \mathbf{h}_{k}^{t-1}+\mathbf{b}^{f}\right) \\ \mathbf{o}_{v}^{t} &=\sigma\left(\mathbf{W}^{o} \mathbf{x}_{v}^{t}+\sum_{k \in N_{v}} \mathbf{U}_{m(v, k)}^{o} \mathbf{h}_{k}^{t-1}+\mathbf{b}^{o}\right) \\ \mathbf{u}_{v}^{t} &=\tanh \left(\mathbf{W}^{u} \mathbf{x}_{v}^{t}+\sum_{k \in N_{v}} \mathbf{U}_{m(v, k)}^{u} \mathbf{h}_{k}^{t-1}+\mathbf{b}^{u}\right) \\ \mathbf{c}_{v}^{t} &=\mathbf{i}_{v}^{t} \odot \mathbf{u}_{v}^{t}+\sum_{k \in N_{v}} \mathbf{f}_{v k}^{t} \odot \mathbf{c}_{k}^{t-1} \\ \mathbf{h}_{v}^{t} &=\mathbf{o}_{v}^{t} \odot \tanh \left(\mathbf{c}_{v}^{t}\right), \end{aligned}\).
- \(m(v,k)\) : edge label between node \(v\) & \(k\)
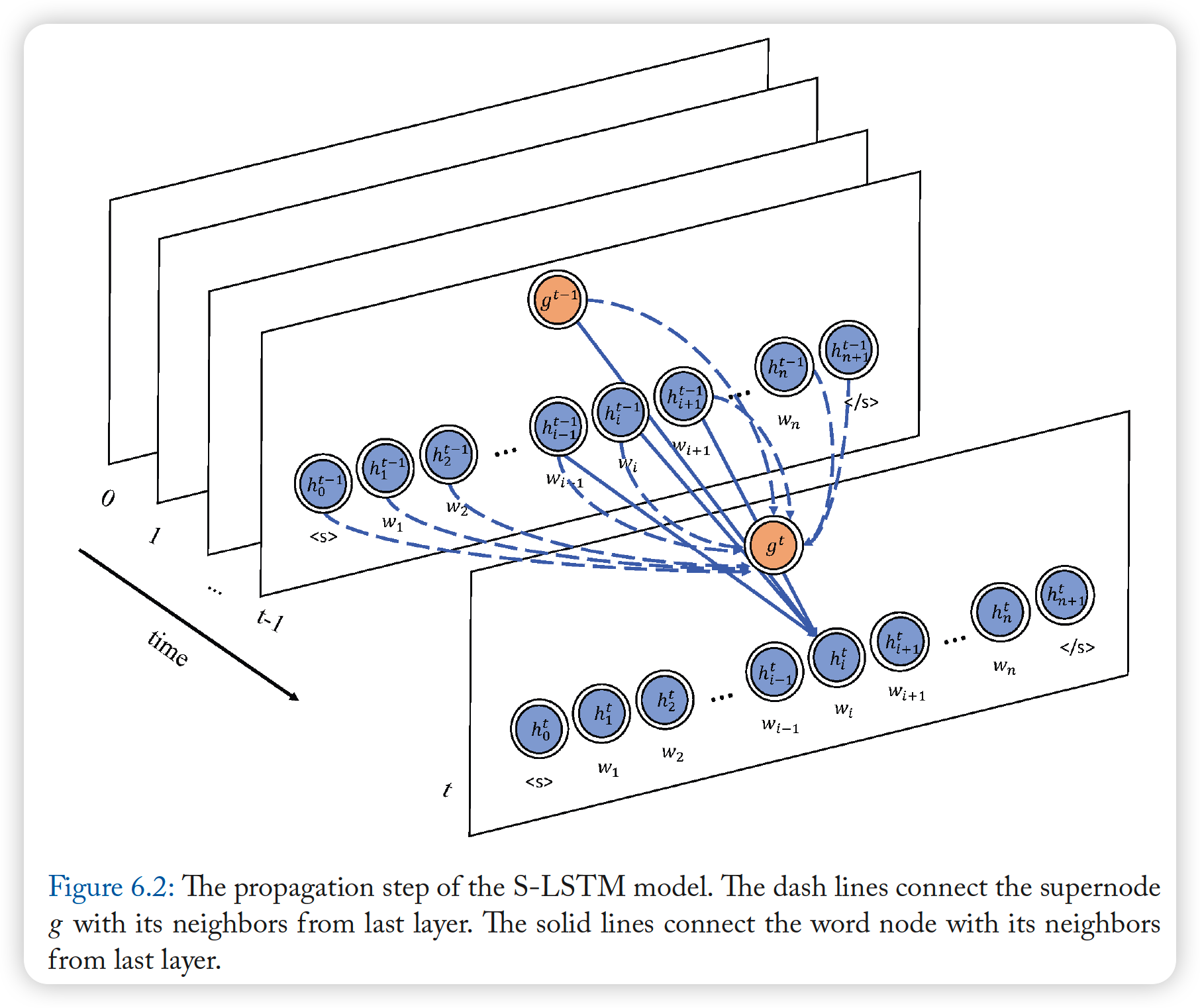
5-4. Sentence LSTM ( S-LSTM )
purpose : text encoding
- converts text into graph
- uses Graph-LSTM to learn representations
Concepts
- node = words
- aggregate informations from neighboring words
- uses super node
- provide GLOBAL information, to solve long-distnace dependency problem
\(\rightarrow\) each word can obtain both (1) local & (2) global information
Sentence Classification
- hidden state of supernode can be used
- outperforms Transformer!