(paper) T-GCN ; A Temporal GCN for Traffic Prediction

T-GCN : A Temporal GCN for Traffic Prediction

0. Abstract

to capture SPATIAL & TEMPORAL dependence simultaneously,

\(\rightarrow\) propose T-GCN

• combination of (1) GCN + (2) GRU

1. Methodology

(1) Problem Definition

Notation

• unweighted graph : \(G=(V, E)\)
  • road nodes : \(V=\left\{v_{1}, v_{2}, \cdots, v_{N}\right\}, \mathrm{N}\)
• adjacency matrix : \(A \in R^{N \times N}\)
• feature matrix : \(X^{N \times P}\)
  • \(P\) : length of historical TS ( = number of node attributes )
  • \(X_{t} \in R^{N \times 1}\) : speed of every road, at time \(t\)

Goal : \(\left[X_{t+1}, \cdots, X_{t+T}\right]=f\left(G ;\left(X_{t-n}, \cdots, X_{t-1}, X_{t}\right)\right)\)

• backcast size : \(n\)
• forecast size : \(T\)

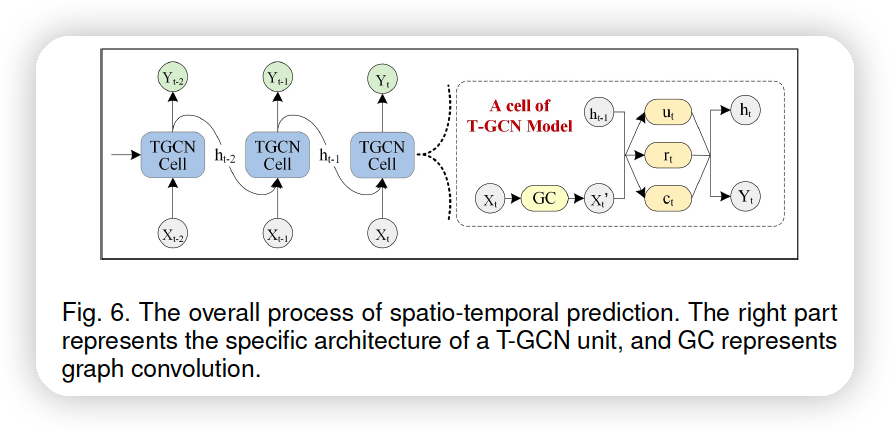
(2) Overview

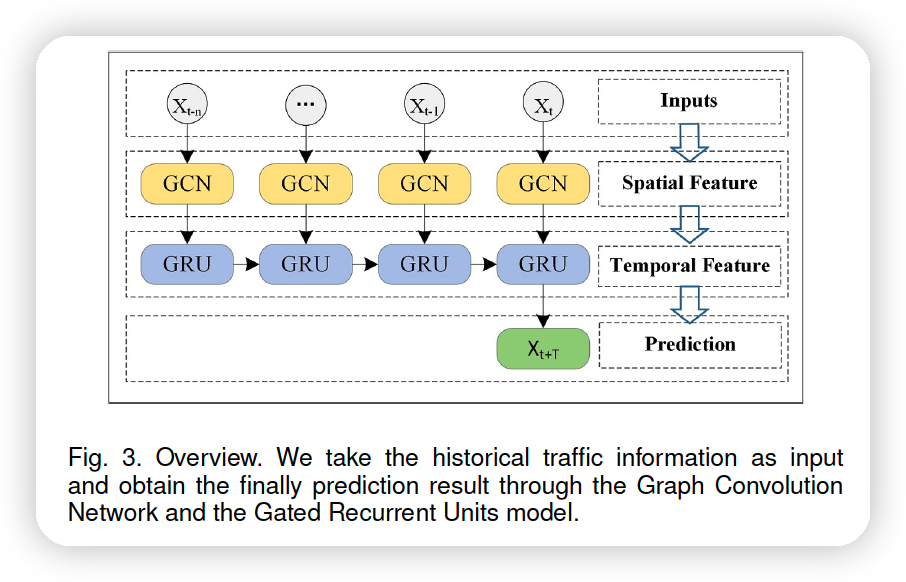
매 time step마다의 input size : \(N \times 1\)

(3) Methodology

a) SPATIAL : GCN

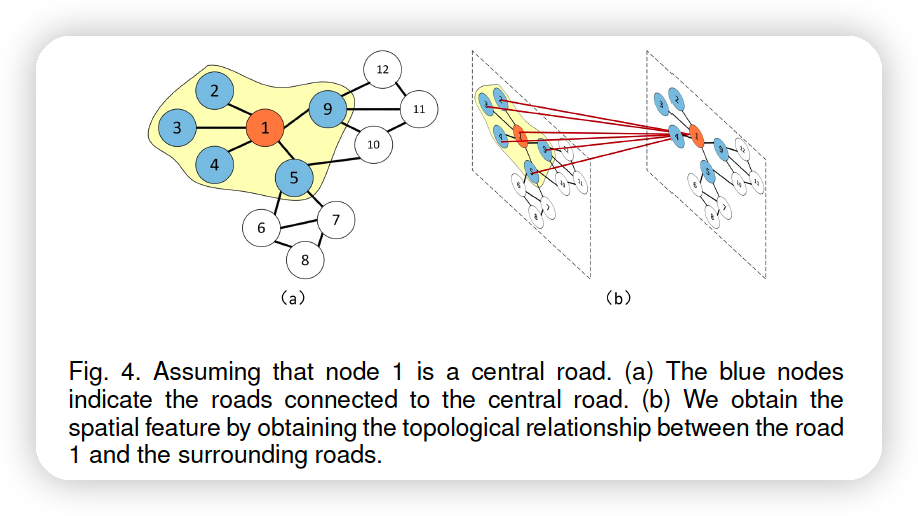
CNN vs GCN

• CNN : only on Euclidean space
• GCN : ok on non-Euclidean space

GCN

• constructs a filter in Fourier Domain
• use GCN to learn spatial features
• \(f(X, A)=\sigma\left(\widehat{A} \operatorname{Relu}\left(\widehat{A} X W_{0}\right) W_{1}\right)\).
  • \(\widehat{A}=\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}{ }^{-\frac{1}{2}}\).
    • \(\widetilde{A}=A+I_{N}\).
    • \(\widetilde{D}=\sum_{j} \widetilde{A}_{i j}\).

b) TEMPORAL : GRU

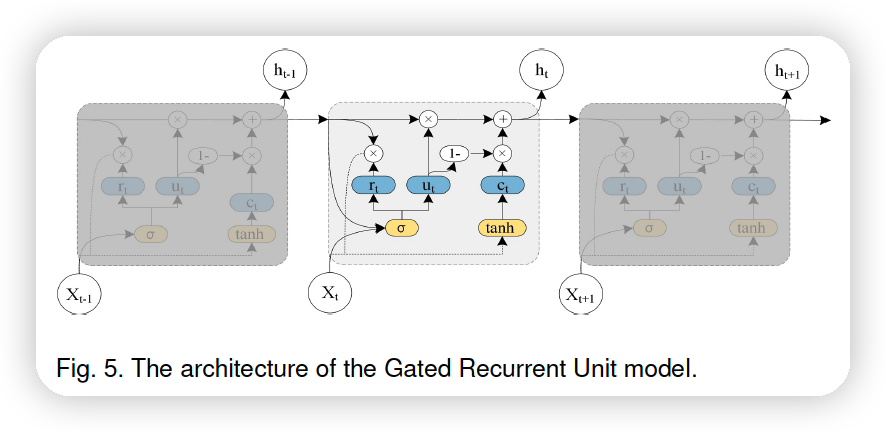
c) T-GCN