[interpretable] (paper 1) Why Should I Trust You? Explaining the Predictions of Any Classifier

“Why Should I Trust You?”

Explaining the Predictions of Any Classifier

Contents

1. Abstract
2. Introduction
3. The Case For Explanations
4. LIME (Locally Interpretable Model-agnostic Explanations)
   1. Interpretable Data Representations
   2. Fidelity-Interpretability Trade-off
   3. Sampling for Local Exploration & Example
   4. Sparse Linear Explanation
   5. Examples
5. SP(Submodular Pick) LIME

0. Abstract

성능 좋은 대부분의 ML/DL모델들은 Black-box model

BUT, 그 내면의 원인 (=어떻게 하여 그러한 결과가 나왔는가?)에 대한 해석은 상당히 중요!

따라서, 이 논문에서는 이를 풀기 위한 LIME (Local Interpretable Model-agnostic Explanations)을 제안!

[ LIME 간단 요약 ]

• key : ANY classifier 설명 가능!
• 방법 : learning an interpretable model, locally around the prediction

1. Introduction

“If the users do not trust a model or a prediction, they will not use it!”

여기서 “믿는다(= trust)”의 의미는?

• 1) trusting a PREDICTION
  • 어떠한 “예측 결과”를 기반으로 한 무언 다른 행동을 할 만한가?
  • ex) “여기 골목에서 좌회전을 하라고 모델은 말하는데, 예측 결과를 믿어도 되겠지..?”
• 2) trusting a MODEL
  • 모델링 끝낸 이후 해당 모델을 배포해서 사용할때, 예상한 대로 모델이 잘 작동할지?
  • ex) 대부분의 ML모델은, evaluation할 때 validation dataset을 사용함. 그런데, real-world data는 이와 다를 수 있다!
  • ex) 애초에 우리가 설정한 loss function이, 우리가 이루고자 하는 goal에 적합하지 않을 수도?

이 논문에서는, 위의 두 trust를 심어주고자 LIME을 제안 함.

• 1) trusting a PREDICTION을 위해서

  \(\rightarrow\) 개별 예측값(individual prediction)에 대한 explanation을 제공하는 것을 목표로 함!

• 2) trusting a MODEL 을 위해서

  \(\rightarrow\) 여러 예측값(multiple predictions)을 선택한다!

Contribution

• 1) LIME = algorithm that explain predictions of ANY CLASSIFIER/REGRESSOR in a faithful way, by approximating it locally

• 2) SP-LIME = method that selects a set of representative instances ( for “trusting the MODEL” )

• 3) experiment 성능 GOOD

2. The Case For Explanations

(1) “Explaining a Prediction”이란?

• “instances’ components” ( ex. text내의 단어, image 내의 patch들 )와,

  “예측 결과”사이의 relationship 파악!

• ML practitioner는 여러 대안 중 특정 model을 선택해야하는 상황에 직면한다.

  따라서 서로 다른 두 모델 사이의 “relative trust”를 평가할 수 있어야 한다!

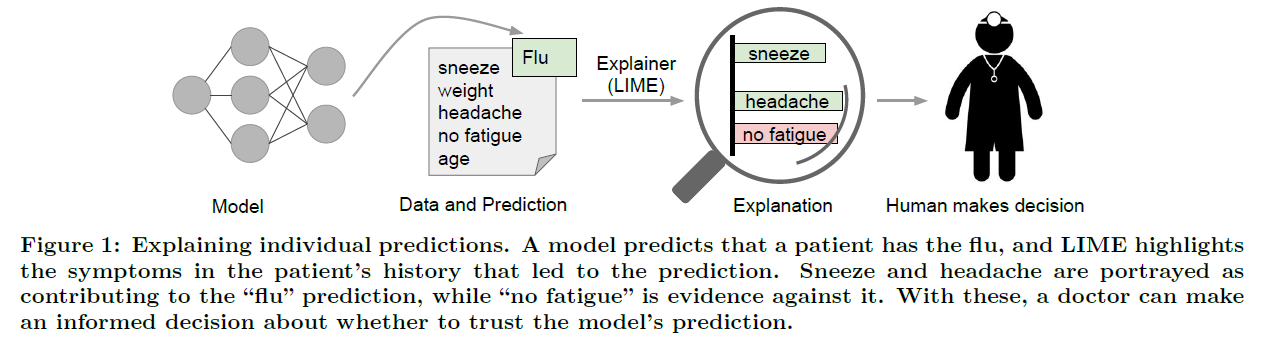
• 1) 모델은 환자가 “감기에 걸렸다”라고 예측을 하고,
• 2) LIME은 그러한 예측의 근거가 되는 증상을 찾아낸다 (highlight)

(2) Desired characteristics for Explainers

Explainers에게 요구되는 특징들

• 1) Interpretable

  • \(X\)와 \(Y\) 사이의 관계를 “정량적으로” 설명할 수 있는가?
  • Linear 모델이라고 반드시 interpretable한 것은 아님!
    • ex) 변수 1000개로 Y를 예측하는 모델…어떠한 것이 Y에 기여했는가? NOT EASY!

• 2) Local Fidelity

  • locally faithful해야!

    ( = 예측하려는 instance 부근(vicinity)의 데이터에서도 비슷하게 예측이 되는지 )

  • globally faithful을 확인하는 것은 complex model에서 여전히 challenge…

• 3) Model-Agnostic

  • ANY 모델에 적용가능해야!

• 4) Global perspective

  • 보다 넓은 관점에서 봐야!
  • ex) classifier에서 accuracy가 전부가 아닐 수 있다. (애초에 적절한 metric이 아닐 수 있다)

3. LIME (Local Interpretable Model-agnostic Explanations)

LIME의 목표

• identify an interpretable model over the interpretable representation that is locally faithful to ANY classifier

3-1. Interpretable Data Representations

( 우선, “Feature”와 “Interpretable data representation”을 잘 구분해야! )

“Interpretable data representation”

• “인간에게 이해 가능한” 표현으로 나타나야함

• example)

  • TEXT : 특정 단어가 있으면 1, 없으면 0
  • VISION : 특정 물체가 있으면 1, 없으면 0

NOTATION :

• \(x \in R^d\) : ORIGINAL representation of an instance being explained
• \(x' \in \{ 0,1\}^{d'}\) : INTERPRETABLE data representation ( binary vector )
• 쉽게 말해, \(x\)의 interpretable version이 \(x'\)이다.
• example)
  • \[x = (0.4, -1.5, 0.1, 0.2, 1.3, -3.5)\]
  • \(x' = (0,0,1,0\))

3-2. Fidelity-Interpretability Trade-off

NOTATION :

• 모델 : \(g \in G\)

• \(G\) : interpretable models의 class

  ( ex. linear model, decision tree, …. )

• \(\Omega(g)\) : complexity of \(g\)

  ( ex. \(g\)가 decision tree라면, \(\Omega(g)\) 는 max depth )

  ( ex. \(g\)가 linear model이라면, \(\Omega(g)\) 는 non-zero weight의 개수 )

• \(f\) : 설명의 대상이 되는 모델

  • \(g\)와 \(f\)의 차이: (헷갈리지 말기)

    • \(g\)는 “해석가능한 모델” ( ex. 선형 모델, decision tree )”

      ( INTEPRETABLE representation이 input으로 들어감 )

    • \(f\)는 “해석하고자하는 모델” ( ex. classification 문제의 경우, \(f(x)\) = probability )

      ( ORIGINAL representation 이 input으로 들어감 )

• \(\pi_x\) : \(z\)와 \(x\) 사이의 proximity measure

  ( \(z\)는 \(x\) 부근에서 샘플된 데이터들! )

• \(L(f,g,\pi_x)\) : measure of how unfaithful \(g\) is in approximating \(f\) in the locality defined by \(\pi_x\)

목표 : 아래의 2가지를 모두 잡는 것!

• 1) “INTERPRETABILITY (해석가능성)”
• 2) “LOCAL FIDELITY (지역적 신뢰도)”

따라서, 그러기 위해 아래의 식을 minimize해야한다!

• \(\xi(x)=\underset{g \in G}{\operatorname{argmin}} \mathcal{L}\left(f, g, \pi_{x}\right)+\Omega(g)\).

3-3. Sampling for Local Exploration & Example

우리는 \(f\)에 대한 어떠한 가정을 하지 않고도, \(L(f,g,\pi_x)\)를 minimize하고자함.

( explainer가 model-agnostic하길 원하니까 )

\(L(f,g,\pi_x)\)를 “근사”한다! HOW? by drawing samples

[ (\(G\)를 Linear model로 가정) Algorithm 요약 ]

1. ( \(x\)의 interpretable representation version인 ) \(x'\) 의 부근에서 여러 sample을 뽑는다 ( = \(z'\) )
2. \(z'\) 를 다시 original representation version인 \(z\)로 되돌린다
3. 이 \(z\)를 사용하여 \(f(z)\)를 계산한다 ( 얘를 일종의 label로 취급 )
4. \(\pi_x(z)\) 계산 한다 ( 즉, \(x\)와 \(z\) 사이의 proximity 계산 )
5. \(\xi(x)=\underset{g \in G}{\operatorname{argmin}} \mathcal{L}\left(f, g, \pi_{x}\right)+\Omega(g)\) 를 optimize

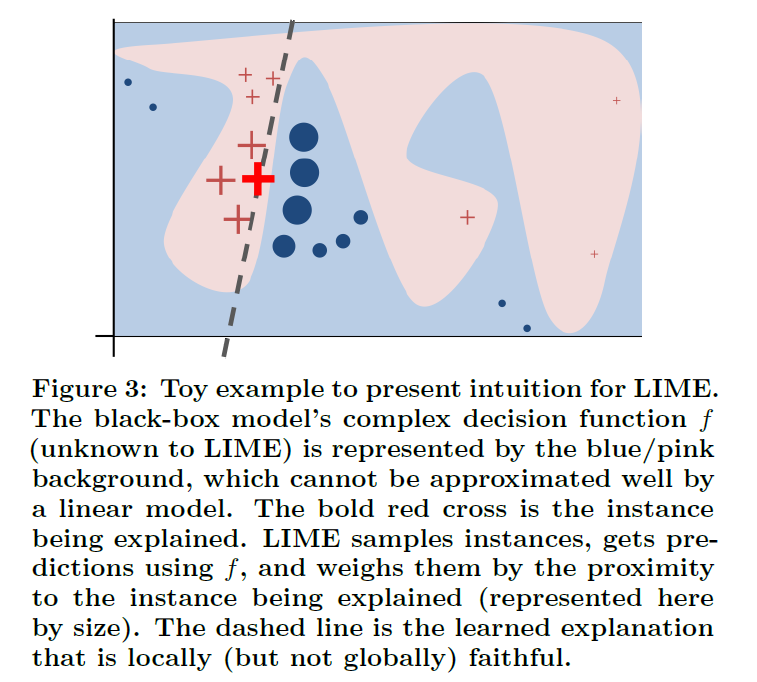
• \(f\) : 위의 pink & blue의 경계선 ( complex decision function )

• 굵은 빨간 십자가 : explain하고자 하는 instance

• 단계

  • step 1) 굵은 빨간 십자가 주변의 여러 instance를 샘플한다 ( 빨간 십자가들 & 파란 점들 )

  • step 2) 위에서 뽑힌 sample들의 \(f(\cdot)\) 값 계산

    ( 가까이 뽑힌 애들은 high weight, 멀리서 뽑힌 애들은 low weight 부여 )

    ( weight가 클 수록 더 큰 size로 표현 )

• 점선 : learned explanation ( locally faithful함 )

3-4. Sparse Linear Explanation

앞으로 \(G\)는 linear model로 한정 시켜서 설명할 것!

• \[g(z')= w_g \cdot z'\]

• locally weighted square loss는 아래와 같이 정의함

  \[L=\sum_{z} \pi_{x}(z)\left(f(z)-g\left(z^{\prime}\right)\right)^{2}\]

• proximity measure는 \(\exp \left(-D(x, z)^{2} / \sigma^{2}\right)\)로 가정

  ( \(D(\cdot, \cdot)\) : distance function …. text의 경우 cosine distance, image의 경우 L2 distance )

앞서 말했 듯, 위의 \(L\)식에다가 complexity term을 더해줘야! ( penalty term 느낌으로 )

Complexity term 예시

• text classification : \(\Omega(g)=\infty \mathbb{1}\left[\left\|w_{g}\right\|_{0}>K\right]\).
  • interpretable representation : bag-of-words
  • \(\Omega(g)\)의 의미 : \(K\) 개를 number of words의 limit으로 설정

3-5 & 3-6. Examples

[ TEXT ]

[IMAGE]

4. SP(Submodular Pick) LIME

LIME : 특정 instance에 대한 설명은 할 수 있음. BUT, model을 trust한다고는 할 수 없다.

SP-LIME = method that selects a set of representative instances ( for “trusting the MODEL” )

즉, LIME은 1개의 instance만을 보고, SP-LIME은 여러 instance들을 봄!

[ 과정 요약 ]

( 어려움…http://shuuki4.github.io/deep%20learning/2016/08/24/Why-Should-I-Trust-You-%EB%85%BC%EB%AC%B8-%EC%A0%95%EB%A6%AC.html 참고 )

• B개의 budget limit을 설정한 뒤, 중요한 feature들이 골라지도록 B개 미만의 test instance를 고르기
  • feature weight : LIME을 사용하여 계산한 interpretable model의 weight의 sqrt 값의 합
• weighted pick cover (NP-HARD)라서, greedy 하게 제일 목표함수값이 높아지는 instance를 선택해 나감
• 사용자는 B개의 instance 설명 결과를 보고 이 model의 행동 방식을 유추할 수 있을 것