[interpretable] (paper 3) Interpretability Beyond Feature Atribution ; Quantitative Testing with Concept Activation Vectors (TCAV)

Interpretability Beyond Feature Atribution : Quantitative Testing with Concept Activation Vectors (TCAV) (2017)

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Interpretability methods
   2. Interpretability methods in NN
   3. Linearity in NN and latent dimensions
4. Methods
   1. User-defined Concepts as Sets of Examples
   2. CAVs ( Concept Activation Vectors )
   3. Directional Derivatives and Conceptual Sensitivity
   4. TCAV ( Testing with CAVs )

0. Abstract

Interpretation of DL = challenging! WHY?

\(\rightarrow\) OPERATE on low-level feature ( not on high-level concept )

Introduce CAVs (Concept Activation Vectors)

• provide an interpretation of NN’s internal state in terms of human-friendly concepts

• key idea : view high-dim internal state of NN as an aid

1. Introduction

Interpretability를 바라보는 대표적인 관점

• describe prediction “in terms of INPUT FEATURES”

이의 문제점?

• 1) 대부분의 ML모델은 주로 feature ( ex. pixel value ) 상에서 operate

  ( \(\neq\) 인간이 이해 가능한 high level concept )

• 2) model’s internal values ( ex. neural activations ) : 너무 incomprehensible

Notation

• state of ML model : \(E_m\) ( spanned by basis vectors \(e_m\) )

• vector space of human : \(E_h\)

  ( 여기서 \(E_h\)는 input feature /training data로 국한되지 않고, user-provided data도 OK )

결국, 우리가 “interpretation”을 한다는 것은, \(g : E_m \rightarrow E_h\)를 찾는 것!

( 여기서 \(g=\) linear일 경우, linear interpretability )

Concept Activation Vector (CAV)

• \(E_m\)과 \(E_h\)를 translate하는 방법
• derive CAVs by training a linear classifier between concept’s examples & random counter examples

quantitative Testing with CAV (TCAV)

• 이 논문의 최종 결과! new linear interpretability method

• use directional derivatives

  to quantify the model prediction’s sensitivity to an underlying HIGH-level concept

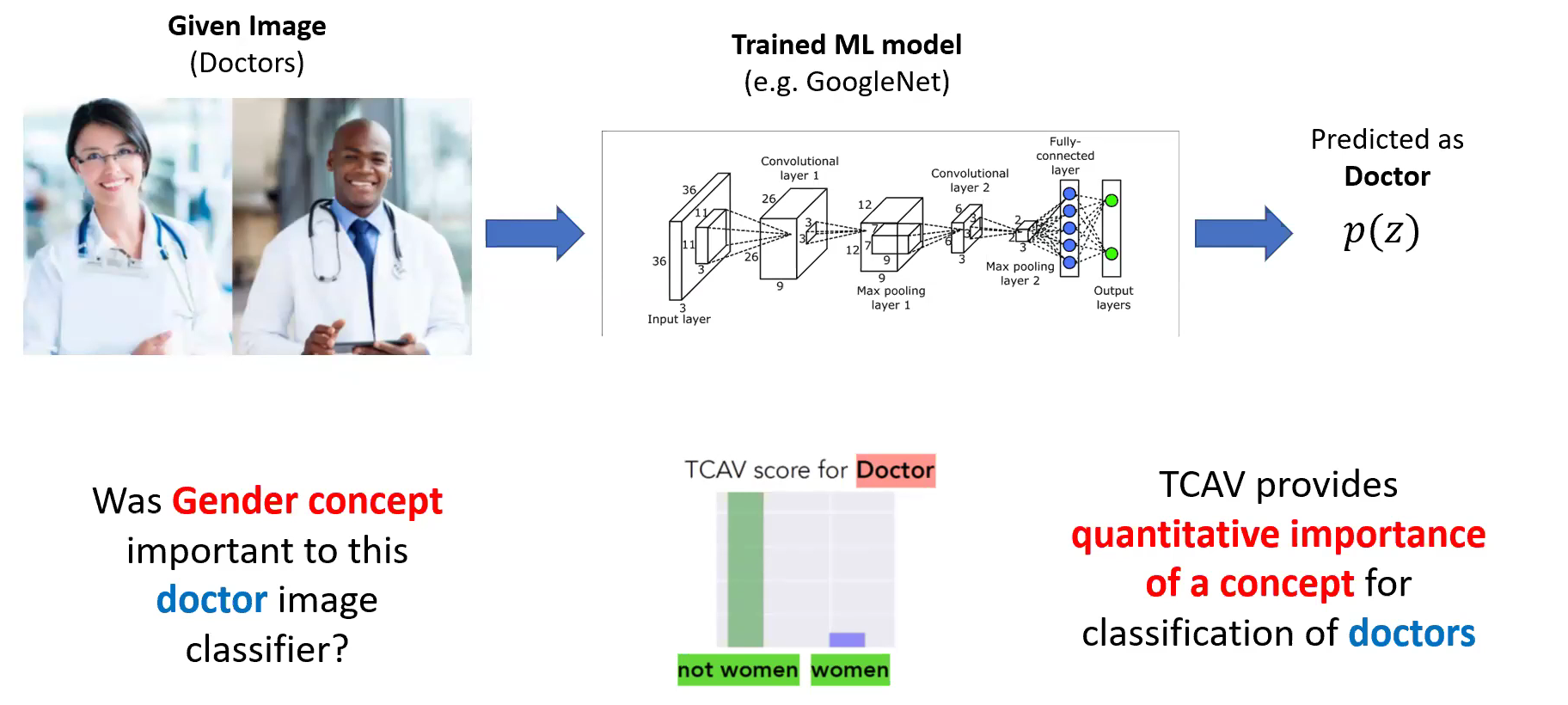
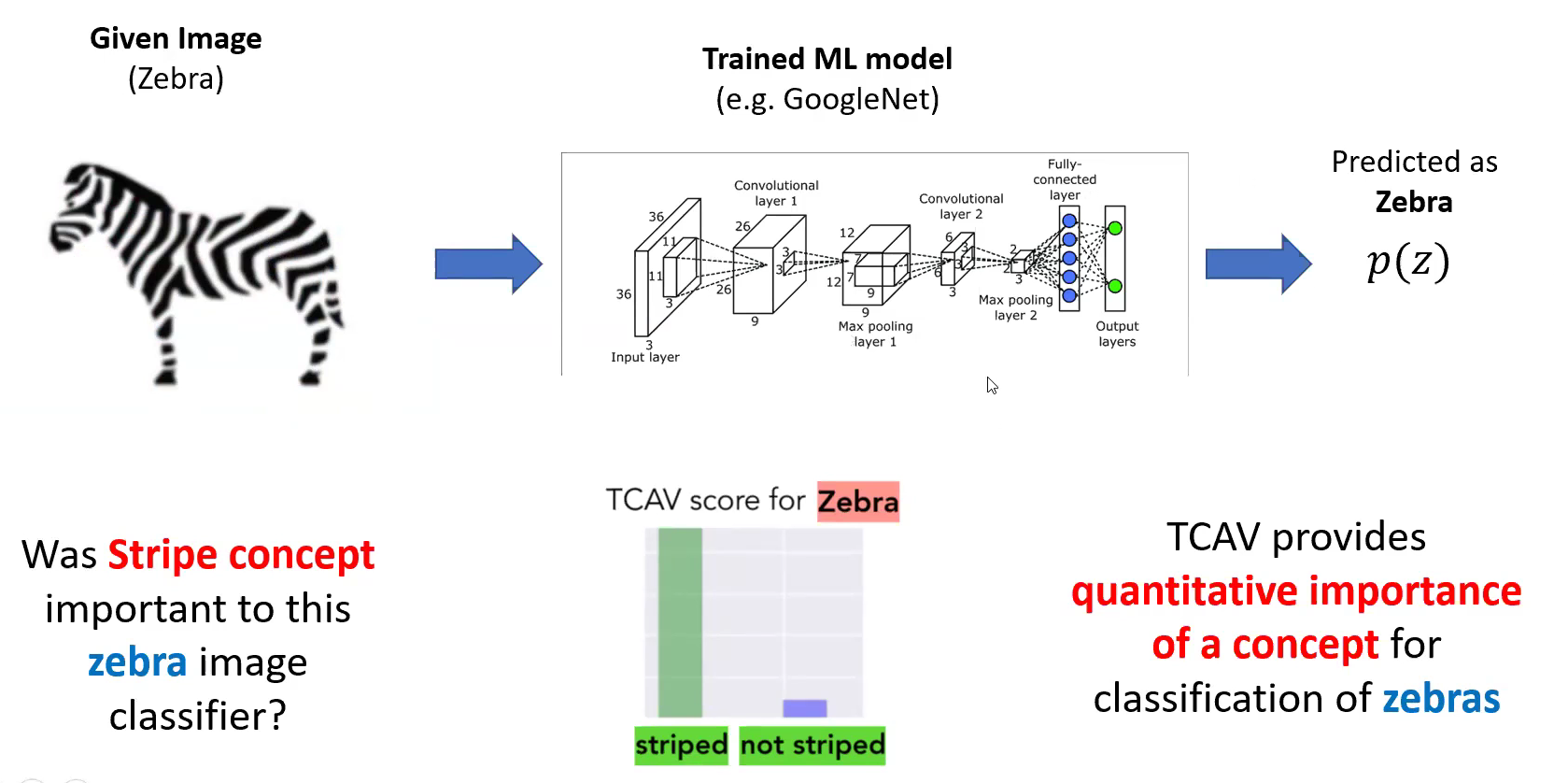
• ex) “얼룩말” 사진

  • user-defined set of examples : “striped” (줄무늬가 있는)
  • TCAV는 “striped”라는 concept이 “얼룩말”이라는 prediction을 낸 영향을 quantify할 수 있다.

TCAV의 goals

• 1) Accessibility : ML 전문가가 아니더라도 OK
• 2) Customization : adapts to ANY concept
• 3) Plug-in readiness : retraining (X)
• 4) Global quantification : interpret ENTIRE CLASSES (O), individual datapoints (X)

2. Related Work

• 2-1) overview of interpretability methods

• 2-2) methods specific to NN
• 2-3) methods that leverage the local linearity of NNs

2-1) Interpretability methods

interpretability를 얻기 위한 2가지 옵션

• [옵션 1] interpretable model로 모델을 국한시키기
  • 어려운 점 ) high performance 어려워
• [옵션 2] 모델을 post-process하여 insight를 얻기
  • 어려운 점 ) ensure the explanation correctly reflects model’s complex internals

interpretability를 얻기 위한 method의 트렌드

• method that can be applied without retraining or without modifying the network

• use generated explanation as input & check network’s output for validation

  ( 주로 perturbation-based / sensitivity analysis-based interpretability methods 에서 사용 )

Perturbation-based

• use data/features as a form of perturbation

  & check response changes

• maintain consistency..

  • 1) locally ( data point & neighbors에서 explanation이 true )

  • 2) globally ( 거의 모은 data point ~ )

    \(\rightarrow\) TCAV는 global perturbation method

2-2) Interpretability methods in NN

TCAV의 목표 : interpret high-dim \(E_m\)

Saliency methods :

• popular local explanation methods for image classification

• produce a map showing how important each pixel is!

Saliency Map :

( 출처 : https://www.youtube.com/watch?v=-y0oghbEHMM&t=1127s )

limitations of Saliency Map

• 1) conditioned on only ONE picture
• 2) users have NO CONTROL over what concepts of interest these maps pick up on
• 3) vulnerable to adversarial attacks

2-3) Linearity in NN and latent dimensions

1) Linear combination of neurons encode meaningful information!

• meaningful directions can be efficiently learned by simple linear classifiers

2) Mapping latent dimensions to human concepts

이 논문의 아이디어

• compute directional derivatives along these learned directions

  ( 각 direction의 importance 확인 위해! )

4. Methods

ideas & methods

• (a) how to use directional derivatives to quantify sensitivity of predictions for different conepts

• (b) how to compute the final quantitative explanation ( without retraining )

  quantitative explanation : 해당 concept이 해당 예측결과를 내는데에 있어서 얼마나 중요한 역할을 했는지 정량화!

  ( 주의 : 여기서 concept은 training 과정이나, label과는 전혀 무관! 아예 모델 train 완료된 이후, 사용하는 개념! )

Notation

• input : \(x \in \mathbb{R}^{n}\)
• feedforward layer \(l\) with \(m\) neurons
• \(f_{l}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\).

Goal of TCAV

( 출처 : https://www.youtube.com/watch?v=-y0oghbEHMM&t=1127s )

3-1) User-defined Concepts as Sets of Examples

[1단계] concept 정의하기!

• find an independent dataset with concept labeled
• 두 종류의 dataset을 구한다
  • 1) concept set과 관련된 dataset ( ex. “줄무늬” 관련 사진 )
  • 2) random dataset ( ex. 아무 사진 )

3-2) CAVs ( Concept Activation Vectors )

[2단계] 위에서 구한 set of examples에서, 해당 concept을 나타내는 vector 찾기

• HOW? consider the activations in layer \(l\), produced by input examples that

  in the concept set vs random examples

[3단계] CAV (concept activation vector) 정의하기

• 정의) normal to a hyperplane, separating WITH/WITHOUT CONCEPT
• concept : \(C\)
  • positive set of example inputs : \(P_C\)
  • negative set : \(N\)
• binary linear classifier 학습 ( distinguish between the layer activations of two sets )
  • \(\left\{f_{l}(\boldsymbol{x}): \boldsymbol{x} \in P_{C}\right\}\).
  • \(\left\{f_{l}(\boldsymbol{x}): \boldsymbol{x} \in N\right\}\).

3-3) Directional Derivatives and Conceptual Sensitivity

Saliency map 복습 ( 위의 2-2) 참조하기 )

• use gradients of logit values w.r.t individual input features ( ex. pixel )
• 즉, 다음을 계산 : \(\frac{\partial h_{k}(\boldsymbol{x})}{\partial \boldsymbol{x}_{a, b}}\)
  • \(h_{k}(\boldsymbol{x})\) : logit for a data point \(\boldsymbol{x}\) for class \(k\)
  • \(\boldsymbol{x}_{a, b}\) : pixel at position \((a, b)\) in \(\boldsymbol{x}\).

CAV와 directional derivatives를 이용함으로써…

• sensitivity of predictions to changes in inputs towards the direction of a concept를 파악 가능!

• “Conceptual Sensitivity” :

  \(\begin{aligned} S_{C, k, l}(\boldsymbol{x}) &=\lim _{\epsilon \rightarrow 0} \frac{h_{l, k}\left(f_{l}(\boldsymbol{x})+\epsilon \boldsymbol{v}_{C}^{l}\right)-h_{l, k}\left(f_{l}(\boldsymbol{x})\right)}{\epsilon} \\ &=\nabla h_{l, k}\left(f_{l}(\boldsymbol{x})\right) \cdot \boldsymbol{v}_{C}^{l}, \end{aligned}\).

  where \(h_{l, k}: \mathbb{R}^{m} \rightarrow \mathbb{R}\).

3-4) TCAV ( Testing with CAVs )

• 위에서 CAV & directional derivatives를 통해 구한 “Conceptual Sensitivity”( = \(S_{C, k, l}(\boldsymbol{x})\) ) 사용

• notation

  • \(k\) : class label
  • \(X_k\) : class label \(k\)를 가진 모든 inputs

• TCAV score : \(\operatorname{TCAV}_{\mathrm{Q} C, k, l}=\frac{ \mid \left\{\boldsymbol{x} \in X_{k}: S_{C, k, l}(\boldsymbol{x})>0\right\} \mid }{ \mid X_{k} \mid }\).

  • the fraction of \(k\) -class inputs whose \(l\) -layer activation vector was POSITIVELY influenced by concept \(C\)

  • only depends on “sign of \(\operatorname{TCAV}_{Q, k, l}\)”
  • easily interpreted & globally

( 출처 : https://www.youtube.com/watch?v=-y0oghbEHMM&t=1127s )

3-5) Sensitivity of TCAV scores

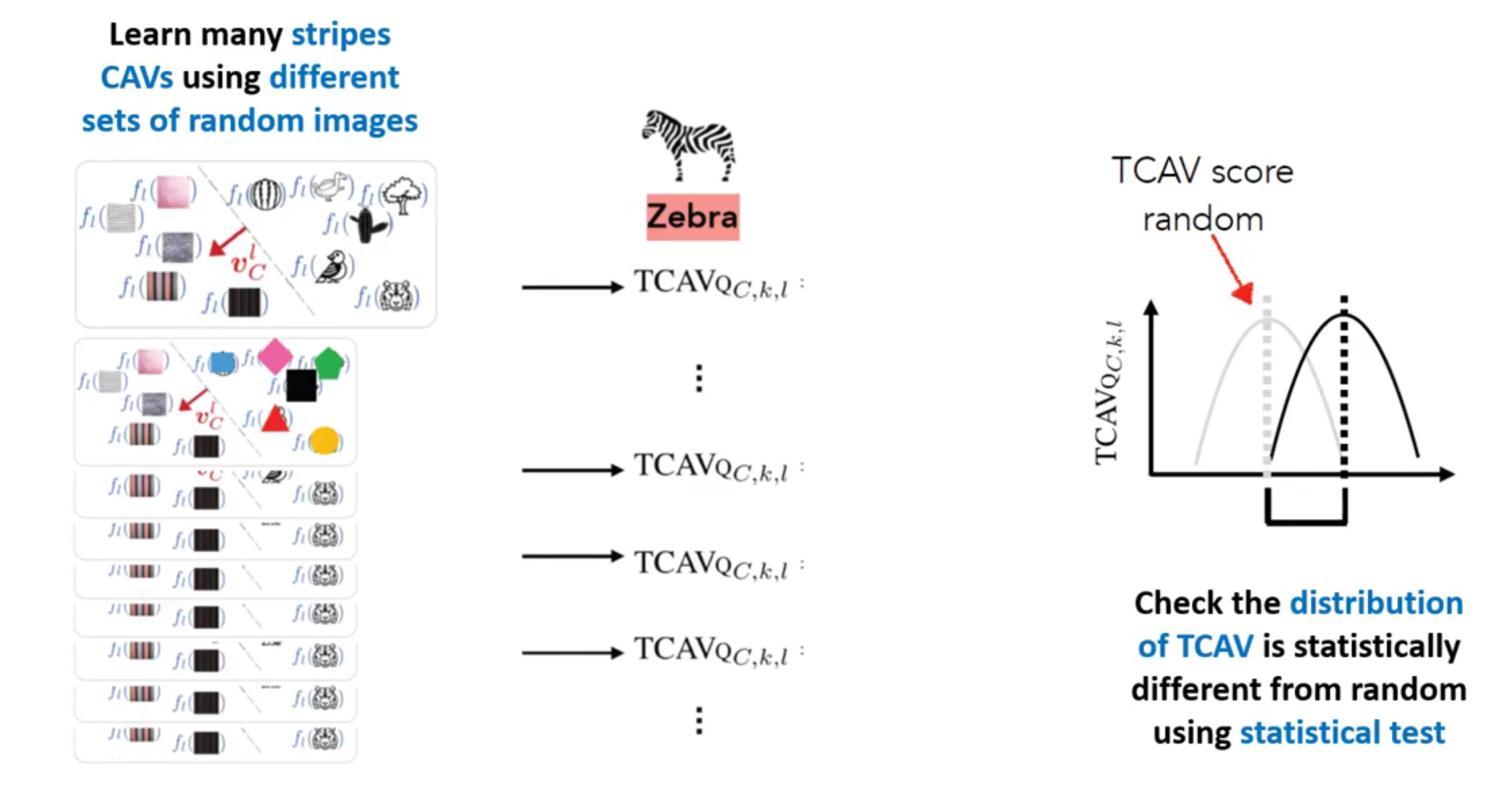
( 출처 : https://www.youtube.com/watch?v=-y0oghbEHMM&t=1127s )

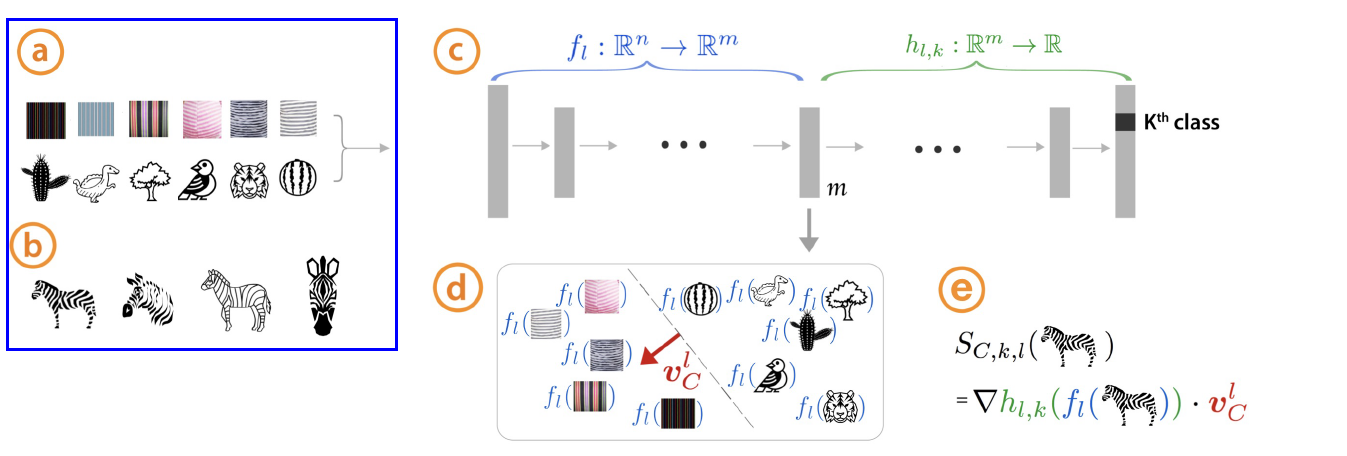
알고리즘 요약

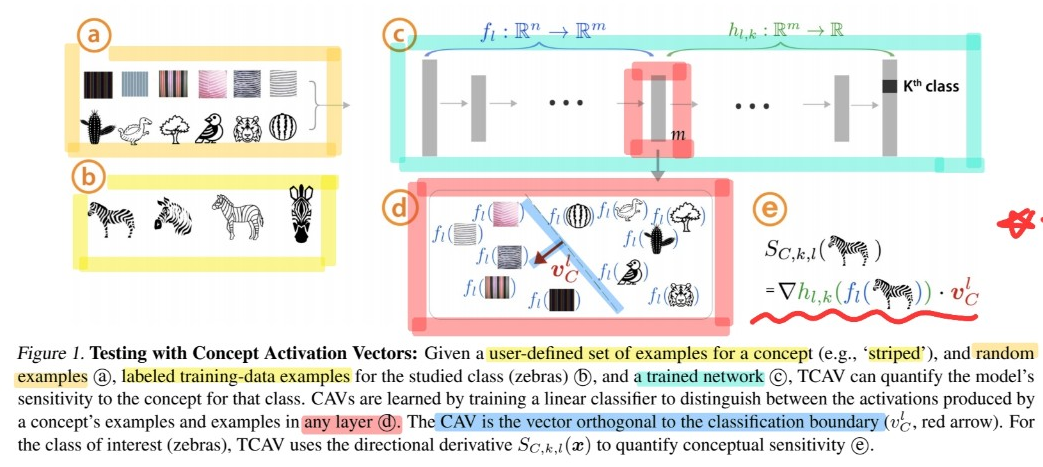
• 정의한 concept : striped (줄무늬 있는)

• (a) random examples

• (b) labeled training-data exxamples ( 줄무늬 있는 얼룩말 )

• (c) trained network

• (d) 위의 (c)에서, \(l\) 번쨰째 layer를 뽑아냄 ( 차원 : \(m\) 차원 )

  • 이를 통해 (a) & (b)를 구분하는 linear classifier
  • 여기서 hyperplane에 직교하는 선이 CAV

• (e) TCAV