Fine-Grained Abnormality Prompt Learning for Zero-shot Anomaly Detection

Fine-Grained Abnormality Prompt Learning for Zero-shot Anomaly Detection (arxiv, 2024)

Zhu, Jiawen, et al. "Fine-grained Abnormality Prompt Learning for Zero-shot Anomaly Detection." arXiv preprint arXiv:2410.10289 (2024).

참고: https://www.youtube.com/watch?v=QwEgPwCnF88

( https://arxiv.org/pdf/2410.10289 )

Contents

• (1) Overview
• (2) Background
  • Text Prompt
• (3) Methods
  • Compound abnormality prompt (CAP) learning
  • Data-dependent abnormality prompt (DAP) learning
  • Training
  • Inference

1. Overview

FAPrompt = Fine-grained Abnormality + Prompt

구성 요소

• (1) Compound Abnormality Prompting (CAP)
• (2) Data-dependent Abnormality Prompting (DAP)

CAP vs. DAP

• CAP: 다양한 종류의 abnormality prompt 구성

  \(\rightarrow\) 다양한 비정상 패턴 학습 가능

• DAP: 위를 통해 세분화된 abnormality를 통해, 다양한 데이터셋에 대해서 일반화 \(\uparrow\)

학습 과정

• CLIP의 (대부분) 원본 파라미터는 freeze
• Text Encoder의 일부 learnable token는 (ab)normality prompt에 따라 update

2. Background

(1) Text Prompt

VLM (e.g., CLIP)은 ZSAD task에서 뛰어난 모습을 보여왔음

AD task에 VLM을 적용하기 위해, 정상/비정상 textual semantic 추출이 필요!

두 종류로 나뉨

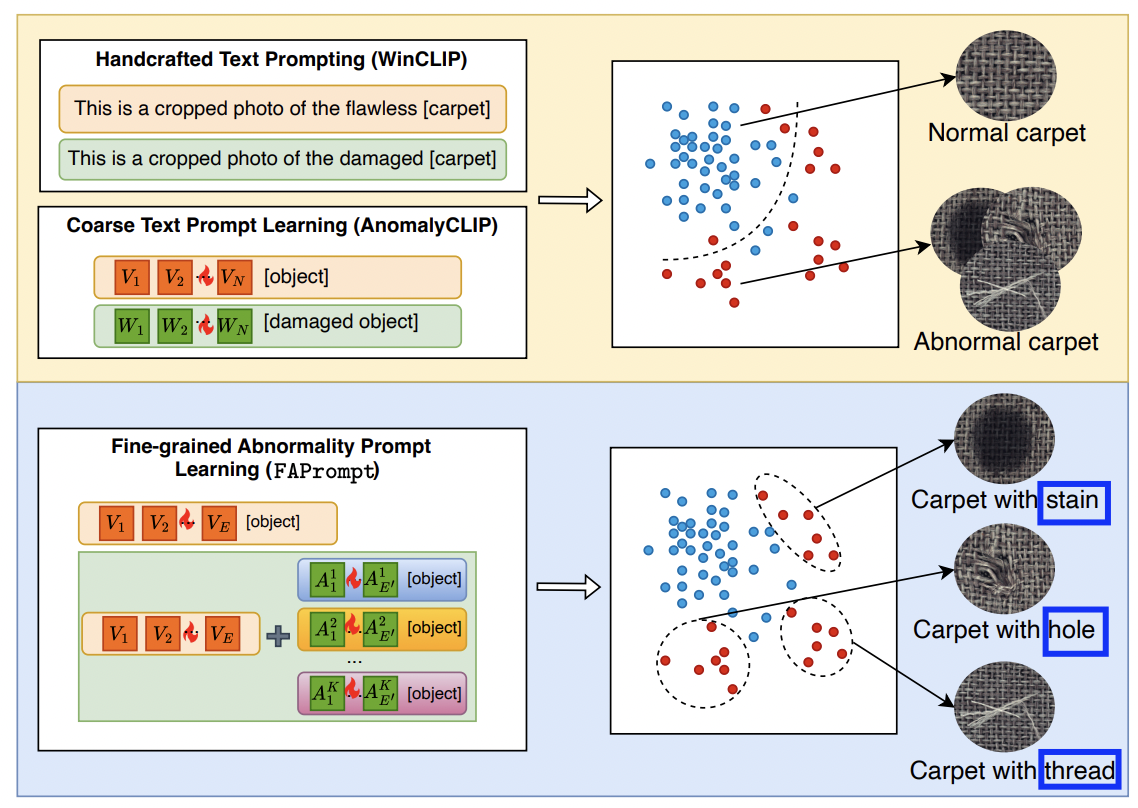
• (1) Handcrafted text prompt (e.g., WinCLIP, AnoVL)
• (2) Learnable text prompt (e.g, AnomalyCLIP)

a) Handcrafted text prompt

다양한 종류/패턴의 abnormality가 존재할 수 있음.

\(\rightarrow\) 이를 모두 커버하기 위해, “넓은 범위의 사전 학습된 token”을 text prompt에 포함시킴

Examples

• State-aware token: damaged, imperfect, defective …
• Domain-aware tokens: industrial, manufacturing, surface ..

b) Learnable text prompt

normal & abnormal class에 대한 learnable한 token

• \(g_n =\left[V_1\right]\left[V_2\right] \ldots\left[V_E\right][\text { object }]\).
• \(g_a =\left[W_1\right]\left[W_2\right] \ldots\left[W_E\right][\text { damaged }][\text { object }]\).

c) Proposed method

두 종류의 prompt를 비판함!

\(\rightarrow\) 둘 다 너무 coarse-grained semantic 에만 집중하고, fine-grained semantic을 간과한다!

( 때문에, coarse-grained abnormal pattern과는 조금 상이한 abnormal pattern는 탐지 실패할 수도!)

=> Proposal: FAPrompt

FAPrompt

Fine-grained abnormality pattern을 탐지할 수 있는 Text prompt를 학습하자!

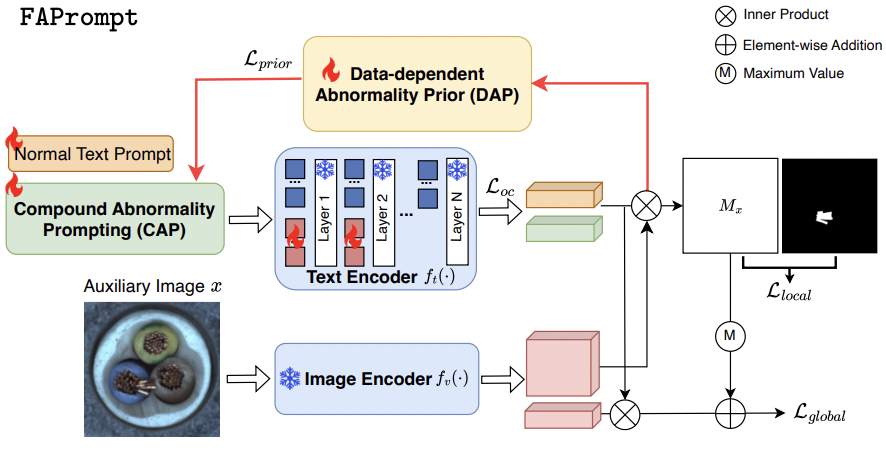
3. Methods

Overview

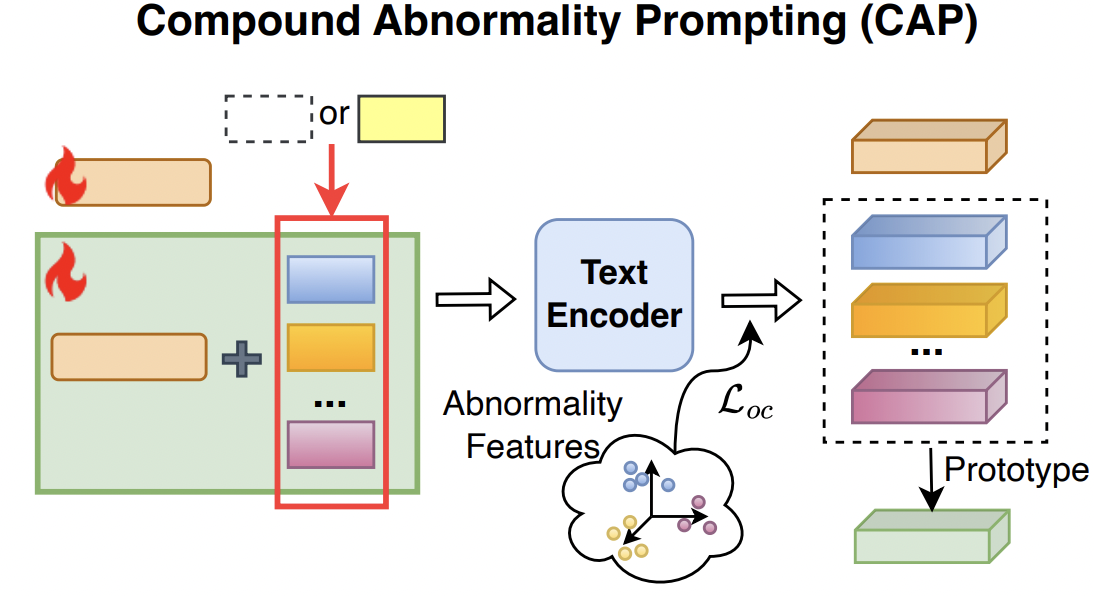
(1) Compound Abnormality Prompt Learning (CAP)

Abnormal image = 편차가 크다

• 얼룩 vs. 긁힘 vs. 색 변조 … => 너무 상이하다!

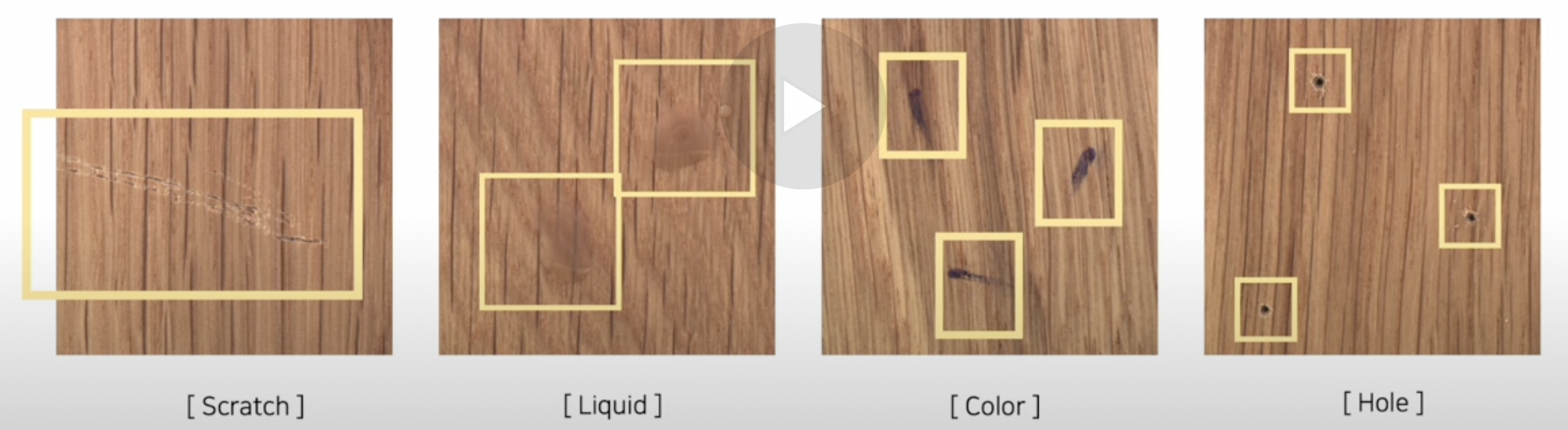
해결 방법: CAP

• “세분화된” Abnormality prompt를 사용하여, “다양한” 비정상 패턴을 학습하자

CAP의 prompt

• Normal text prompt: \(\mathcal{P}^n =\left[V_1\right]\left[V_2\right] \ldots\left[V_E\right][\text { object }]\)
• Abnormal text prompt: \(\mathcal{P}^a =\left\{\mathcal{P}^{a_1}, \mathcal{P}^{a_2}, \ldots \mathcal{P}^{a_K}\right\}\).
  • with \(\mathcal{P}^{a_i}=\left[V_1\right]\left[V_2\right] \ldots\left[V_E\right]\left[A_1^i\right]\left[A_2^i\right] \ldots\left[A_{E^{\prime}}^i\right][\text { object }]\).

• Notation

  • \(E\): normal token 개수 (default: 5)
  • \(E^{'}\): abnormal token 개수 (default: 2)
  • \(K\): fine-grained abnormal prompt 개수 (default: 10)

• 주의 사항: Abnormal text prompt 또한, (abnormal 임에도 불구하고) normal prompt를 공유한다!

  \(\rightarrow\) abnormal을 normal과 가깝게 유지시키기 위해!

Orthogonal constraint loss \(L_{oc}\)

최대한 다양한/상이한 abnormal prompt를 가지게 유도하기 위해!

• (본인을 제외한) 나머지 abnormal prompt와의 cosine similarity가 낮도록!

\(\mathcal{L}_{o c}=\sum_{i, j \in K ; i \neq j} a b s\left(\frac{f_t\left(\mathcal{P}^{a_i}\right) \cdot f_t\left(\mathcal{P}^{a_j}\right)}{\mid \mid f_t\left(\mathcal{P}^{a_i}\right)\mid \mid \times\mid \mid f_t\left(\mathcal{P}^{a_j}\right)\mid \mid }\right)\).

최종으로 사용하는 임베딩

• Normal prompt: \(F_{n}=f_t\left(P^n\right)\)

• Abnormality prompt: $$\mathbf{F}_a=\frac{1}{\left

  \mathcal{P}^a\right

  } \sum_{\mathcal{P}^{a_i} \in \mathcal{P}^a} f_t\left(\mathcal{P}^{a_i}\right)$$.

  • 전체 abnormality prompt embedding의 평균

(2) Data-dependent Abnormality Prompt Learning (DAP)

Background

ZASD에서, 모델 학습에 사용된 데이터셋 & 실제 테스트 데이터셋은 매우 상이할 수 있음!

\(\rightarrow\) Importance of generalization ability

따라서, 학습된 abnormal token의 일반화 능력을 향상시키기 위한 DAP를 제안

Idea) “가장 abnormal”한 영역의 임베딩을 선택하여, (sample-wise) abnormality prior로써 사용하자!

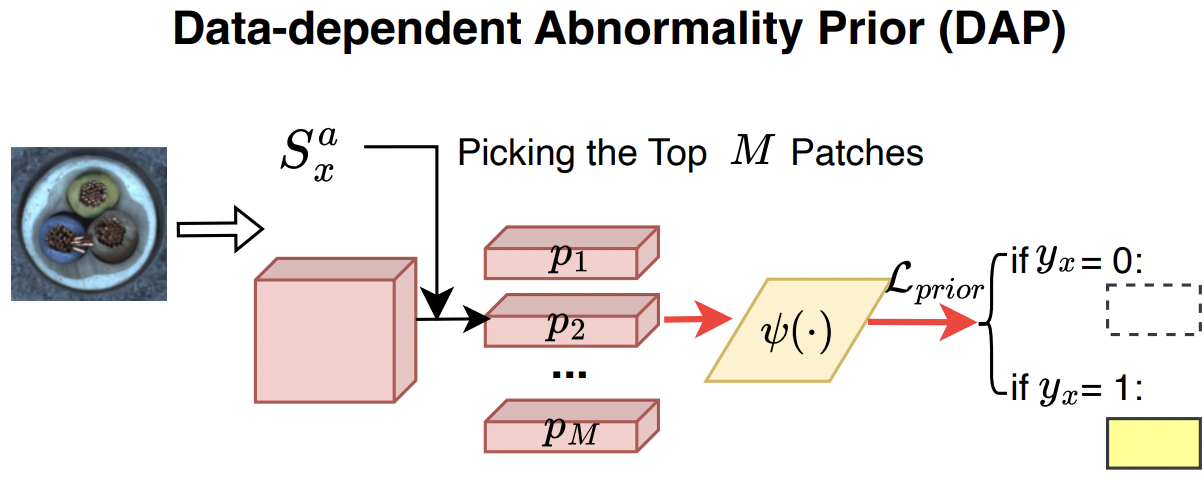
Procedure

요약: Test image \(x\)에 대해, “가장 비정상적인 image patch”를 abnormality prior로 CAP에 입력

Step 1) 이미지 내의 여러 패치들 중, 비정상 프롬프트와 가장 유사한 패치를 찾는다!

• 비정상적이다? Anomaly score로써 계산! (아래 식 참고)

• \(\mathbf{S}_x^a(i, j)=\frac{\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_a^{\top}\right)}{\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_n^{\top}\right)+\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_a^{\top}\right)}\).

  • \(M\): 패치 임베딩 개수

  • \(F_v(i,j)\): 패치 임베딩

  • \(S_x^a(i,j)\): 패치 단위의 anomaly score

Step 2) Top M개의 abnormal한 패치 임베딩을 선정한다.

Step 3) Top M개의 임베딩을 abnormality prior network에 통과시킨다.

• (1) 패치 임베딩: \(p_x=\left(p_1, p_2, \ldots, p_M\right)\)
• (2) Abnormality prior network: \(\psi(\cdot)\)

Step 4) 나온 결과값 ( = \(\psi(p_x)\))을 abnormal token에 더한다.

• \(\hat{\mathcal{P}}^{a_i}=\left[V_1\right]\left[V_2\right] \ldots\left[V_E\right]\left[A_1^i \oplus \Omega_x\right]\left[A_2^i \oplus \Omega_x\right] \ldots\left[A_{E^{\prime}}^i \oplus \Omega_x\right][\text { object }]\).

Step 5) 최종 Abnormality prompt

• (w/o DAP) \(\mathbf{F}_a=\frac{1}{\mid \mathcal{P}^a\mid } \sum_{\mathcal{P}^{a_i} \in \mathcal{P}^a} f_t\left(\mathcal{P}^{a_i}\right)\)

• (w/ DAP) $$\hat{\mathbf{F}}_a=\frac{1}{

  \hat{F} a

  } \sum_{p, p \in p^a} f_t\left(\hat{p}^{a_i}\right)$$

Abnormality prior learning loss \(L_{\text{prior}}\)

Top M개의 비정상적인 패치 정보를 더한다?

What if 정상 이미지? ( = 억지로 M개를 추가하는 것이 아닐지? )

\(\rightarrow\) 이럴 경우, prior 적용은 오히려 학습에 방해가 될 것!

Solution: abnormality prior learning loss

• \(\mathcal{L}_{\text {prior }}=\sum_{y_x=0} \sum_{\omega \in \Omega_x} \omega_x^2\).
  • \(x\)가 abnormal: \(M\)개의 패치
  • \(x\)가 normal: NULL

(3) Training

Abnormal segmentation map

• 최종 abnormality prompt: $$\hat{\mathbf{F}}_a=\frac{1}{

  \hat{F} a

  } \sum_{p, p \in p^a} f_t\left(\hat{p}^{a_i}\right)$$

• 이에 대한 anomaly map 생성 (based on 아래의 anomaly score)
  • \(\mathbf{S}_x^a(i, j)=\frac{\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_a^{\top}\right)}{\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_n^{\top}\right)+\exp \left(\mathbf{F}_v(i, j) \mathbf{F}_a^{\top}\right)}\).
  • \(\hat{\mathcal{M}}^a=\Phi\left(\hat{S}_x^a\right)\),
    • where \(\Phi\): reshape & interpolation

Normal segmentaiton map

• 위와 같은 방식으로!

a) Pixel-level AD

(AnomalyCLIP과 동일하게) Pixel-level loss 계산을 통해 optimize

\(\mathcal{L}_{\text {local }}=\frac{1}{N} \sum_{x \in X_{\text {trais }}} \mathcal{L}_{\text {Focal }}\left(\left[\hat{\mathcal{M}}^n, \hat{\mathcal{M}}^{\mathrm{a}}\right], \mathbf{G}_x\right)+\mathcal{L}_{\text {Dice }}\left(\hat{\mathcal{M}}^a, \mathbf{G}_x\right)+\mathcal{L}_{\text {Dice }}\left(\dot{\mathcal{M}}^{\mathrm{n}}, \mathbf{I}-\mathbf{G}_x\right)\).

• \(\mathbf{G}_x\): ground-truth mask
• \(\mathbf{I}\) : one matrix

b) Image-level AD

• Test image \(x\) & normal/abnormal prompt embedding간의 유사도 계산
  • \(s_a(x)=\frac{\exp \left(f_v(x) \hat{\mathbf{F}}_a^{\top}\right)}{\exp \left(f_v(x) \mathbf{F}_n^{\top}\right)+\exp \left(f_v(x) \hat{\mathbf{F}}_a^{\top}\right)}\).

최종 Image-level anomaly score:

= image-level score & pixel-score의 최대값 간의 평균값

• \(s(x)=\frac{1}{2}\left(s_a(x)+s_a^{\prime}(x)\right)\).
  • where \(s_a^{\prime}(x)=\frac{1}{2}\left(\max \left(S_x^a\right)+\max \left(\hat{S}_x^a\right)\right)\).

Image-level loss

\(\mathcal{L}_{\text {global }}=\frac{1}{N} \sum_{x \in X_{\text {train }}} \mathcal{L}_b\left(s(x), y_x\right)\).

• \(\mathcal{L}_b\): focal loss ( due to imbalance in train dataset )

c) 전체 Loss

\(\mathcal{L}=\mathcal{L}_{\text {local }}+\mathcal{L}_{\text {global }}+\mathcal{L}_{\text {prior }}+\mathcal{L}_{o c}\).

(4) Inference

Test image \(x^{'}\)이 주어지면, CLIP의 visual encoder를 통과하여, 4종류의 segmentation map을 생성함..

그런 뒤, pixel-level anomaly map을 아래와 같이 계산함!

• \(\mathcal{M}_{x^{\prime}}=\frac{1}{4}\left(\mathcal{M}^a \oplus 1 \ominus \mathcal{M}^n \oplus \hat{\mathcal{M}}^a \oplus 1 \ominus \hat{\mathcal{M}}^n\right)\).

( image-level anomaly score는, 앞서 언급한 것 처럼 )

• \(s(x)=\frac{1}{2}\left(s_a(x)+s_a^{\prime}(x)\right)\).