HydraLoRA; An Asymmetric LoRA Architecture for Efficient Fine-Tuning (NeurIPS 2024)Permalink

Tian, Chunlin, et al. "HydraLoRA: An Asymmetric LoRA Architecture for Efficient Fine-Tuning." NeurIPS (2024)

( https://arxiv.org/pdf/2404.19245 )

ContentsPermalink

• (1) Abstract
• (2) Limitation of LoRA
• (3) HydraLoRA
  • LoRA
  • HydraLoRA
• (4) Workflow of HydraLoRA
  • Fine-tuning
  • Inference

1. AbstractPermalink

(1) LoRA: Widely used Parameter-Efficient Fine-Tuning (PEFT) technique

(2) Limitation of LoRA: Often underperform compared to full fine-tuning

• ( especially in complex datasets )

(3) Proposal: HydraLoRA

• LoRA framework with an asymmetric structure that eliminates the need for domain expertise

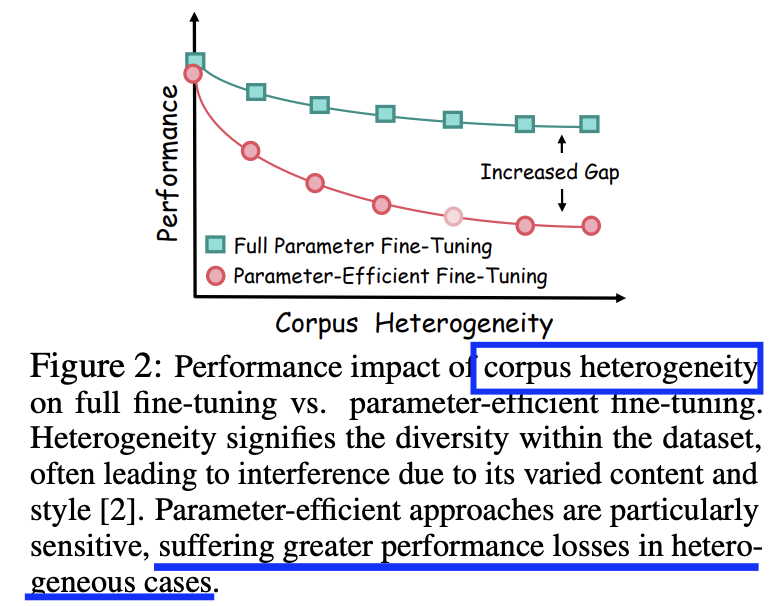
2. Limitation of LoRAPermalink

Underperform compared to full fine-tuning, especially in heterogeneous datasets

3. HydraLoRAPermalink

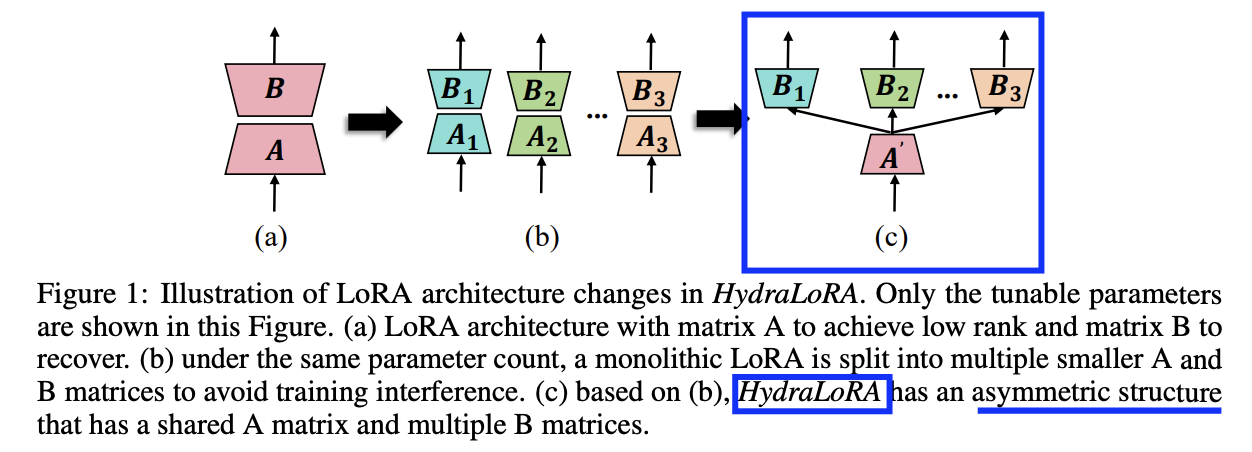
(1) LoRAPermalink

$y \prime=y+\Delta y=W_0 x+B A x$,

• $y \in R^{\mathrm{d}}$: output

• $x \in R^{\mathrm{k}}$: input

• $B \in R^{\mathrm{d \times r}}, A \in R^{\mathrm{r \times k}}$ with $r \ll \min (d, k)$.

  • $B$ is initialized with zeroes

  • $A$ is initialized with Kaiming Uniform [14]

    $\rightarrow$ to force $\Delta y=0$ at the beginning

(2) HydraLoRAPermalink

$\begin{aligned} W & =W_0+\Delta W \\ & =W_0+\sum_{i=1}^N \omega_i \cdot B_i A \end{aligned}$.

• $B_i \in \mathbb{R}^{d \times r}$ $\rightarrow$ $N$ matrices
• $A \in \mathbb{R}^{r \times k}$. $\rightarrow$ single matrix (shared)
• $\omega_i$: modulates these contribution weights for head $B_i$

4. Workflow of HydraLoRAPermalink

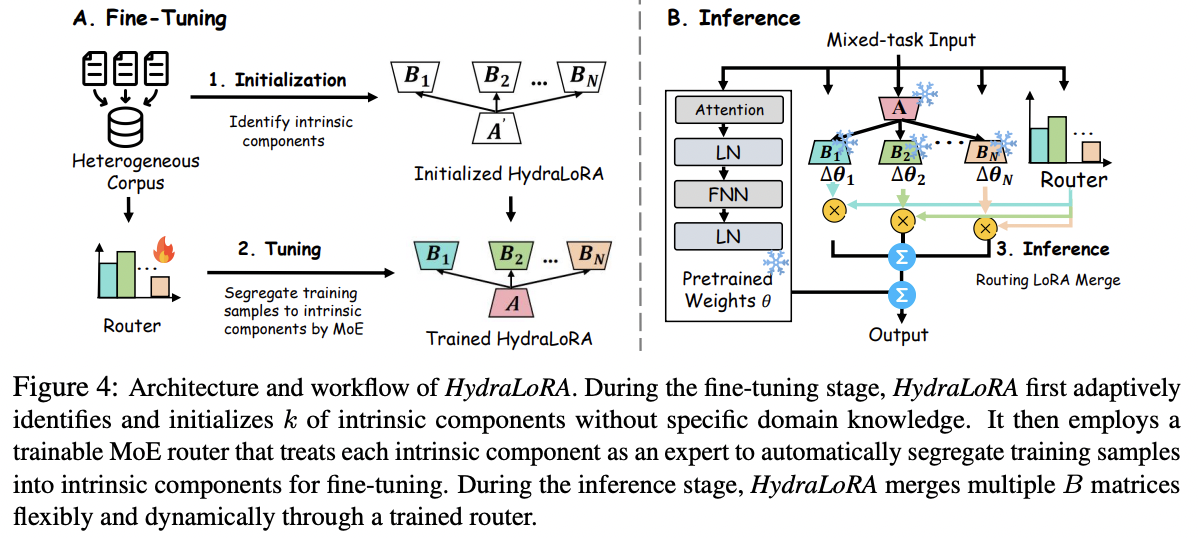
(1) Fine-tuningPermalink

MoE (Mixture-of-Experts) = Experts are selectvely activated by a gating mechanism (router)

a) Set of expertsPermalink

To achieve a unified approach of multiple $B$ matrices…

$\rightarrow$ Define a set of experts: $\left(E_1, \ldots, E_N\right)$

Interpretation

• (1) Shared matrix $A$ : inherently captures collaborative knowledge to augment intra-gains
• (2) Different matrices $B$ : foster knowledge modularity to mitigate fine-tuning inter-offsets

b) RouterPermalink

$\omega_i=\operatorname{softmax}\left(W_g^T x\right)$.

• trainable weights (transformation matrix) $W_g \in \mathbb{R}^{r \times N}$

$\rightarrow$ becomes a gating scores $\left(\omega_1, \ldots, \omega_N\right)$

c) HydraLoRAPermalink

$y=W_0 x+\sum_{i=1}^N \omega_i E_i A x \quad(M o E)$.

• where $N$ denotes the number of experts, i.e., $B$ matrices.

(2) InferencePermalink

Merges adapters by enabling routing computation based on the input!