Mixture-of-Experts with Expert Choice Routing

Mixture-of-Experts with Expert Choice Routing (NeurIPS 2022)

Zhou, Yanqi, et al. "Mixture-of-experts with expert choice routing." Advances in Neural Information Processing Systems 35 (2022): 7103-7114.

( https://arxiv.org/pdf/2202.09368 )

참고:

• https://www.youtube.com/watch?v=JyGfOlKzVqk
• https://cameronrwolfe.substack.com/p/conditional-computation-the-birth

Contents

• Overview
• (1) MoE
• (2) MoE Layer
• (3) Token-choice routing의 한계점
• (4) Proposed: Expert Choice

Overview

Mixture-of-Experts

• Layer 내부의 network를 input에 대해 부분적으로 activate

\(\rightarrow\) compuation cost 대비 많은 수의 parameter 증가 가능

( \(\because\) gating mechanism을 통한 sparse activation 덕분! 데이터당 소수의 expert만 활용하게 하여, 효율적인 계산이 가능해짐 )

MoE vs. Proposed

• MoE: “data(token)”를 expert에 핼당
• Proposed: “expert”를 data(token)에 핼당

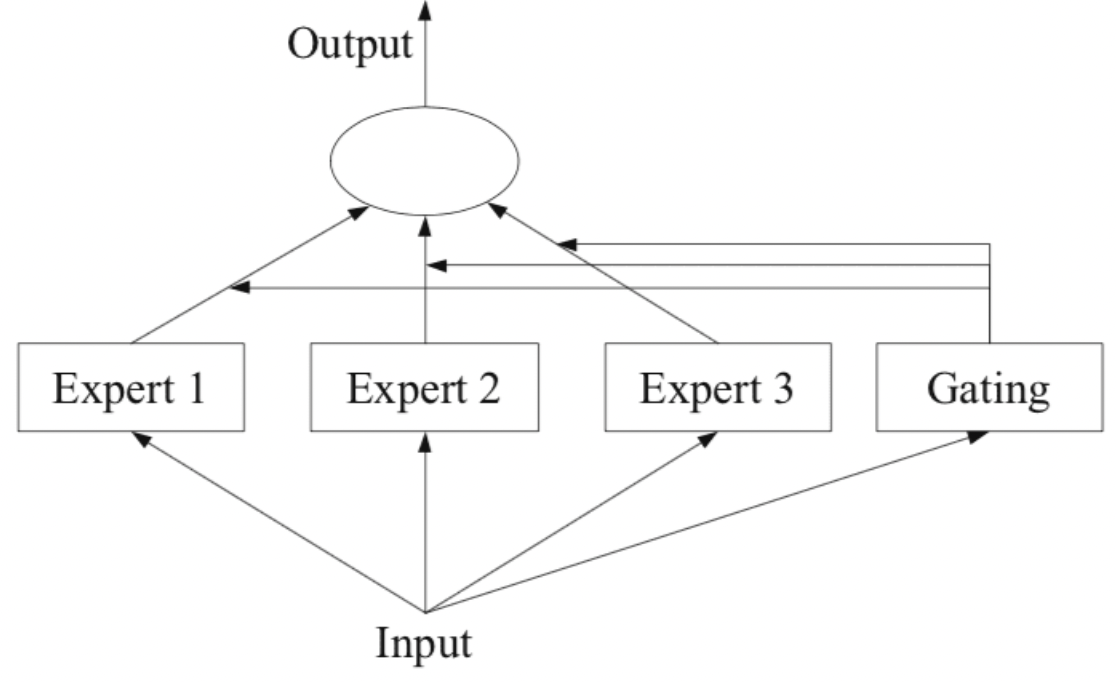
1. MoE

Model = (1) Expert network + (2) Gating Network

• (1) Expert network: target task를 푸는 모델
• (2) Gating network: input을 어떠한 expert에 할당할지 결정하는 모델 (i.e., Router)

\(\rightarrow\) Key point: 각 expert가 서로 다른 subtask에 대해 specialize하도록!

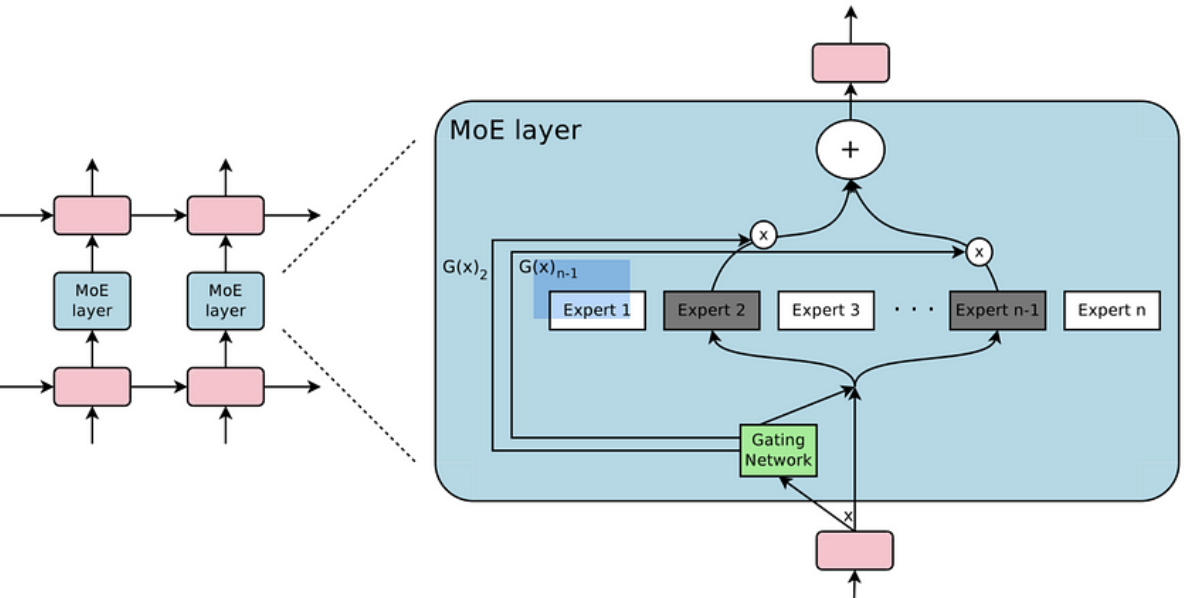
\(y=\sum_{i=1}^n G(x)_i \cdot E_i(x)\).

• \(G(x)\): Router output
• \(E_i(x)\): Expert output
• \(y\): MoE output

2. MoE Layer

a) Conditional computation

• 데이터에 따라 network의 일부분을 활성화/비활성화

\(\rightarrow\) (parameter 수 증가 대비) computational cost 증가량 감소

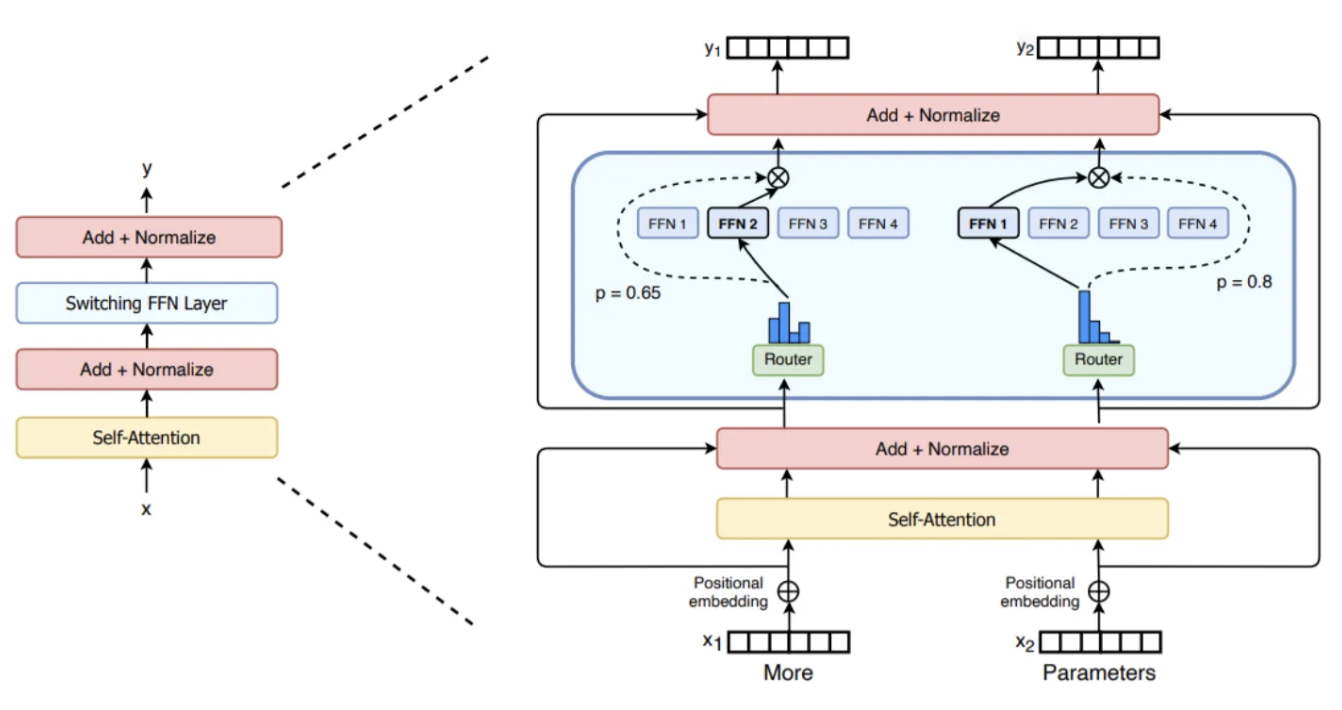
b) Sparsely gated MOE layer

• MoE in deep learning
• Each expert = FFN
• Stacked LSTM 층 사이에 MOE layer 삽입

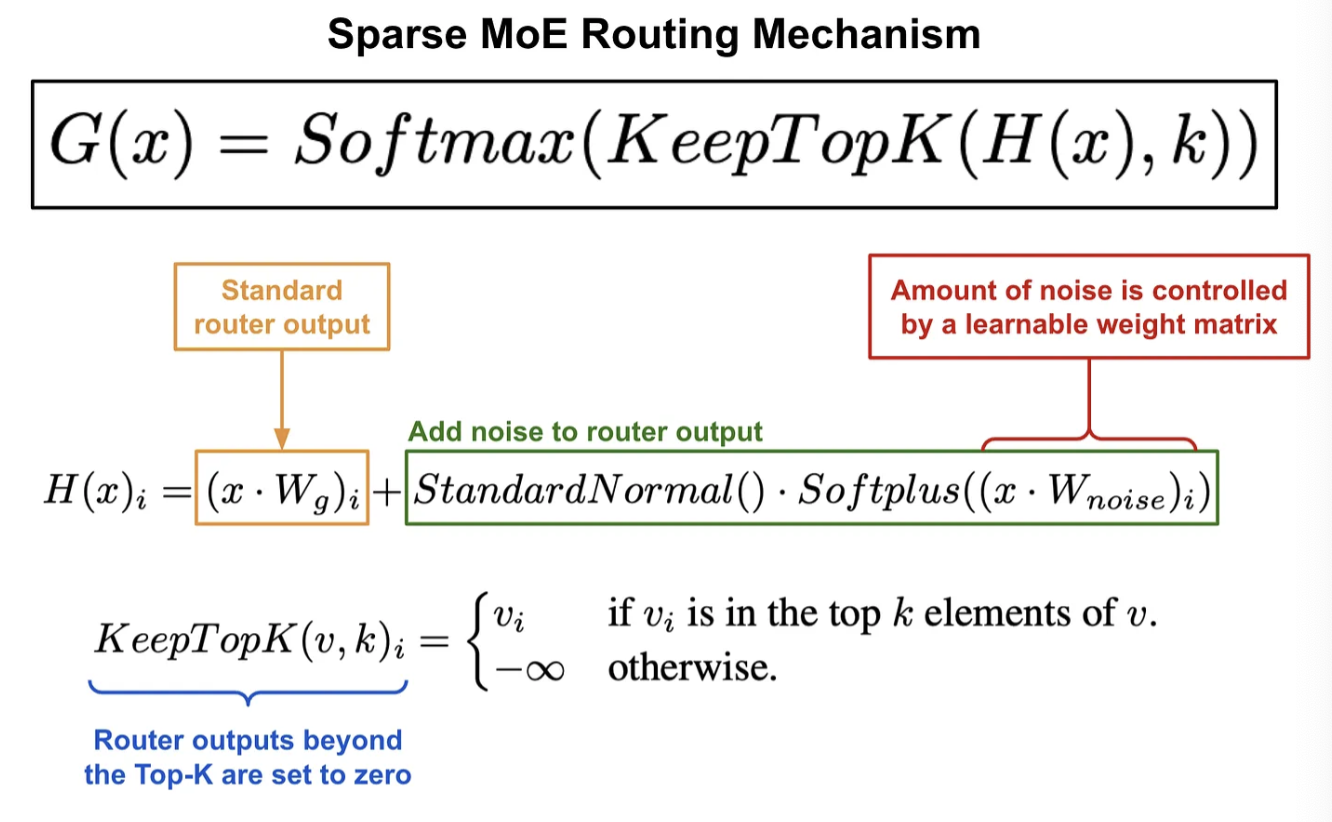
c) Balancing Expert utilization

문제점: 특정 expert에 모든 데이터가 할당되어버린다면…?

\(\rightarrow\) Regularization을 활용한 soft constraint approach 사용!

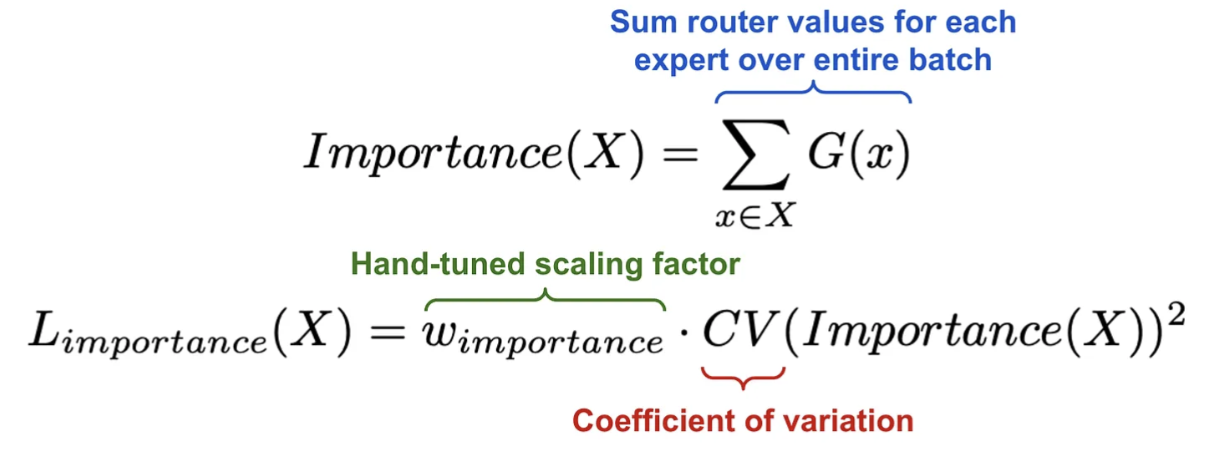
• (1) Expert 별로 importance(X)를 구함
• (2) 이들이 서로 고르게 되도록 유도하는 loss term

3. Token-choice routing의 한계점

한계점 3가지

• (1) Load imbalance
• (2) Under specialization
• (3) Same compute for every token

(1) Load imbalance

• 특정 expert에 대부분의 data가 몰리는 현상

  (e.g., 일부 expert에 ~40%의 over-capacity ratio)

• 결과: 많은 데이터(token)이 drop됨

(2) Under specialization

• Reg loss를 통해, 억지로 적절하지 않은 expert에 할당되게 될 수도!
• 즉, loss는 최적화될지언정, under specialization 발생!

(3) Same compute for every token

• 기존의 routing strategy: 각 데이터에 모두 같은 수의 expert가 할당됨

\(\rightarrow\) 데이터의 complexity에 따라 서로 다른 computation을 가지는게 더 plausible!

4. Proposed: Expert Choice

역으로, Expert를 data에 할당하자!

• (Before) 데이터 당 Top K개의 expert를 할당

• (After) expert 당 Top K개의 데이터를 할당

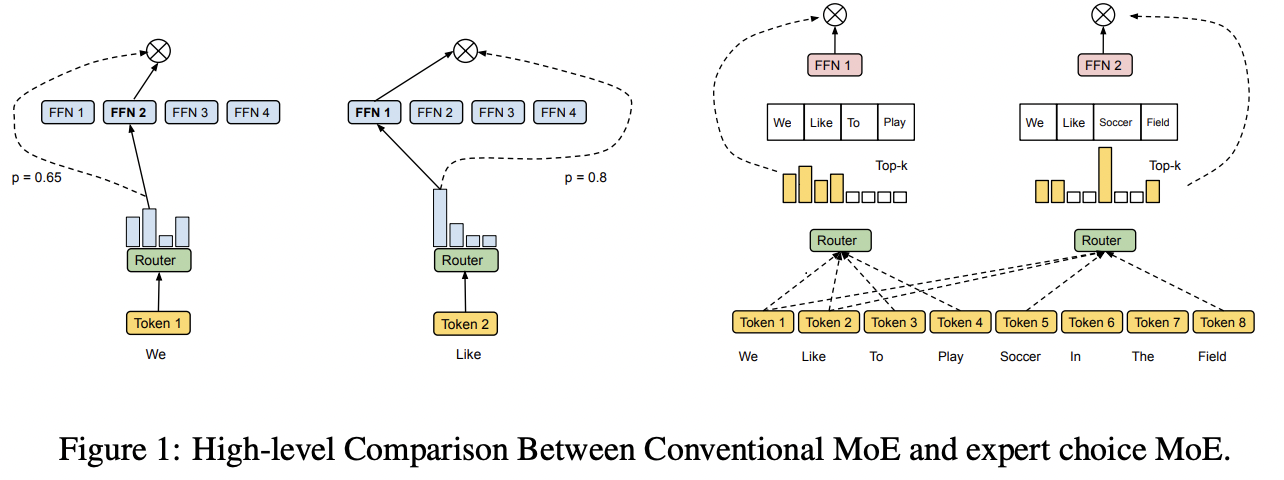
Notation

(Top \(k\)) \(k=\frac{n \times c}{e}\)

• (1) \(n\): # of data(tokens) in input batch

  • (batch size \(\times\) sequence length)

• (2) \(c\): capacity factor

  • How many experts are utilized by a token

    ( Higher \(c\) \(\rightarrow\) More tokens are assigned! )

• (3) \(e\): # of experts

Input token representations: \(X \in \mathbb{R}^{n \times d}\)

• where \(d\) is the hidden dimension

Token-to-expert assignment: \(I, G\) and \(P\).

• \(I\) : Index matrix
  • \(I[i, j]\) : \(j\)-th selected token of the \(i\)-th expert.
• \(G \in \mathbb{R}^{e \times k}\): Gating matrix
  • Weight of expert for the selected token
• \(P \in \mathbb{R}^{e \times k \times n}\): One-hot version of \(I\)
  • Will be used to gather tokens for each expert.

Procedure

Step 1) Token-to-expert affinity scores

• 데이터 & Expert 사이의 유사도
• \(S=\operatorname{Softmax}\left(X \cdot W_g\right)\), where \(S \in \mathbb{R}^{n \times e}\)

Step 2) Gating matrix & one-hot matrix

• \(G, I=\operatorname{TopK}\left(S^{\top}, k\right)\), where \(P=\operatorname{Onehot}(I)\)

Step 3) Output of each expert

• \(X_e[i]=\operatorname{GeLU}\left(X_{i n}[i] \cdot W_1[i]\right) \cdot W_2[i]^{\top}\), where \(X_{\text {in }}=P \cdot X\).

Step 4) Total output

• \(X_{\text {out }}[l, d]=\sum_{i, j} P[i, j, l] G[i, j] X_e[i, j, d]\),