From Sparse to Soft Mixture of Experts (Soft MoE)

From Sparse to Soft Mixture of Experts (ICLR 2024)

Puigcerver, Joan, et al. "From sparse to soft mixtures of experts." ICLR 2024

( https://arxiv.org/abs/2308.00951 )

참고:

• https://aipapersacademy.com/from-sparse-to-soft-mixture-of-experts/

Contents

1. Background
2. Sparse vs. Soft MoE
3. Sparse MoE
4. Soft MoE
   1. Architecture
   2. Notation
   3. Details

1. Background

Trend: 점점 더 커지는 모델

\(\rightarrow\) 높아지는 computational cost

\(\rightarrow\) Mixure of Experts (MoE)의 등장! (used by GPT-4)

2. Sparse vs. Soft MoE

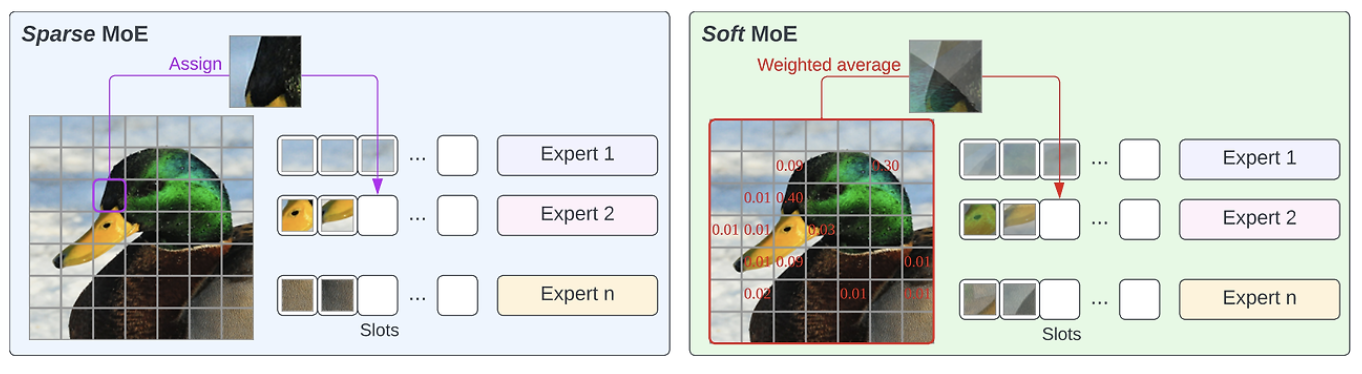
3. Sparse MoE

데이터를 적절한 expert에 할당(hard, sparse, discrete)해서 풀자!

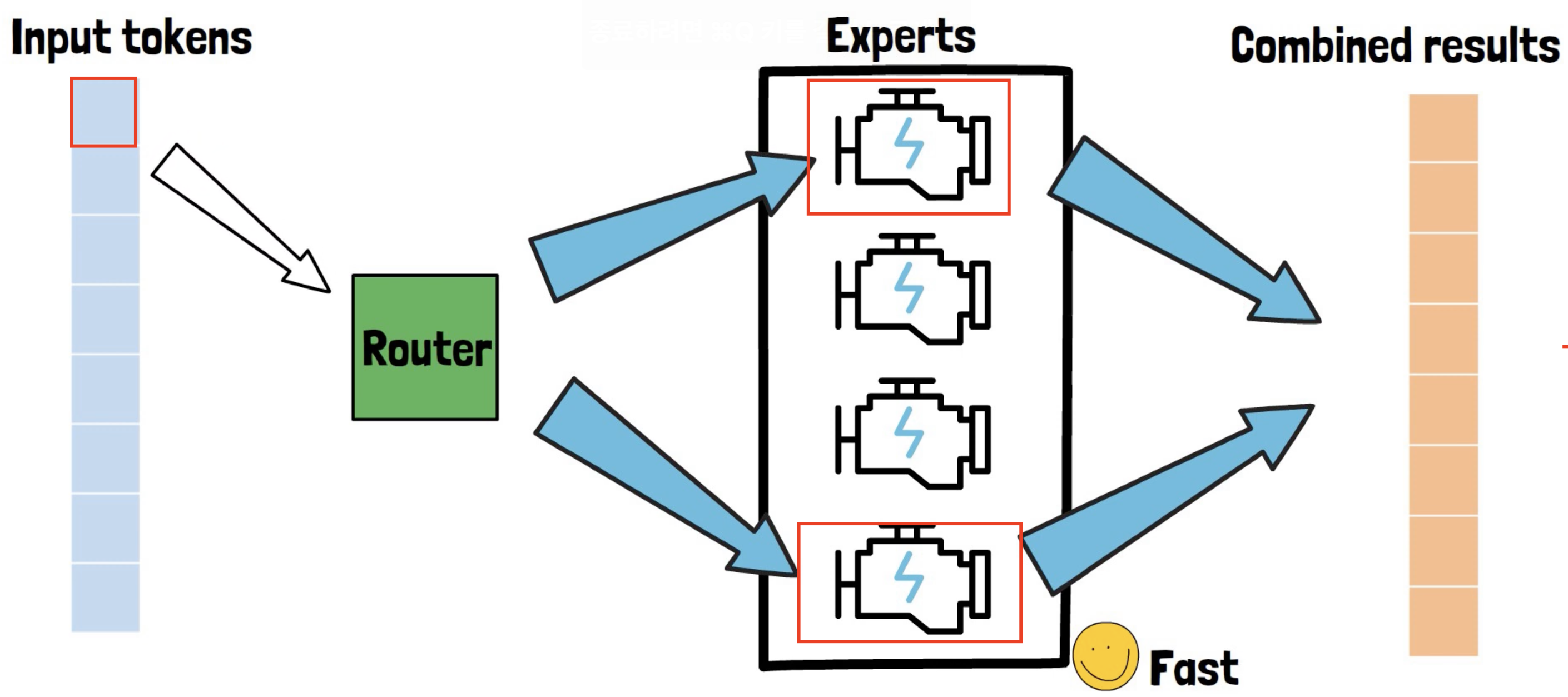
Router의 역할 = token을 적절한 expert에 할당해줌

Sparse MoE의 Issue?

• Discrete optimization
• Hard to scale the # of experts

3. Soft MoE

Goal = MoE의 한계점을 극복

핵심

• 기존) 하나의 token \(\rightarrow\) K개의 expert에 할당
• 제안) 모든 token의 combination \(\rightarrow\) 모든 expert에 할당

(1) Architecture

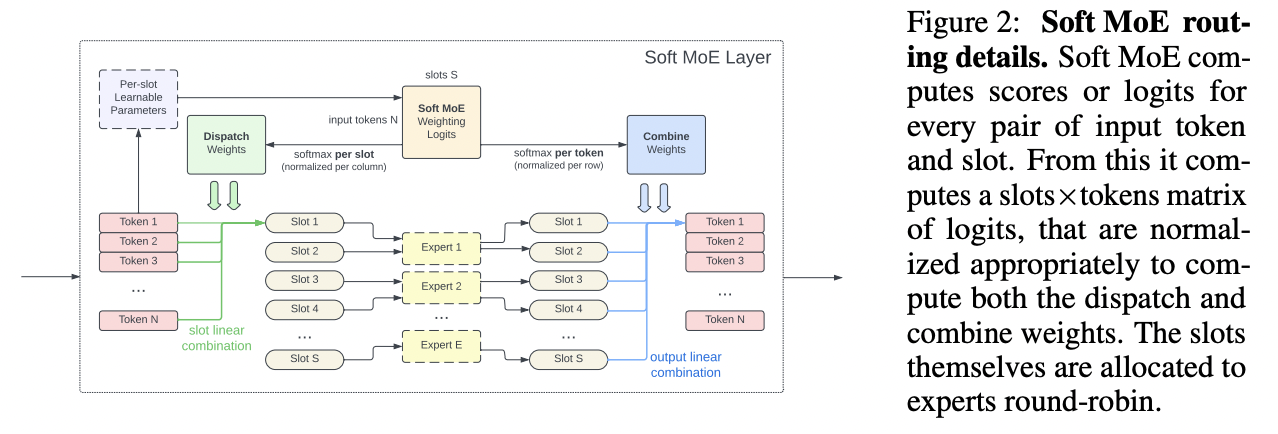
(2) Notation

• Input token: \(\mathbf{X} \in \mathbb{R}^{m \times d}\)
  • \(m\): token의 개수
  • \(d\): dimension
• \(n\)개의 expert
  • \(\left\{f_i: \mathbb{R}^d \rightarrow \mathbb{R}^d\right\}_{1=n}\).

(3) Details

Expert는 (token)대신 slot을 process한다

• 각 expert는 \(p\)개의 slot을 처리함 (\(\Phi \in \mathbb{R}^{d \times(n \cdot p)}\))

[Step 1] Input slots: \(\tilde{\mathbf{X}} \in \mathbb{R}^{(n\cdot p) \times d}\)

• Convex combinations of all the \(m\) input tokens

• \(\tilde{\mathbf{X}}=\mathbf{D}^{\top} \mathbf{X} \in \mathbb{R}^{n\cdot p \times d}\).

  • Dispatch weights = \(\mathbf{D} \in \mathbb{R}^{m\times n\cdot p}\): token & slot과의 관계

  • where \(\mathbf{D}_{i j}=\frac{\exp \left((\mathbf{X} \boldsymbol{\Phi})_{i j}\right)}{\sum_{i^{\prime}=1}^m \exp \left((\mathbf{X} \boldsymbol{\Phi})_{i^{\prime} j}\right)}\)

    ( = Softmax over the columns of \(\mathbf{X} \Phi\). )

[Step 2] Expert가 slot을 처리함 (on rows of \(\tilde{\mathbf{X}})\)

• Output slots: \(\tilde{\mathbf{Y}}_i=f_{\lfloor i / p]}\left(\tilde{\mathbf{X}}_i\right)\).

[Step 3] Output에 대해 linear combination (\(\mathbf{Y}=\mathbf{C} \tilde{\mathbf{Y}}\))

• Convex combination of all ( \(n \cdot p\) ) output slots

• \(\mathbf{C}_{i j}=\frac{\exp \left((\mathbf{X} \Phi)_{i j}\right)}{\sum_{j^{\prime}=1}^{n-p} \exp \left((\mathbf{X} \Phi)_{i j^{\prime}}\right)}\).

  • Combine weights = \(\mathbf{D} \in \mathbb{R}^{m\times n\cdot p}\)

    ( = Softmax over the rows of \(\mathbf{X} \Phi\). )

기타

• (Sparse MoEs와 마찬가지로) Transformer’s MLP blocks를 Soft MoE blocks로 대체함
  • Typically replace the second half of MLP blocks
• # slot = key hyperparameter of Soft MoE layers
  • \(\because\) Time complexity가 (# expert보다) # slot에 의존함