VQ-VAE

VQ-VAE

Van Den Oord, Aaron, and Oriol Vinyals. "Neural discrete representation learning." Advances in neural information processing systems 30 (2017).

Contents

1. Introduction
2. VQ-VAE
   1. Discrete Latent Variable
   2. Learning
   3. Prior
3. Experiments

1. Abstract

VQ-VAE

Vector Quantised VAE

• Simple yet powerful generative model that learns discrete representations

• Differs from VAEs in two key ways:

  • (1) Encoder: Outputs discrete codes
  • (2) Prior: Learnt rather than static

• Key idea: vector quantisation (VQ)

  \(\rightarrow\) Allows the model to circumvent issues of “posterior collapse”

  ( where the latents are ignored when they are paired with a powerful autoregressive decoder )

2. VQ-VAE

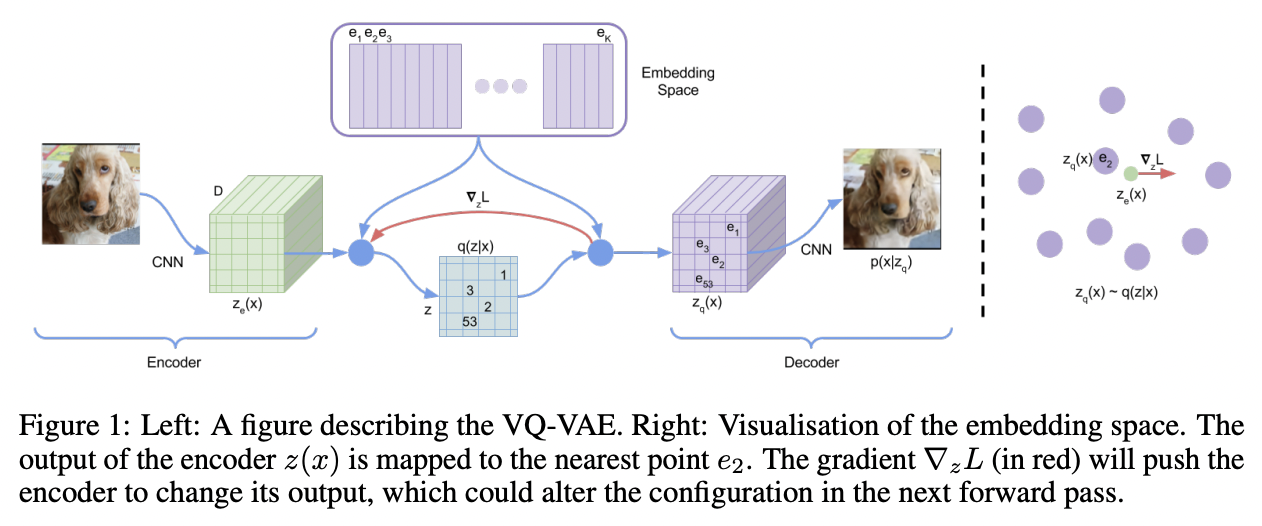
(1) Discrete Latent Variables

Latent embedding space \(e \in R^{K \times D}\)

• \(K\) : Size of the discrete latent space (i.e., a \(K\)-way categorical)
• \(D\) : Dimensionality of each latent embedding vector \(e_i\).

\(\rightarrow\) There are \(K\) embedding vectors \(e_i \in R^D, i \in 1,2, \ldots, K\).

Procedure

• Step 1) Takes an input \(x\)
• Step 2) Encoding
  • Produce output \(z_e(x)\).
• Step 3) Find the nearest neighbor
  • \(z\) are then calculated by a NN look-up using the shared embedding space \(e\)
  • \(q(z=k \mid x)= \begin{cases}1 & \text { for } \mathrm{k}=\operatorname{argmin}_j \mid \mid z_e(x)-e_j \mid \mid _2 \\ 0 & \text { otherwise }\end{cases}\).
• Step 4) Decoding
  • Input to the decoder: NN
    • \(z_q(x)=e_k, \quad \text { where } \quad k=\operatorname{argmin}_j \mid \mid z_e(x)-e_j \mid \mid _2\)…. Eq (2)

(2) Learning

No real gradient defined for Eq (2)

\(\rightarrow\) Solve with detach (stop gradient)

Loss function:

• \(L=\log p\left(x \mid z_q(x)\right)+ \mid \mid \operatorname{sg}\left[z_e(x)\right]-e \mid \mid _2^2+\beta \mid \mid z_e(x)-\operatorname{sg}[e] \mid \mid _2^2\).

Log-likelihood of the model \(\log p(x)\):

• \(\log p(x)=\log \sum_k p\left(x \mid z_k\right) p\left(z_k\right)\).

(3) Prior

Prior distribution over the discrete latents \(p(z)\) : Categorical distribution

Whilst training the VQ-VAE

\(\rightarrow\)the prior is kept constant and uniform

After training,

\(\rightarrow\) Fit an autoregressive distribution over \(z, p(z)\), so that we can generate \(x\) via ancestral sampling

3. Experiments