The Era of 1-bit LLMs; All Large Language Models are in 1.58 Bits

The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits

Ma, Shuming, et al. "The era of 1-bit llms: All large language models are in 1.58 bits." arXiv preprint arXiv:2402.17764 (2024).

참고:

• https://aipapersacademy.com/the-era-of-1-bit-llms/
• https://arxiv.org/abs/2402.17764

Contents

1. Post-training Quantization
2. Abstract of BitNet b1.58
3. Benefits of BitNet b1.58
   1. Additions Instead Of Multiplications
   2. Feature Filtering
   3. Reduce Cost Without Performance Penalty
4. Model Architecture
5. Experiments

1. Post-training Quantization

LLM is getting larger and larger!

\(\rightarrow\) How to efficiently run LLMs?

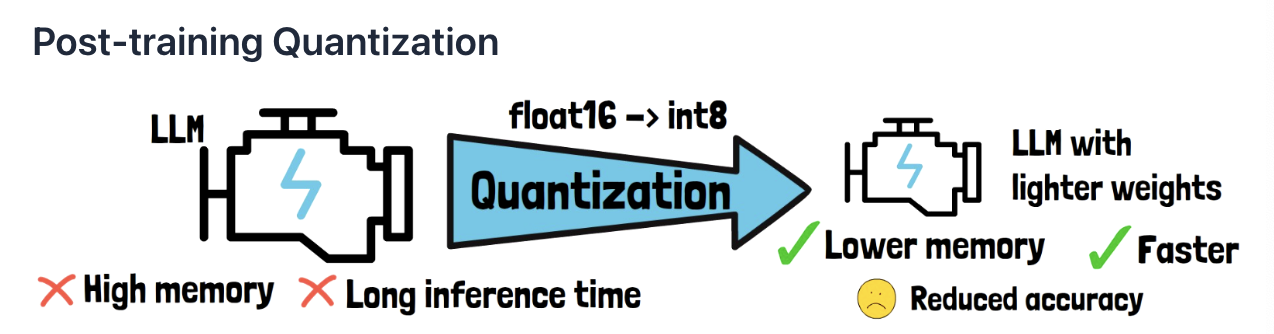
Quantization

• Process of reducing the precision of the model weights

• e.g., Converting the model weights from float16 to int8

  \(\rightarrow\) So each weight is one byte in memory instead of four

• Limitation: Decrease in the model accuracy

2. Abstract of BitNet b1.58

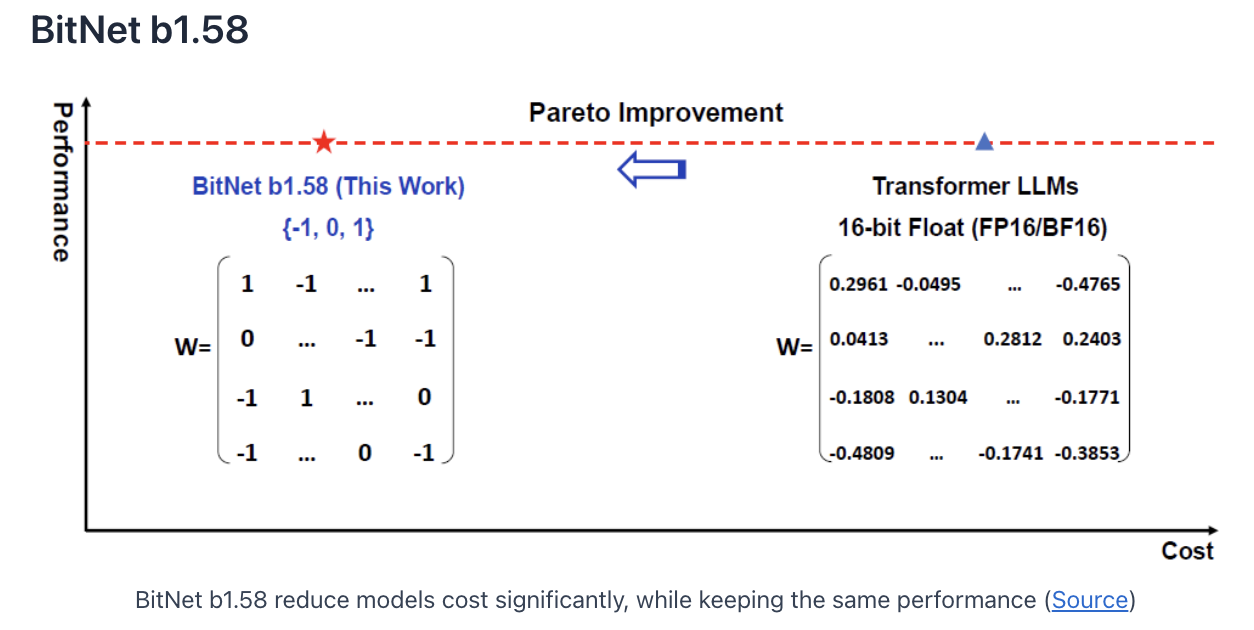
Propose BitNet b1.58

Three key points

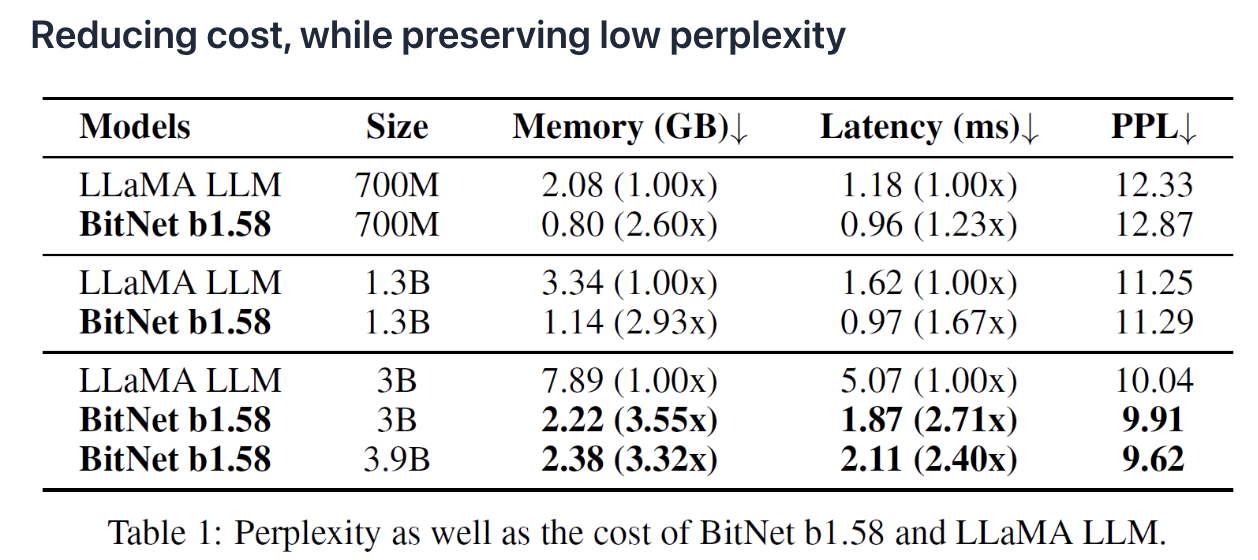
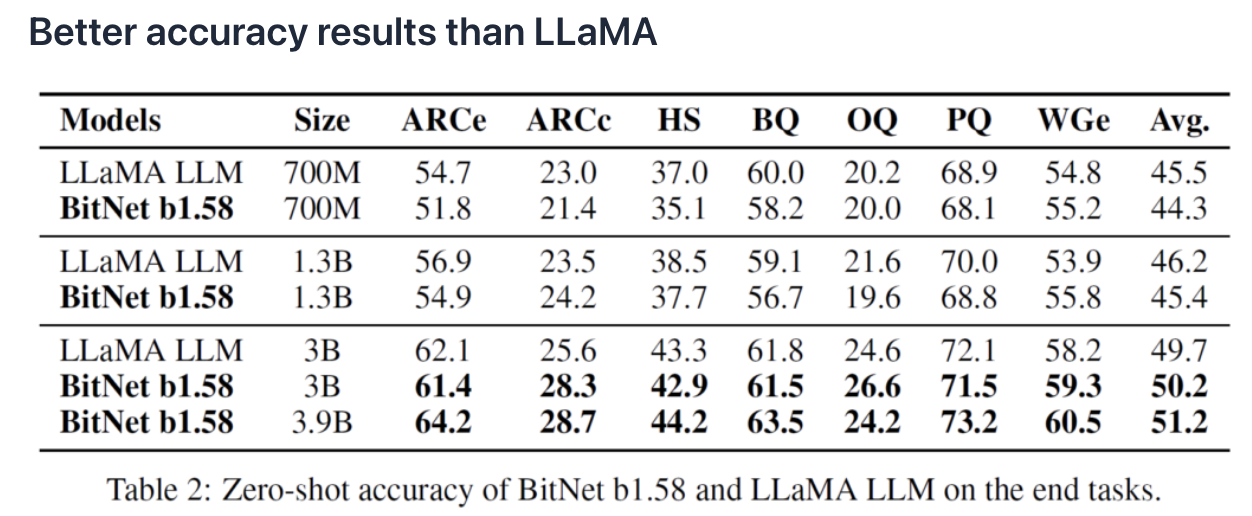
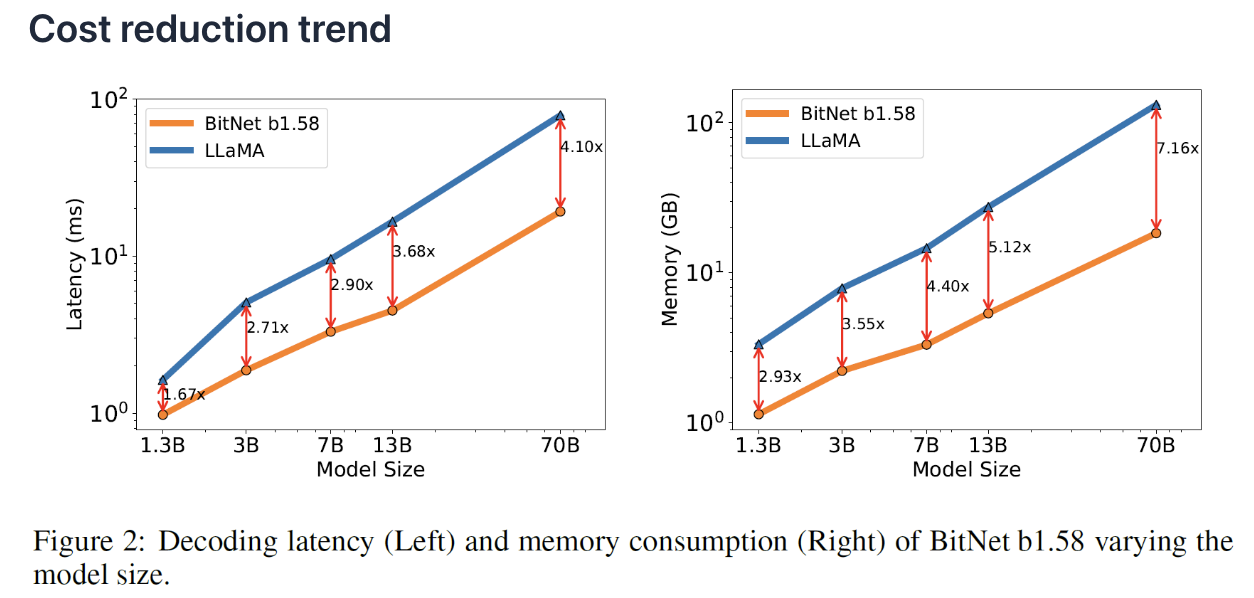
• (1)Reduce cost, while maintaining performance

• (2) Ternary weights

  • Every weight is either -1, 0 or 1

    \(\rightarrow\) Need less than 16 bits to represent the three possible values!

  • How many bits are required? \(\log_2(3) \approx 1.58\)

    \(\rightarrow\) model weights are a bit more than 1 bit!!

• (3) Trained from scratch

  • NOT adapted after the training

    \(\rightarrow\) The model learns during training how to work with ternary weights

3. Benefits of BitNet b1.58

(1) Additions Instead Of Multiplications

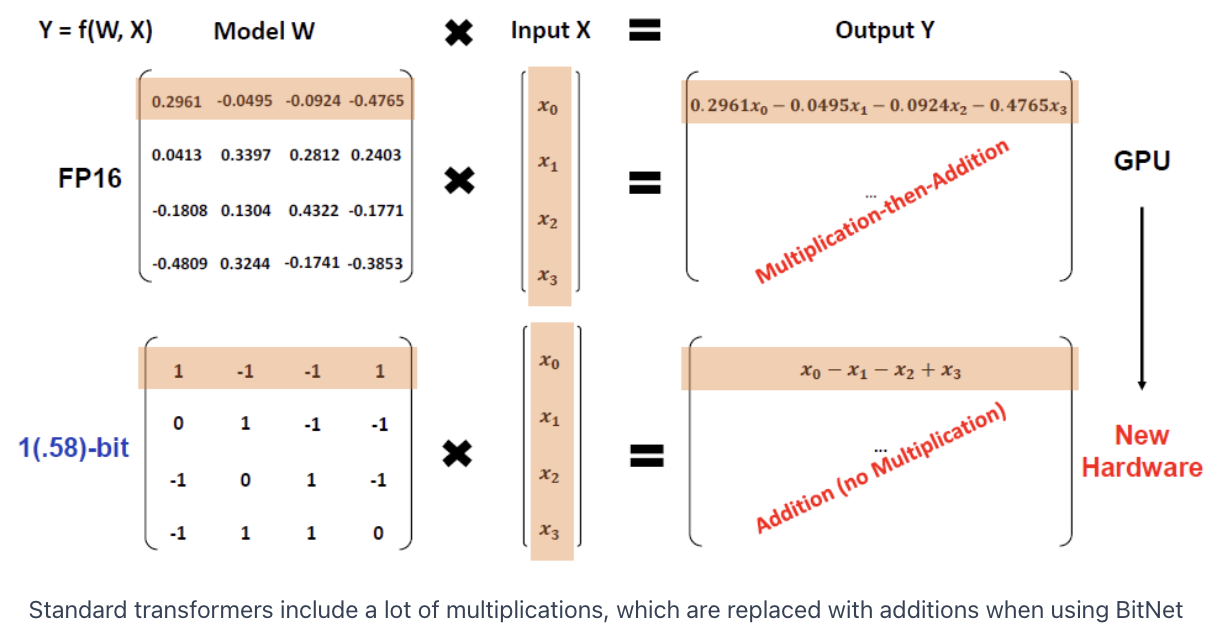
(2) Feature Filtering

Variant of the original BitNet model

• (Original) BitNet = Each weight is either -1 or 1

• (Proposed) BitNet 1.58 = Addition of 0

  \(\rightarrow\) Allows the model to filter out features & significantly improve the latency!

(3) Reduce Cost Without Performance Penalty

Can match full precision models performance

( while dramatically reducing the cost to tun the models )

4. Model Architecture

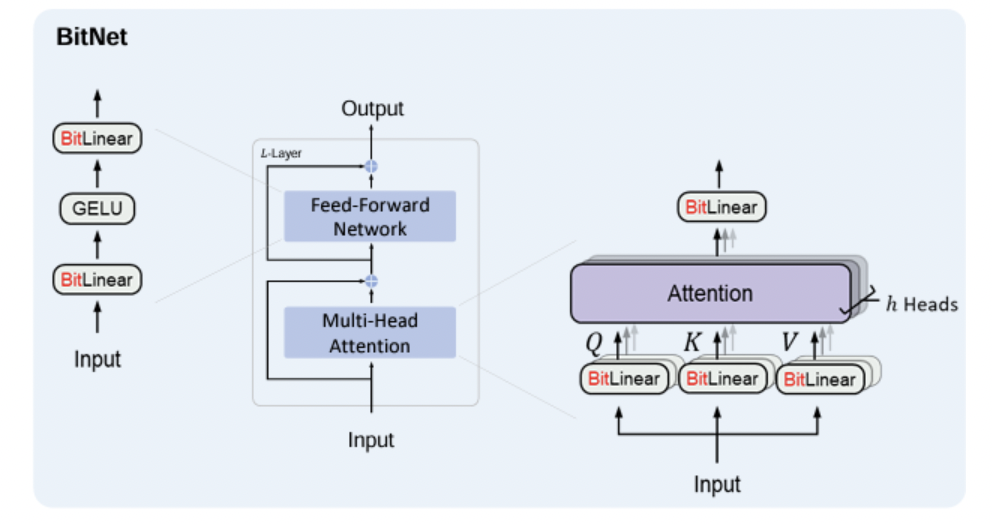
Same layout as transformers

• Stacking blocks of self-attention
• Feed-forward networks.

Difference?

• Instead of the regular matrix multiplication, use BitLinear

  \(\rightarrow\) Limit the model weights to the possible values of (-1,0,1)

Constrain weights to ternary values

\(\begin{gathered} \widetilde{W}=\operatorname{RoundClip}\left(\frac{W}{\gamma+\epsilon},-1,1\right), \\ \operatorname{RoundClip}(x, a, b)=\max (a, \min (b, \operatorname{round}(x))), \\ \gamma=\frac{1}{n m} \sum_{i j} \mid W_{i j} \mid . \end{gathered}\).

How to ensure that the weights will only be -1, 0 or 1?

\(\rightarrow\) Use absolute mean quantization.

• Step 1) Scale the weight matrix by its average absolute value.
• Step 2) Round each weight to the nearest number among the three possible options

5. Experiments