Fast Inference of Mixture-of-Experts Language Models with Offloading
Eliseev, Artyom, and Denis Mazur. "Fast inference of mixture-of-experts language models with offloading." arXiv preprint arXiv:2312.17238 (2023).
참고:
- https://aipapersacademy.com/moe-offloading/
- https://arxiv.org/pdf/2312.17238
Contents
- Motivation
- LLMs Are Getting Larger
- MoE Improves LLM’s Efficiency
- MoE on Limited Memory Hardware
- Mixture of Experts (MoE)
- Input Encoding vs. Tokens Generation
- Phase 1: Input Prompt Encoding
- Phase 2: Tokens Generation
- Speculative Experts Loading
1. Motivation
(1) LLMs Are Getting Larger
LLMs are getting larger and larger!
\(\rightarrow\) How to improve the efficiency of running LLMs?
(2) MoE Improves LLM’s Efficiency
Mixture of Experts (MoE)
-
Different parts of the model ( = experts ) learn to handle certain types of inputs
(+ Model learns when to use each expert)
-
For a given input, only a small portion of all experts is used
\(\rightarrow\) More compute-efficient!
-
e.g., Mixtral-8x7B.
(3) MoE on Limited Memory Hardware
MoE models = Have a large memory footprint
\(\because\) Need to load all of the experts into memory
This paper = How to efficiently run MoE models with limited available memory
\(\rightarrow\) With off-loading!
\(\rightarrow\) Allows running Mixtral-8x7B on the free tier of Google Colab
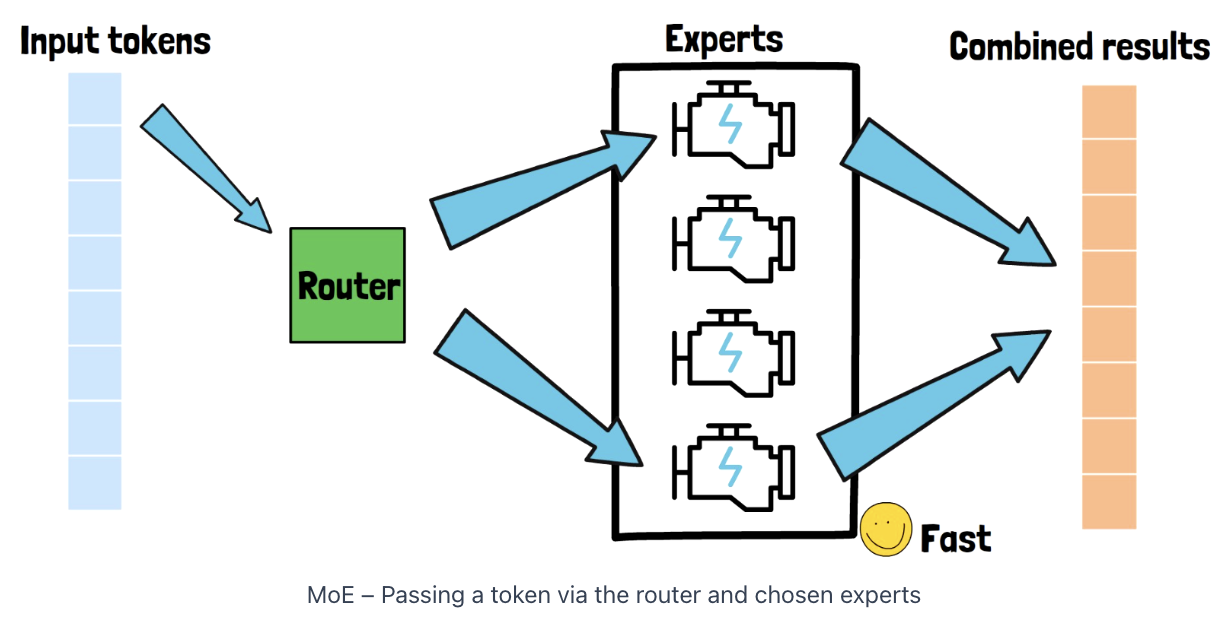
2. Mixture of Experts (MoE)
Common methods: sparse MoE
Key Idea: Instead of having one large model that handles all of the input space…
\(\rightarrow\) Divide the problem such that different inputs are handled by different experts
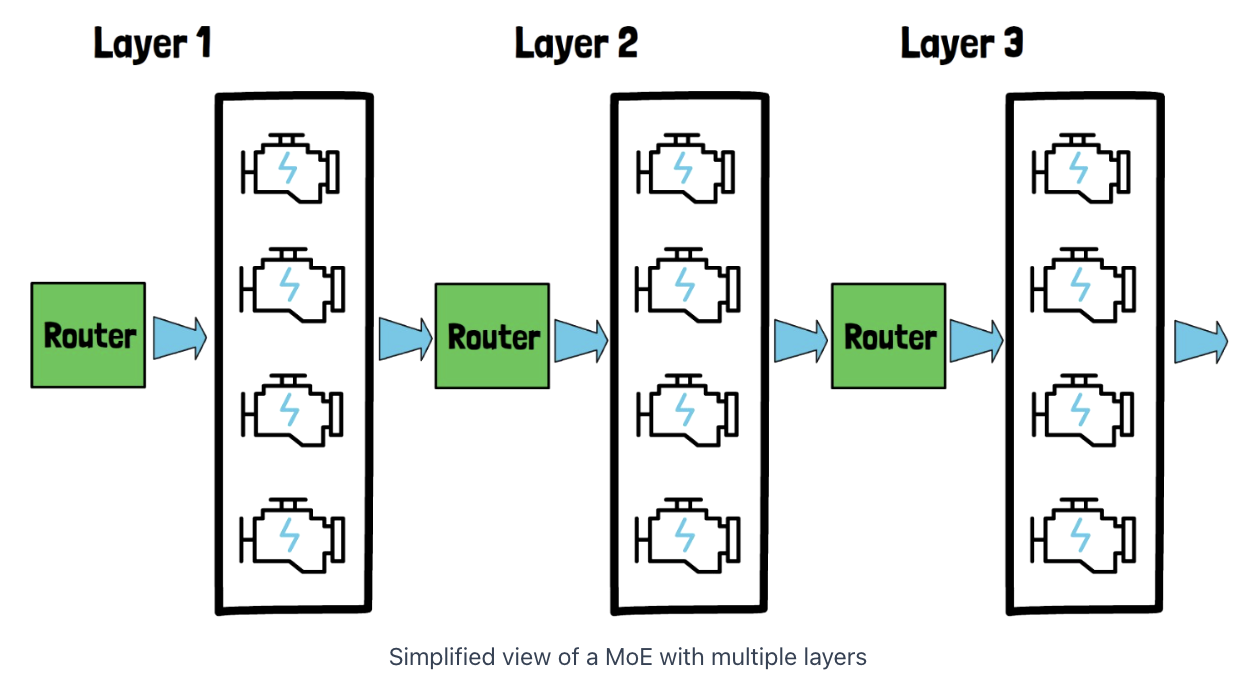
3. Input Encoding vs. Tokens Generation
[1] Input prompt: The tokens are handled together
\(\rightarrow\) Do not do this one after the other!
[2] Generated tokens:
\(\rightarrow\) Have to go through this process * token by token*
Example)
Offloading
Limited hardware: cannot load the entire model into GPU memory
\(\rightarrow\) Use “offloading”
-
(1) Offloading includes only the experts weights
( \(\because\) Experts weights are in charge for the majority of the model size )
-
(2) Keep the other parts of the model constant in the GPU
- e.g., routers, and self-attention blocks
(1) Phase 1: Input Prompt Encoding
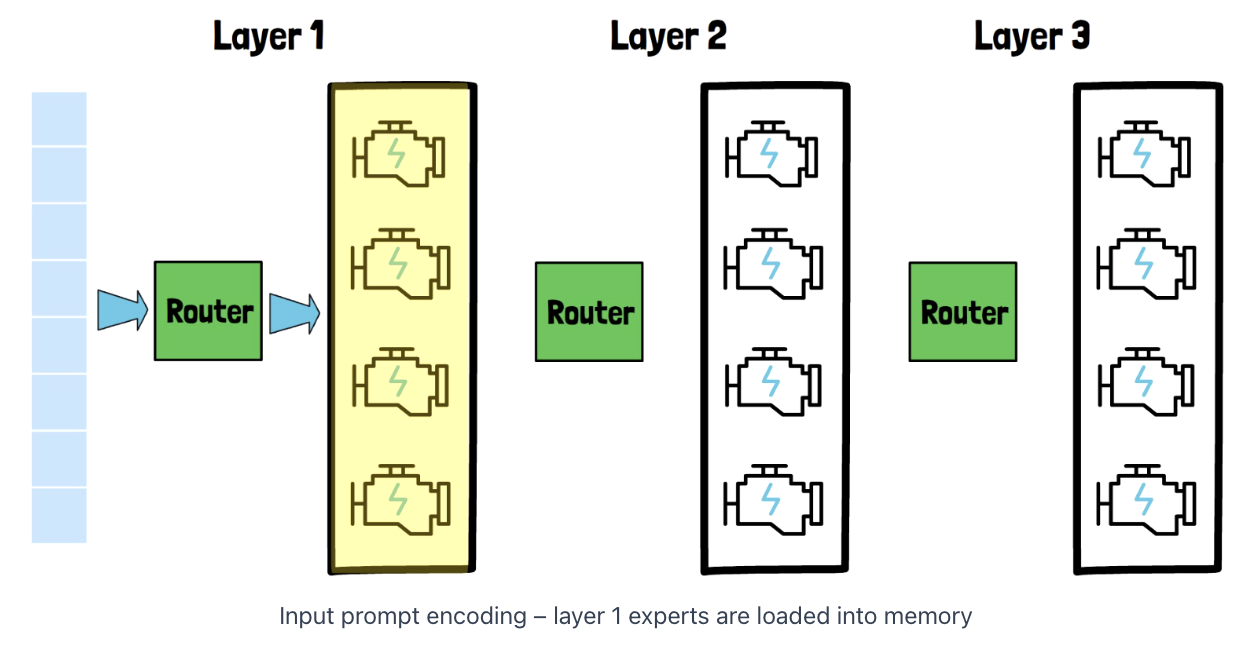
Simple offloading technique already works quite well!
Procedure
- Step 1-1) Load the experts of layer 1 into memory
- Step 1-2) Once finished, layer 1 experts can be unloaded
- Step 2-1) Load the experts of layer 2 into memory
- Step 2-2) Once finished, layer 2 experts can be unloaded
- …
Each layer experts are loaded only once, since we process the input sequence in parallel and layer by layer
(2) Phase 2: Tokens Generation
Layer by layer & Token by Token
LRU cache
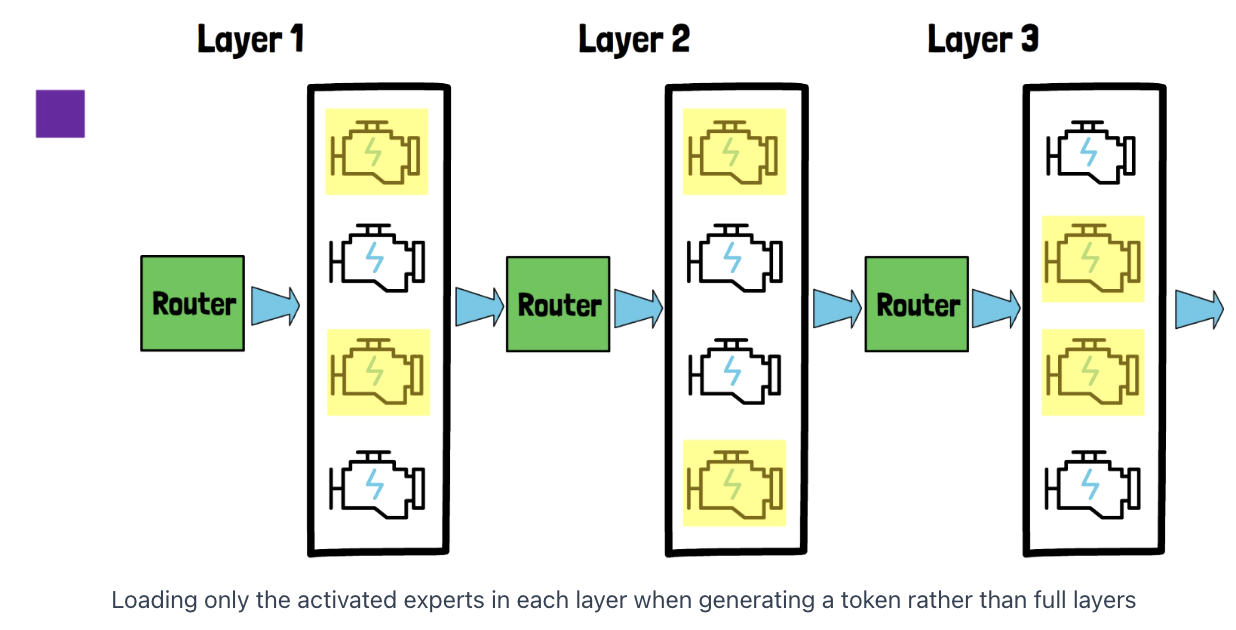
(LRU cache size is 2 for all layers)
Procedure (for first token)
-
Step 1) First layer: Only partial experts are loaded!
- e.g., activated experts = [1,3]
-
Step 2) Second layer: Only partial experts are loaded!
- e.g., activated experts = [1,4]
….
Key point: If we want to only load the activated experts, we have to wait for the results of the first layer, since choosing the activated experts by the router is based on the previous layer output
Procedure (for second token)
-
Step 1) We already have 2 experts loaded in the first layer!
-
e.g., should activate experts [1,2] & [1,3] are already activated!
\(\rightarrow\) offload [3], & load [2]
-
-
Step 2) same ~
LRU cache hit rate is large
= Many cases where the activated expert is already loaded when we need it
\(\rightarrow\) Improves the efficiency of the inference process
(3) Example
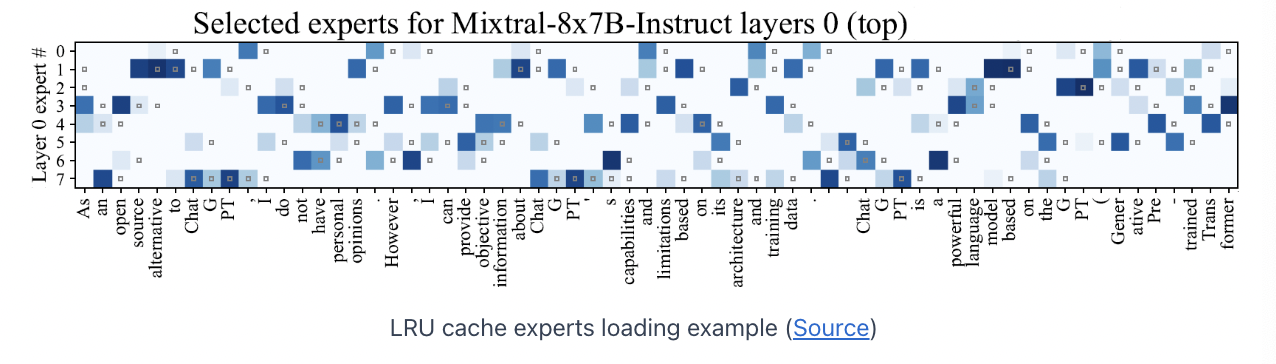
4. Speculative Experts Loading
Another method to accelerate the model!
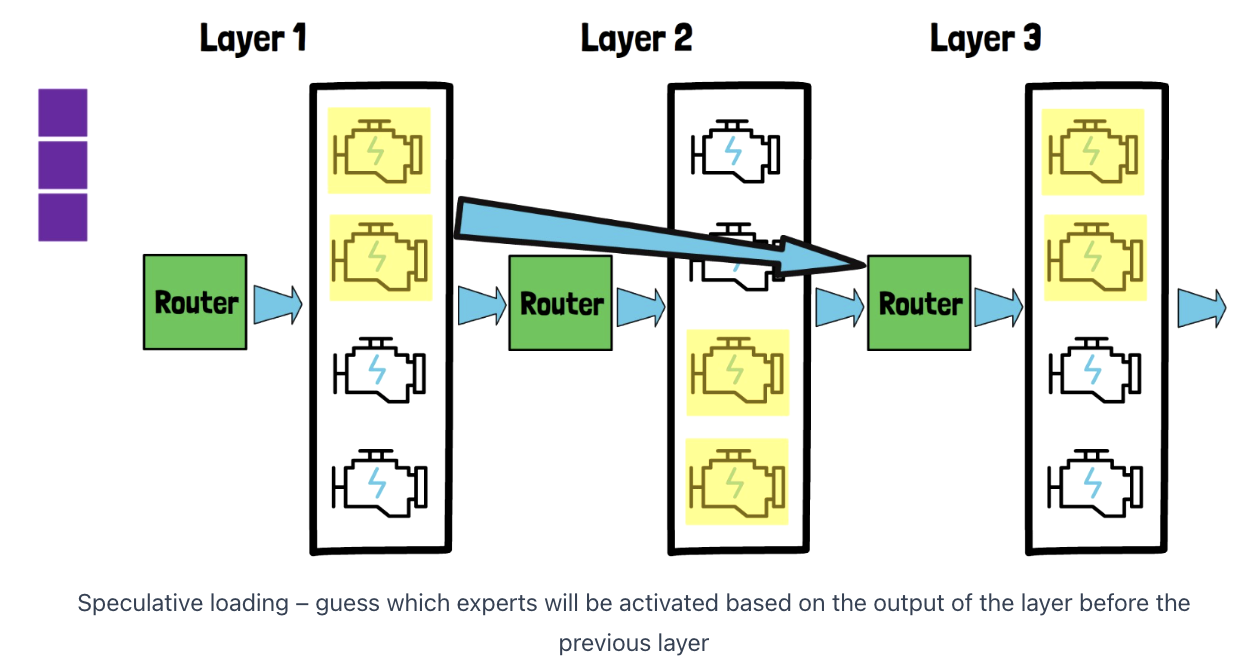
Section 3: If there is no change from before .. still use the LRU cache \(\rightarrow\) Efficient!
Key Idea: Guess which experts will be used !
( Rather than waiting for the results from previous layer )
Experiments
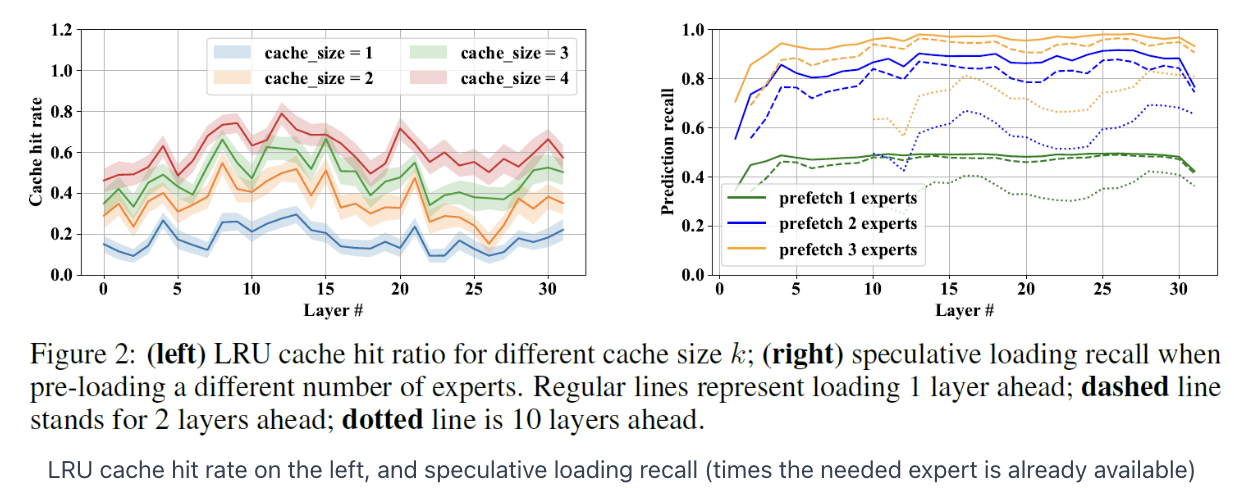
If we prefetch the experts of {n} layer ahead based on the speculative loading guess:
-
n=1 : correct expert loaded for about 80%
-
n=3 : correct expert loaded for about 90%
