Titans: Learning to Memorize at Test Time
Behrouz, Ali, Peilin Zhong, and Vahab Mirrokni. "Titans: Learning to Memorize at Test Time." arXiv preprint arXiv:2501.00663 (2024).
참고:
- https://aipapersacademy.com/titans/
- https://arxiv.org/pdf/2501.00663
Contents
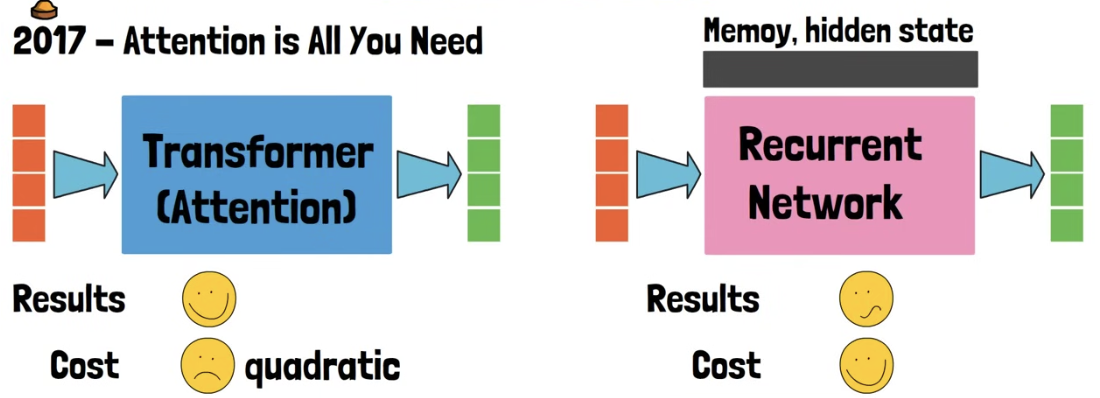
- Transformer vs. RNN
- Deep Neural Long-Term Memory Module
- Memorization w/o overfitting
- Modeling Surprise
- Modeling Past Surprise
- Modeling Forgetting
- The Loss Function
- Titan Architecture #1: MAC
- Titan Architecture #2: MAG
- Titan Architecture #3: MAL
1. Transformer vs. RNN
2. Deep Neural Long-Term Memory Module
Titans
- (1) Promising results & (2) Mitigate the quadratic complexity
- Inspiration: How memory works in the human brain
Key contribution of Titan = Deep Neural Long-Term Memory Module
-
RNN: memory = fixed vector
-
Neural long-term memory module: memory = model
\(\rightarrow\) Encodes the abstraction of past history into its parameters
How to train such model??
\(\rightarrow\) Train the model to memorize its training data!
\(\rightarrow\) Then… what if overfitting issue?
(1) Memorization w/o overfitting
How to create a model capable of memorization, but without overfitting?
\(\rightarrow\) Inspired by an analogy from human memory!
Human:
- When we encounter an event that surprises us, we are more likely to remember that event.
\(\rightarrow\) That’s how the neural long-term memory module is designed!
Updating the neural memory with a surprise element!
(2-1) Modeling Surprise
\(\mathcal{M}_t=\mathcal{M}_{t-1}-\theta_t \underbrace{\nabla \ell\left(\mathcal{M}_{t-1} ; x_t\right)}_{\text {Surprise }}\).
- \(\mathcal{M}_t\): Neural long-term memory module at time \(t\)
- Surprise element = gradient
- High gradient = More surprised by input \(\rightarrow\) More update in params
\(\rightarrow\) Not ideal!
( \(\because\) Model may miss important information happening right after the surprising moment happened )
\(\mathcal{M}_t=\mathcal{M}_{t-1}+S_t\).
\(S_t = -\theta_t \underbrace{\nabla \ell\left(\mathcal{M}_{t-1} ; x_t\right)}_{\text {Surprise }}\).
(2-2) Modeling Past Surprise
Human:
- Surprising event will not last long! ( although it remains memorable )
- Nevertheless, the event may be surprising enough to get our attention through a long memory!
\(\mathcal{M}_t=\mathcal{M}_{t-1}+S_t\).
Update params using (1) & (2)
- (1) State of the previous weights (\(\mathcal{M}_{t-1}\))
- (2) Surprise component (\(S_t\))
Modeling Surprise vs. Modling Past Surprise
-
Modeling Surprise: \(S_t = -\theta_t \underbrace{\nabla \ell\left(\mathcal{M}_{t-1} ; x_t\right)}_{\text {Surprise }}\).
-
Modeling Past Surprise: \(S_t=\eta_t \underbrace{S_{t-1}}_{\text {Past Surprise }}-\theta_t \underbrace{\nabla \ell\left(M_{t-1} ; x_t\right)}_{\text {Momentary Surprise }}\).
- Included the modeling of past surprise ( with a decay factor )
(2-3) Modeling Forgetting
Not done yet! Humans do forget!
When dealing with very large sequences …
\(\rightarrow\) Crucial to manage which past information should be forgotten!!!
\(\mathcal{M}_t=(1-\alpha_t)\cdot \mathcal{M}_{t-1}+S_t\).
\(S_t=\eta_t \underbrace{S_{t-1}}_{\text {Past Surprise }}-\theta_t \underbrace{\nabla \ell\left(M_{t-1} ; x_t\right)}_{\text {Momentary Surprise }}\).
Update params using (1) & (2)
- (1) State of the previous weights (\(\mathcal{M}_{t-1}\)) + adaptive forgetting mechanism
- \(\alpha_t\) : Gating mechanism
- Allows the memory to be forgotten
- (2) Surprise component (\(S_t\))
(3) The Loss Function
Goal of model:
- (1) Aims to model associative memory
- By storing the past data as pairs of keys and values
- (2) Teach the model to map between keys and values.
\(\ell\left(\mathcal{M}_{t-1} ; x_t\right)= \mid \mid \mathcal{M}_{t-1}\left(\mathbf{k}_t\right)-\mathbf{v}_t \mid \mid _2^2\).
- \(\mathbf{k}_t=x_t W_K\).
- \(\mathbf{v}_t=x_t W_V\).
Details
-
Linear layers project the input into keys and values
-
Loss = Measures how well the memory module learns the associations between keys and values
Note that the model does not process the entire sequence at once
( Processes it gradually to aaccumulate memory information in its weights )
3. Titan Architecture #1: MAC
Memory as a Context (MAC)
3 components
- (1) Persistent memory
- (2) Core
- (3) Contextual memory
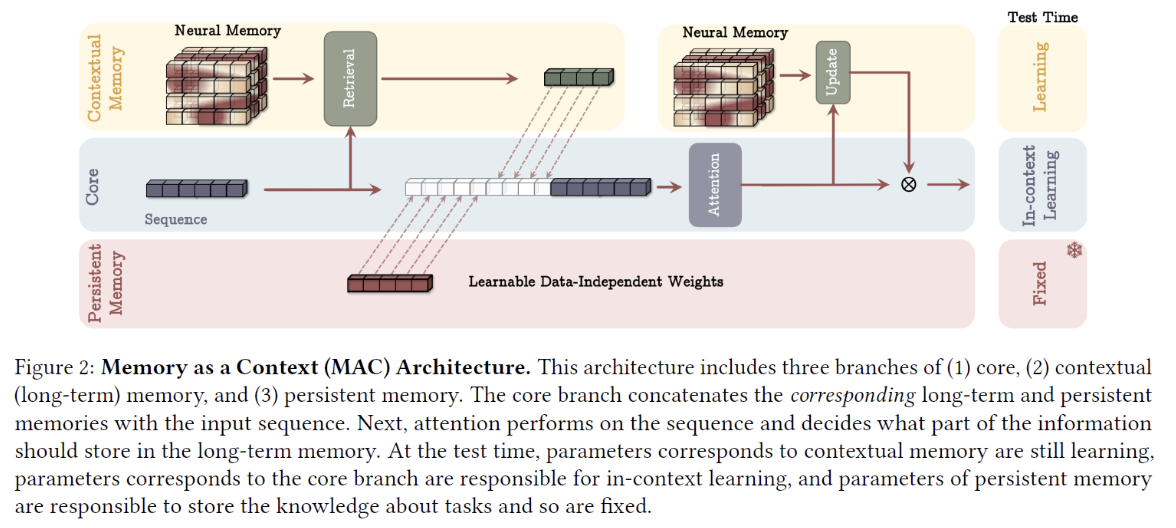
Procedure
-
Step 1) Chunk a long input sequence (= (A) )
- Sequence at core: A (single) chuncked sequence
-
Step 2-1) **[Contextual memory] **
Retrieve memory from contextual memory with a chunk ( = (B) )
-
Step 2-2) [Persistent memory]
Add (learnable) data-independent weights = ( = (C) )
-
Step 2-3) Concatenated result: [(A),(B),(C)]
-
Step 3) Pass [(C),(B),(A)] via an attention block
(1) Persistent memory
-
Data-independent = global information ( = not impacted by the input )
-
At the beginning of the sequence
\(\rightarrow\) Helps avoid attention drain (feat. Hymba)
(2) Contextual memory
Consists of the deep neural long-term memory module
Retrieve memory tokens from the contextual memory
-
By a forward pass of the neural long-term memory module
-
Input: chunked sequence ( = (A) )
-
Neural memory: keeps being updated even in test time
\(\rightarrow\) Note that the neural memory is already updated with previous chunks (of the same sequence) !
-
(3) The Core component
Role: brings it all together
-
Using an attention block
-
Input = Extended sequence [(C),(B),(A)]
-
Contains information from all!
-
(C) Persistent memory
-
(B) Contextual memory
-
(A) Input itself
-
\(\rightarrow\) The model can leverage multiple memory types!
-
-
Output = Used to update the neural memory
- Helps to determine for a given input …
- ,Whether the long-term memory should be used or not.
- Helps the long-term memory to store only useful information from the current context.
- Helps to determine for a given input …
Final output: based on (1) & (2)
- (1) Output from the attention block
- (2) Output from the neural memory
4. Titan Architecture #2: MAG
Memory as a Gate (MAG)
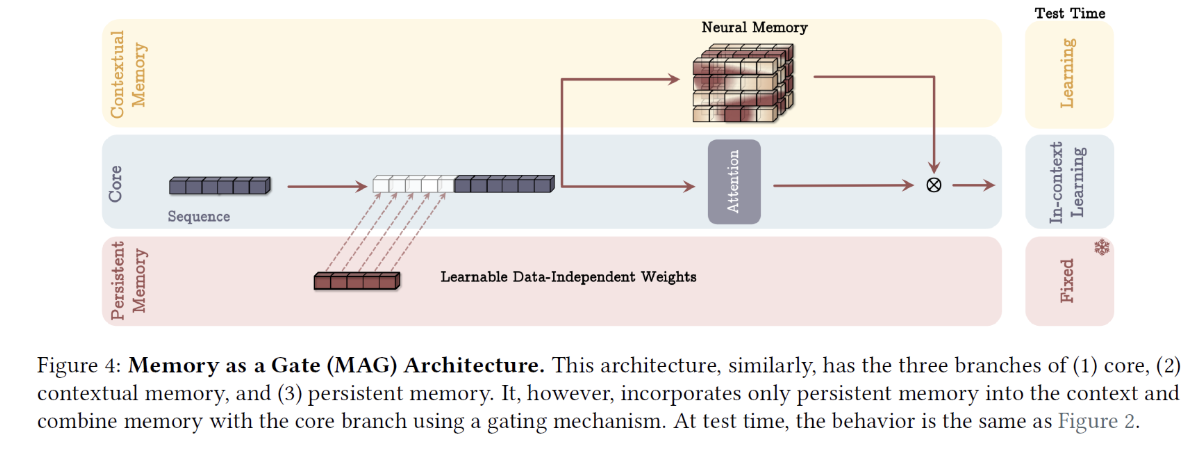
(Like MAC) Also have 3 branches
- (1) Persistent memory
- (2) Core
- (3) Contextual memory
Difference with MAC:
-
(1) Input sequence is not chunked
-
Full input sequence
-
How? By utilizing sliding window attention in the attention block
-
-
(2) Neural memory does not contribute data into the context for the attention block
- Neural memory is only updated from the input sequence
5. Titan Architecture #3: MAL
Memory as a Layer (MAL)
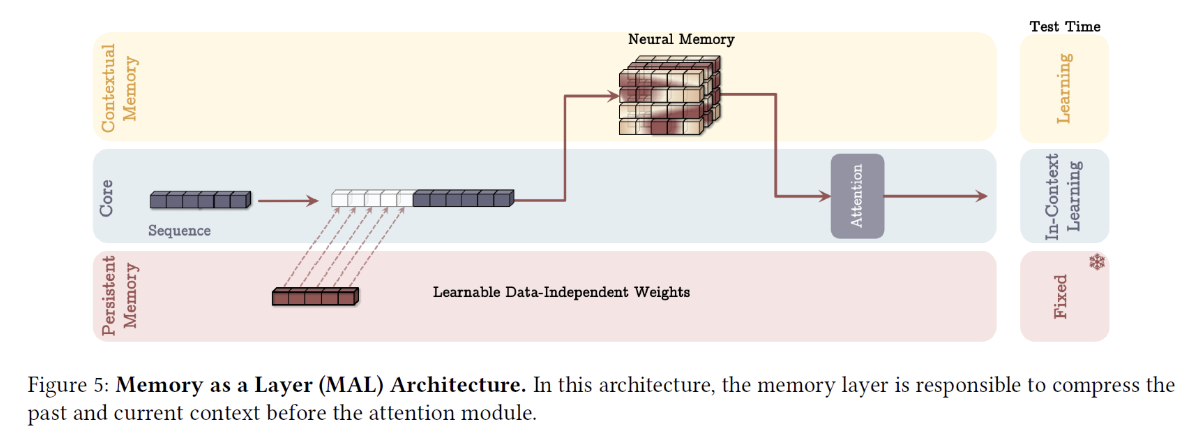
(Like MAC) Also have 3 branches
- (1) Persistent memory
- (2) Core
- (3) Contextual memory
Similar to MAL:
- (1) Input sequence is not chunked
Difference with (2):
- Neural memory as a model layer!
