Chronos-2; From Univariate to Universal Forecasting

Chronos-2: From Univariate to Universal Forecasting

https://arxiv.org/pdf/2510.15821

Abstract

• TSFM은 (task-specific training 없이도) inference-only forecasting을 가능하게 함
• 기존 TSFM: Univariate forecasting에 집중
• Chronos-2:
  • 세 가지 모두 가능
    • a) Univariate
    • b) Multivariate
    • c) Covariate-informed
  • Zero-shot으로 처리 가능한 Universal forecasting model
• 핵심: Group attention
  • 여러 TS 간 Information sharing을 가능하게 함
  • 하나의 group은 다음을 의미할 수 있음
    • 관련된 여러 series 집합
    • MTS의 variates
    • Target과 covariates의 결합
  • 이를 통해 In-context learning (ICL)이 효과적으로 작동함
• Pretraining Dataset
  • Real dataset (X)
  • Synthetic datasets (O)
  • Univariate series에 다양한 Multivariate structure를 인위적으로 부여
• 성능 평가
  • fev-bench, GIFT-Eval, Chronos Benchmark II에서 SoTA
  • 특히 fev-bench에서 강점이 두드러짐
    • Multivariate
    • Covariate-informed forecasting 중심 벤치마크

1. Introduction

(1) Pretrained TSFM

• (1) 개별 TS마다 학습하는 Local models

• (2) 데이터셋마다 학습하는 Task-specific models

  → (1) & (2) 하나의 모델을 대규모 데이터로 한 번 학습 후 다양한 문제에 적용 가능

• (3) Pretrained 모델의 장점

  • Forecasting pipeline 단순화
  • 매번 학습할 필요 없음
  • 많은 경우 task-specific 모델과 동등하거나 더 높은 정확도 달성

(2) Limitation of TSFM

대부분이 Univariate forecasting만 지원

실제 환경에서는

• Multivariate forecasting
• Covariate-informed forecasting

Universal pretrained model이 어려운 이유?

• (1) Architecture 문제
  • Task마다 변수 개수와 의미가 다름
  • 변수 간 상호작용을 사전에 정의할 수 없음
  • 모델이 context로부터 관계를 추론해야 함
• (2) Data 문제
  • Multivariate 구조와 informative covariate를 포함한 고품질 데이터가 부족함

(3) Proposal: Chronos-2

Chronos-2

• Univariate, Multivariate, Covariate-informed forecasting을 모두 지원
• Zero-shot으로 동작

주요 특징

• In-context learning (ICL) 기반
• Past-only covariate와 future-known covariate 모두 처리 가능
• Real-valued 및 categorical covariate 모두 지원

ICL의 추가 효과

• Univariate forecasting에서도 Cross-learning 발생
• 배치 내 여러 TS 간 정보 공유를 통해 정확도 향상

핵심 메커니즘: Group attention

• Group은 다음을 모두 의미할 수 있음
  • 관련된 여러 TS
  • MTS의 variates
  • Target과 covariates의 조합
• 단순 concat 방식이 아닌
  • Batch axis를 통한 정보 공유
  • Variate 수 증가에도 잘 확장됨

Training strategy

• 실제 multivariate 데이터에 의존하지 않음
• Univariate generator에서 샘플링한 series에
  • Synthetic multivariate structure를 부여
• 이를 통해 ICL 능력을 학습

실험 결과

• fev-bench, GIFT-Eval, Chronos Benchmark II에서 SOTA 달성
• fev-bench 전 범주에서 baseline 대비 우수
• 특히 Covariate-informed task에서 가장 큰 성능 향상

효율성

• 단일 중급 GPU (NVIDIA A10G)에서 실행 가능
• 초당 약 300 TS 처리

2. Background and Related Works

(1) Background

Notation

• [Input] \(\mathbf{Y}_{1:T} = [y_1, \ldots, y_T]\).
  • \(y_t \in \mathbb{R}^D\).
  • Univariate: \(D = 1\)
  • Multivariate: \(D > 1\)

• [Target] \(\mathbf{Y}_{T+1:T+H}\).

• [Covariates (Exogenous Variables)] \(\mathbf{X}_{1:T+H} = [x_1, \ldots, x_{T+H}]\):
  • \(x_t \in \mathbb{R}^M\).
  • 예측을 보조하는 추가 정보
  • 과거 시점 t \le T와 미래 시점 t > T 모두 포함 가능

Forecasting 유형

• Point forecasting
• Probabilistic forecasting

Summary

• \(P(\mathbf{Y}_{T+1:T+H} \mid \mathbf{Y}_{1:T}, \mathbf{X}_{1:T+H})\).

(2) Related Works

기존 Forecasting 방법의 구분

• a) Local models
  • 각 TS마다 개별 파라미터를 학습
  • e.g.,) ARIMA, Exponential Smoothing
  • 장점: 단순, 해석 용이
  • 한계:
    • 데이터가 많아질수록 확장성 부족
    • TS 간 정보 공유 불가

• b) Global models

  • 하나의 모델이 데이터셋 내 모든 TS의 파라미터를 공유
  • DL 기반 접근이 주류
  • 대표 예시: RNN, Transformer 등의 구조

• c) Pretrained TSFMs

  • 대규모 TS 데이터로 한 번 학습 후 zero-shot 사용

  • LLM과 유사한 패러다임
    • task별 재학습 불필요
    • 다양한 데이터셋에 일반화

  • 초기 시도: LLM을 TS에 직접 적용

  • 최근 추세
    • LLM 구조를 차용
    • 학습은 TS 데이터로만 수행
  • 한계: 대부분 Univariate forecasting에만 특화

대표적인 TSFMs

• Moirai-1
  • Multivariate 입력 지원
  • 내부적으로 flatten 처리
  • 고차원 변수에서 확장성 제한
• Toto
  • Cross-variate attention 도입
  • Known / categorical covariate 미지원
• COSMIC
  • Synthetic augmentation으로 covariate 활용
  • Target은 univariate로 제한
• TabPFN-TS
  • Known covariate 사용 가능
  • Past-only covariate, multivariate target 미지원

Summary

• 대부분 univariate 대비 성능 개선이 제한적

• Zero-shot 환경에서

  • multivariate

  • covariate

    를 동시에 잘 처리하는 모델은 여전히 부족

(3) Chronos-2의 포지션

• 문제 인식: Multivariate + covariate를 zero-shot으로 통합 처리하는 것이 미해결 문제

• 제안: Group Attention Mechanism

  • 관련된 TS들을 group 단위로 묶어 처리
  • Univariate / Multivariate / Covariate-informed 설정을
    • 동일한 아키텍처
    • 추가 수정 없이 처리
  • 기존 cross-attention 및 cross-learning 아이디어를 일반화

3. Chronos-2

(1) Scaling and Tokenization

핵심 목표

• (1) Univariate / Multivariate / Covariate-informed forecasting을 하나의 입력 표현으로 통합

• Zero-shot 환경에서도

  • 스케일 차이
  • 결측
  • 미래에 알려진 covariate

  를 안정적으로 처리

a) Input Construction

Historical input

• \[V = [v_1, \dots, v_T], \quad v_t \in \mathbb{R}^{D+M}\]
• \(y_t\) (target) with \(D\) dim
• \(x_t\) (covariates) with \(M\) dim

Future input

• \[W = [w_{T+1}, \dots, w_{T+H}], \quad w_t \in \mathbb{R}^{D+M}\]
• known future covariates만 유지
• target 및 past-only covariates는 missing 처리

Summary: Target과 covariate를 동일한 차원에서 다룸

b) Categorical Covariates

Univariate target

• Target encoding 사용

  • category를 target과의 통계적 관계 기반 수치로 변환

Multivariate target

• Ordinal encoding 사용

  • category마다 고유 integer 할당

• 목적

  • 다양한 categorical covariate를 zero-shot 환경에서도 안전하게 처리

c) Robust Scaling

문제의식: 금융, 에너지, 리테일 데이터는 아래의 issue!

• scale 불균형

• outlier

Procedure

• Step 1) Standardization
  • historical context 기준

• Step 2) sinh⁻¹ 변환

  • log-like 변환

  • extreme value 영향 완화
  • \(\tilde v_{t,d} = \sinh^{-1}\left(\frac{v_{t,d} - \mu_d}{\sigma_d}\right), \quad \tilde w_{t,d} = \sinh^{-1}\left(\frac{w_{t,d} - \mu_d}{\sigma_d}\right)\).

Results

• scale 안정화
• outlier 민감도 감소
• 학습 및 추론 안정성 향상

d) Meta Features

• 각 차원 \(d\)에 대해 독립적으로 처리, 추가 정보 부착

• Time index
• 상대적 위치 인코딩
  • patch 기반 입력에서 temporal order 명시적 제공
• Mask

  • 관측 여부 표시

  • 역할

    • historical missing value 식별
    • future-known covariate 구분

• 처리 방식

  • missing value는 0으로 치환
  • mask가 정보 손실 방지

e) Patching and Embedding

• PatchTST 계열 전략 채택

  • patch length \(P\)
  • non-overlapping

• Context와 Future를 분리해서 patching

• Procedures

  • Step 1) Patch 구성: p-번째 patch

    • 입력값 patch: \(\bar{u}_p\)

    • 시간 index patch: \(\bar{j}_p\)

    • mask patch: \(\bar{m}_p\)

    • 세 요소를 concatenate

  • Step 2) Patch Embedding

    • Residual network \(f_\phi\)
    • \(h_p = f_\phi^{\text{in}} \big( [\bar{u}_p, \bar{j}_p, \bar{m}_p] \big), \quad f_\phi^{\text{in}} : \mathbb{R}^{3P} \rightarrow \mathbb{R}^{D_{\text{model}}}\).

• 의미

  • raw value

  • temporal position

  • observability

    를 하나의 토큰 표현으로 통합

• REG Token

  • context patch와 future patch 사이에 삽입

  • 역할
    • separator token
    • attention sink
  • 효과
    • context 정보를 안정적으로 집약
    • future forecasting 시
      • 불필요한 attention 확산 방지
      • inference 안정성 향상

(2) Architecture

전체 구조

• Encoder-only: T5 기반
• 핵심 아이디어
  • Time Attention + Group Attention을 교차적으로 쌓아
  • In-context learning(ICL)을 구조적으로 구현

a) Time Attention

• 시간 축(temporal axis) 기준 self-attention
• 동일한 input dimension 내에서
  • patch 간 temporal dependency 집계
• Position Encoding
  • (X) T5의 relative position embedding
  • (O) RoPE (Rotary Position Embedding)

b) Group Attention

• 목적
  • 같은 time index의 patch들 간 정보 공유
  • (시간 축이 아니라) series / variate / covariate 축에서 attention
• 작동 방식
  • 동일한 patch index에서
    • 같은 group ID를 가진 TS들만 attention
• Positional embedding (X)
  • 이유: group 내부 TS에는 자연스러운 순서가 없음

Group의 정의 (task-dependent)

Group은 “서로 정보를 공유해야 할 대상들의 집합”

상황에 따라 다르다!

• Single TS
  • Univariate forecasting
  • 다른 TS 참조 없음
• Related TS set
  • 동일 source / metadata
  • Cross-learning, Few-shot forecasting
  • Cold-start 상황에 특히 유리
• Variates with shared dynamics
  • multivariate forecasting
  • 여러 변수의 공동 예측
• Targets + covariates
  • 가장 일반적인 설정
  • target
  • past-only covariates
  • known future covariates

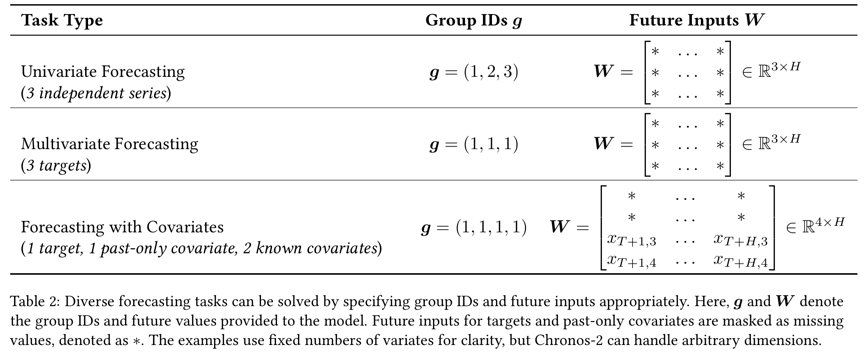
Group Attention 구현 디테일

• Batch size: \(B\)
• Group ID
  • 길이 \(B\)의 벡터 \(g\)
• 내부 처리
  • Group ID → 2D attention mask
  • 서로 다른 group 간 attention 완전 차단
• 결과
  • Task-specific architecture 변경 없이
  • 다양한 forecasting setting 지원

c) Quantile Head

• Input

  • Future patch embeddings
  • Target dimension \(D\)만 사용

• Output

  • Direct multi-step & quantile forecast

• 출력 형태

  • \(\hat{Z} \in \mathbb{R}^{H \times D \times \mid \mathcal{Q} \mid}\).

  • Quantile set: \(\mathcal{Q} = \{0.01, 0.05, 0.1, \dots, 0.9, 0.95, 0.99\}\)

    • 총 21 quantiles

    • 기존 pretrained TS 모델(보통 9개 quantile)보다 조밀

(3-1) Training Overview

학습 설정 개요

• 하나의 Model, 여러 forecasting task를 동시에 학습
• Batch 구성 시, 다음 task들을 혼합:
  • (1) Univariate forecasting
  • (2) Multivariate forecasting
    • past-only covariates 포함
  • (3) Multivariate forecasting with known covariates

각 task의 정의

• 타겟 차원 수: \(D\)
• Covariate 수: \(M\)
• 각 dimension의 역할:
  • Target
  • Past-only covariate
  • Known future covariate

Task 식별 방식 (암묵적 task inference)

• 각 task에 고유한 group ID 할당
• 모델은 다음 정보를 통해 task 구조를 추론:
  • (1) Group ID \(g\)
  • (2) Future input \(W\)의 관측 여부
• 결과
  • Task-specific head나 architecture 변경 X
  • Forecasting setup을 in-context로 인식

Loss function: Quantile Regression

• 사용 목적

  • probabilistic forecasting
  • 다중 quantile 직접 예측

• 손실 함수

  • $$\ell_q(z, \hat{z}_q)

    q \cdot \max(z - \hat{z}_q, 0) + (1 - q) \cdot \max(\hat{z}_q - z, 0), \quad q \in \mathcal{Q}$$.

    • \(\hat{z}_q\): quantile q에서의 예측값

    • \(z\): Eq. (1)로 정규화된 실제 target 값

Loss 계산 방식

• a) Forecast horizon 전체에 대해 평균
• b) Batch 내 모든 item에 대해 평균
• c) Target dimension에 대해서만 계산
• (다음 항목은 loss에서 제외)
  • known covariates
  • missing target values

(3-2) Training Details

a) Output Patch Sampling

• 의미? 각 batch마다, 출력 patch 수를 랜덤 샘플링
• 효과
  • 다양한 horizon 길이에 대한 일반화
  • 특정 horizon에 과적합 방지

b) Two-Stage Training Strategy

Stage 1: Base Pretraining

• 최대 context length: 2048
• 최대 output patch 수: 작게 제한
• 목적
  • 기본적인 TS 패턴 학습
  • 안정적인 초기 수렴

Stage 2: Long-context & Long-horizon Training

• context length 확장: \(2048 \rightarrow 8192\)

• 최대 output patch 수 증가
• 효과
  • 장기 seasonal pattern 학습 (고빈도 TS)
  • heuristic 없이 장기 예측 가능

Summary

• Chronos-2는

  • task를 명시적으로 알려주지 않아도

  • group ID + mask 구조로

    forecasting setup을 스스로 추론

• 학습 단계에서부터

  • universal forecasting 능력을 강제

• 긴 context + multi-patch output

  • Real-world long-horizon forecasting에 직접 대응

(4) Inference

a) Denormalization

De-normalization

• Model output: Normalized quantile prediction \(\hat{z}_{t,d}^q\)
• Denormalization
  • \(\hat{y}_{t,d}^q = \mu_d + \sigma_d \cdot \sinh(\hat{z}_{t,d}^q)\).t

Inference 시 grouping의 역할

• Batch 내 multiple TS를 group ID로 묶는 방식만 바꾸어
  • 서로 다른 forecasting task를 동일 모델로 해결
• Group attention이 어떤 series 간에 정보 공유를 할지 결정

b) Forecasting Modes via Group IDs

(1) Univariate forecasting

• Batch의 각 item에 서로 다른 group ID 할당
• 결과
  • 각 TS는 완전히 독립적으로 처리
  • cross-series 정보 공유 없음

(2) Multivariate forecasting

• 같은 MTS에 속한 variate들은 같은 group ID
• 서로 다른 MTS는 서로 다른 group ID
• 결과
  • 동일 MTS 내 variate 간 dynamics 공유
  • Multivariate dependency 학습 가능

(3) Forecasting with covariates

• Target, past-only covariate, known covariate를 모두 같은 group ID로 묶음
• Future input \(W\)
  • Known covariate는 실제 future 값을 제공
• 결과
  • 모델은 covariate를 활용하여 target 예측
  • covariate에 대한 예측 출력은 무시

c) Additional Mode: Full Cross Learning

Full cross learning mode

• Batch 내 모든 item에 동일한 group ID 할당

• Target 여부나 covariate 여부와 무관

• 효과
  • Batch 전체에서 정보 공유
  • Joint prediction 수행
  • Few-shot learning 및 domain shift 상황에서 특히 유용

4. Training Data

세 줄 요약

• Chronos-2와 같은 Generalist TSFM에서는 architecture보다 training data가 더 결정적
• 기존 대규모 TS 데이터셋은 대부분 univariate에 치우쳐 있음
• 이를 보완하고 in-context learning 능력을 부여하기 위해 synthetic data를 대규모로 활용

(1) Univariate Data

두 가지로 구성

• [1] Real-world datasets
• [2] Synthetic datasets

[1] Real-world datasets

• 기존 Chronos (Ansari et al., 2024)
• GIFT-Eval (Aksu et al., 2024)
• 사용된 전체 데이터셋은 Appendix Table 6에 정리됨

[2] Synthetic datasets

• TSI (Trend, Seasonality, Irregularity)
  • 서로 다른 trend, seasonality, irregularity 성분을 무작위로 조합
  • 다양한 형태의 TS 패턴 생성
• TCM (Temporal Causal Model)
  • Temporal causal graph를 샘플링
  • Autoregression을 통해 TS 생성
  • Causal structure를 내포한 TS 생성이 목적
• 의도
  • Univariate 패턴의 다양성 확보
  • 실제 데이터 분포에 대한 과도한 의존 방지

(2) Multivariate Data

전부 synthetic data만 사용

핵심 개념: Multivariatizer

• Step 1) Base univariate series 여러 개를 샘플링
• Step 2) 그 사이에 의존성(dependency)을 인위적으로 부여

Step 1) Base univariate generators

• AR models
• ETS models
• TSI
• KernelSynth

Step 2) Multivariatizer 유형

• Cotemporaneous multivariatizer
  • 동일한 timestep에서 linear 또는 nonlinear transformation 적용
  • instantaneous correlation 유도
• Sequential multivariatizer
  • 시간 축을 따라 dependency 유도
  • lead–lag effects, cointegration 등 복잡한 multivariate 특성 생성

생성된 데이터의 활용

• (1) Multivariate tasks
  • 모든 variate를 prediction 대상으로 설정
• (2) Covariate-informed tasks
  • 일부 variate를 무작위로 known covariate로 지정
  • Target과 covariate를 함께 포함한 forecasting 설정 구성

5. Experiments

Goal: Chronos-2의 성능을

• 대규모 benchmark
• ICL 효과
• 실제 도메인 (energy, retail)
• ablation 설정

에서 체계적으로 검증

구성

• 5.1 SoTAt 모델들과의 benchmark 비교
• 5.2 ICL 효과 분석 (univariate / multivariate / covariates)
• 5.3 Energy 및 retail case study
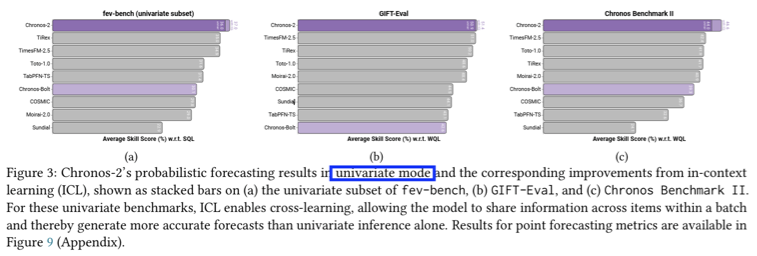
• 5.4 Ablation study
  • Smaller model
  • Synthetic-only training
  • Long-context post-training 이전 모델

(1) Benchmark Results

a) Experimental Setup

• 모델: Chronos-2 base (120M)
• Benchmarks
  • a) fev-bench
  • b) GIFT-Eval
  • c) Chronos Benchmark II

b) Evaluation Metrics

• Win rate \(W\): Pairwise 비교에서 상대 모델을 이긴 비율
• Skill score \(S\): Seasonal Naive 대비 평균 성능 향상률

c) Results with fev-bench

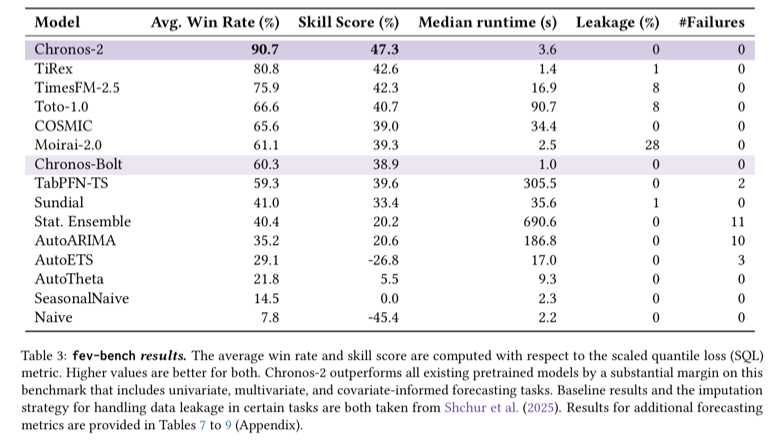
fev-bench

• 100 forecasting tasks
• covariate-informed task 포함
• Chronos-2는 해당 데이터셋을 훈련 중 전혀 보지 않음

Metric: Scaled Quantile Loss (SQL)

• Probabilistic forecasting 평가

결과: 모든 기존 foundation model 대비

• win rate
• skill score

에서 큰 폭으로 우수

d) Results with GIFT-Eval

GIFT-Eval

• 97 tasks
• 55 datasets
• high-frequency + long-horizon forecasting 중심

Metrics:

• Weighted Quantile Loss (WQL)
• Mean Absolute Scaled Error (MASE)

결과

• 기존 최고 성능 모델(TiRex, TimesFM-2.5) 대비

  • win rate
  • skill score

  모두에서 우수

Zero-shot 관련 주의

• Pretraining corpus가
  • 일부 dataset의 training split과는 partial overlap 존재
  • test split과는 overlap 없음
• Strictly zero-shot 결과
  • Section 5.4 (synthetic-only 모델)에서 별도 분석

e) Results with Chronos Benchmark II

Chronos Benchmark II

• 27 tasks
• 평균 history length < 300
• short-context 중심 benchmark

Metrics

• Probabilistic: WQL
• Point forecast: MASE

결과

• 모든 기존 모델 대비

  • win rate
  • skill score

  에서 일관된 성능 우위

f) Summary

Chronos-2는

• 세 benchmark 모두에서
• 모든 경쟁 모델을 일관되게 능가

Chronos-Bolt 대비 큰 성능 향상

• (1) Architectural design
• (2) Synthetic multivariate training
• (3) Group attention 기반 ICL

\(\rightarrow\) 이 핵심 요인임을 실증적으로 확인

(2) Improvements with In-context Learning

• Section 5.1
  • full cross learning mode
  • 즉, in-context learning (ICL) 활성화 상태
• Section 5.2:
  • 목적: ICL이 실제로 어디에서, 얼마나 성능 향상을 만드는지
  • univariate inference 대비 효과를 분리해서 분석

Experimental Setup

비교 설정: (1) vs. (2)

• (1) Chronos-2 with ICL
• (2) Chronos-2 univariate inference
  • Batch 내 각 time series를 독립적으로 예측
  • Covariates 존재함에도 불구하고 무시

Subsets of fev-bench

• Univariate subset
  • 32 tasks
  • single target & covariates 없음
• Multivariate subset
  • 26 tasks
  • multiple targets & covariates 없음
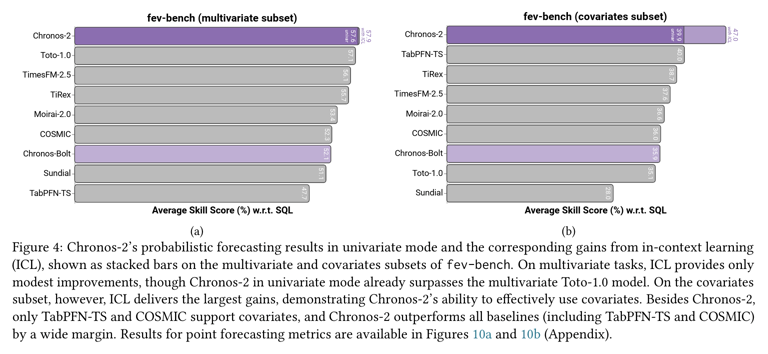
• Covariates subset
  • 42 tasks
  • past-only 또는 known covariates 포함

(3) Ablation Studies