Causal Inference Meets Deep Learning; A Comprehensive Survey - Part 2

Causal Inference Meets Deep Learning: A Comprehensive Survey

4. Standard Paradigms of Causal Intervention

(1) Do-operator

• Represents an “active intervention”
  • \(do(T = t)\) : Sets variable \(T\) to value \(t\)
• Differs from conditioning!!
  • Conditioning = Passively observes \(T = t\) , w/o altering the system
• Why does it differ?
  • \(do(T = t)\) enforces a change \(\rightarrow\) Allowing the study of \(T\)’s causal impact on other variables
• Core tool in causal inference frameworks like SCM

(2) Back-door adjustment

Back-door path

• Path between nodes \(X\) and \(Y\) that begins with an “arrow pointing to \(X\)“
• i.e., \(X \leftarrow Z \rightarrow Y\)

Back-door criterion

• Helps identify valid adjustment sets to estimate causal effects

• If the set of variables \(Z\) satisfies …

  • a) Does not contain descendant nodes of \(X\)
  • b) Blocks every path between \(X\) and \(Y\) that contains a path to \(X\)

  \(\rightarrow\) \(Z\) is said to satisfy the back-door criterion of \((X, Y)\)

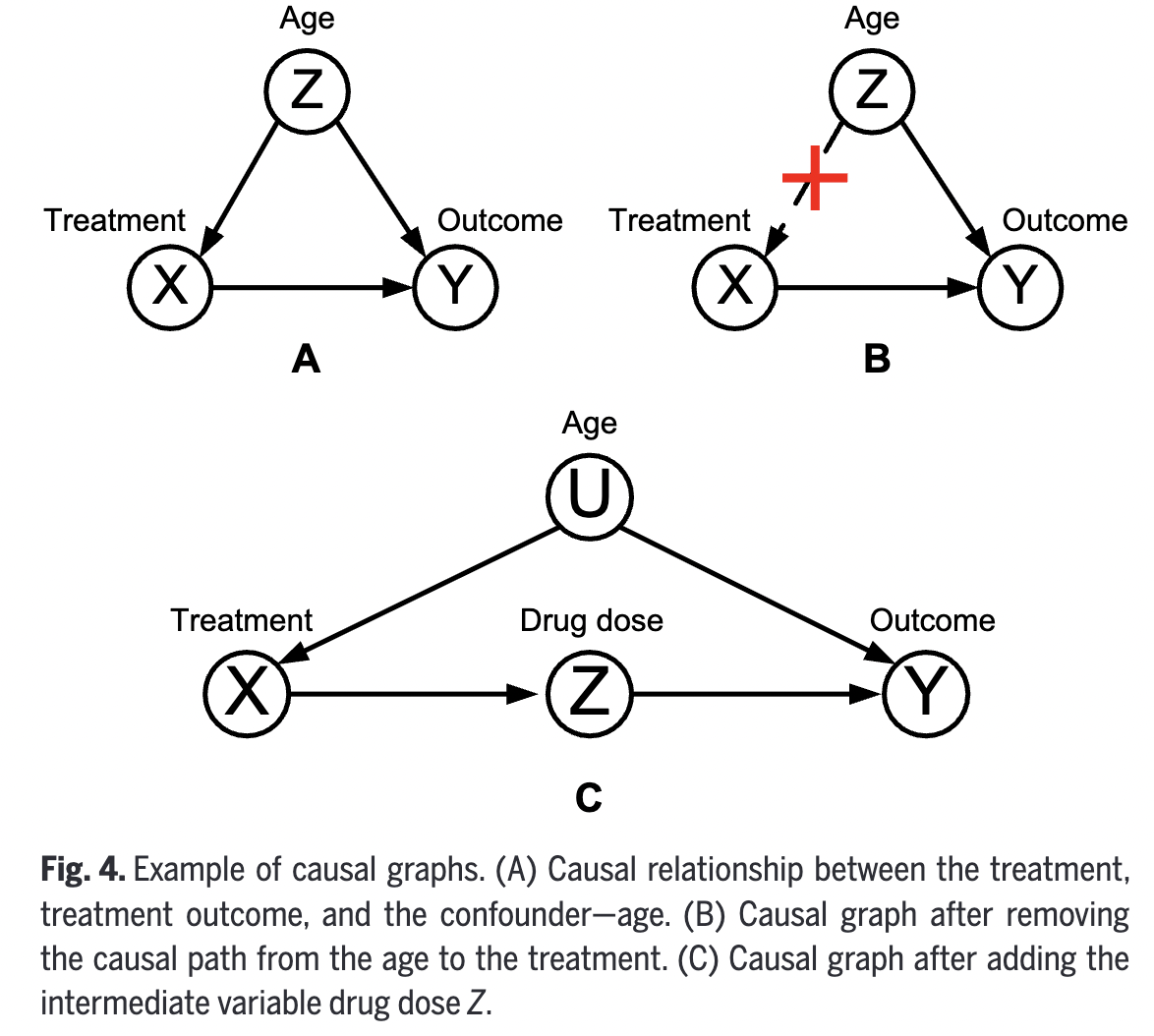
• Example

  • Before) Figure 4(a)
  • Intervention)
    • To investigate the true causal relationship
    • Intervention to eliminate the causal links of confounders to treatment method \(X\)
  • After) Figure 4(b)

Back-door adjustment

• Blocks spurious paths from \(X\) to \(Y\) “by conditioning on \(Z\)“

• Isolates the true causal effect from \(X\) to \(Y\) :)

  ( Prevent distortion from confounders )

Observational vs. Interventional

• Observational conditioning: \(P(Z = z \mid Y = y)\)

• Interventional probability: $$P(Z = z

  do(Y = y))$$

(Note) Do-operator modifies the data distribution by actively setting \(Y = y\)

Four rules for causal inference

Rule 1)

If the variables \(W\) and \(Y\) are unrelated, then:

\(P(Y \mid d o(X), Z, W)=P(Y \mid d o(X), Z)\).

Example) Once we determine the state of the mediator \(Z\) (Smoke) …

\(\rightarrow\) The variable \(W\) (Fire) becomes independent of \(Y\) (Alarm).

Rule 2)

If the variable \(Z\) blocks all back-door paths between \((X, Y)\), then:

\(P(Y \mid d o(X), Z)=P(Y \mid X, Z)\).

Example) If \(Z\) satisfies the back-door criteria from \(X\) to \(Y\),

\(\rightarrow\) Then conditional on \(Z, d o(X)\) is equivalent to \(X\).

Rule 3)

If there is no causal path from \(X\) to \(Y\), then:

\(P(Y \mid d o(X))=P(Y)\).

Example) If there is no causal path from \(X\) to \(Y\),

\(\rightarrow\) Intervening on \(X\) does not impact the probability distribution of \(Y\).

Rule 4)

If there is no confounders between \(X\) and \(Y\), then:

\(P(Y \mid d o(X))=P(Y \mid X)\).

Example) If there are no confounders among the variables

\(\rightarrow\) The intervention does not change the probability distribution

Formula for the corresponding back-door adjustment

\(P(Y=y \mid d o(X=x))=\sum_b P(Y=y \mid X=x, Z=z) P(Z=z)\).

• where \(Z\) meets the back-door criterion of ( \(X, Y\) ).

(3) Front-door adjustment

Front-door path

• Path between node \(X\) and node \(Y\), starting with the arrow pointed from \(X\).
• e.g., \(X \rightarrow Z \rightarrow Y\).

Front-door criterion

Satisfied when the variable set \(Z\) meets the following conditions:

• (a) all paths from \(X\) to \(Y\) are blocked
• (b) there are no back-door paths from \(X\) to \(Z\)
• (c) all back-door paths between \(Z\) and \(Y\) are blocked by \(X\).

Front-door adjustment

• e.g., Add an intermediate variable drug dose \(Z\) between \(X\) and treatment \(Y\).
• Figure 4 (c)
• The causal graph is shown in Fig. 4C. Suppose that data related to age \(U\) are not available, and therefore the true causal effect cannot be obtained by blocking the back-door path \(X \leftarrow U \rightarrow Y\). In such a case, the front-gate adjustment method can be employed.

Formula

\(\begin{aligned} P(Y & =y \mid d o(X=x)) \\ & =\sum_z P(Z=z \mid X=x) \sum_{x^{\prime}} P\left(Y=y \mid X=x^{\prime}, Z=z\right) P\left(X=x^{\prime}\right) \end{aligned}\).

• where \(Z\) satisfies the front-door criterion of \((X, Y)\)

(4) Back-door vs. Front-door

• Back-door adjustment requires identifying “observable confounders” (e.g., \(W\)) btw \(X\) and \(Y\)

• Front-door adjustment uses a “mediating variable” (e.g., \(M\)) when confounders are unobservable

  • “Causal effect” is estimated via \(X → M\) and \(M → Y\) paths

• Real-world data often includes hidden confounders

  \(\rightarrow\) Make front-door methods more practical in some cases

5. Large Model & Causality

LLMs

• Enable natural language-based, data-driven approaches to causal understanding and reasoning

• LLMs’ capabilities in commonsense, counterfactual, and causal reasoning

\(\rightarrow\) Recent advances emphasize LLMs’ potential in causal discovery & causal inference tasks

(1) Recent advancements in large models

Large models: Classified into LLMs, large vision models, and multimodal models

• (1) LLMs (e.g., GPT series, Bard, Pangu)
  • Trained on large corpora for diverse NLP tasks
• (2) Large vision models (e.g., VIT)
  • Used for tasks like object recognition and tracking
• (3) Multimodal models (e.g., MiniGPT-4, PaLM-E, SORA)
  • Integrate vision, text, and speech data

(2) Can large models perform inference

Large models: Trained on large corpora capturing correlations and (possibly) causal patterns

• Remains uncertain whether LLMs can detect causal direction between variables

Traditional causality approaches

• (1) Statistics-based (numerical)
  • Uses causal graphs to infer relationships from data
• (2) Logic-based (rule-driven)
  • Involves rule-based reasoning to identify cause-effect

LLMs allow causal testing through text input/output without structured preprocessing

• However, it’s unclear if LLMs’ answers stem from true reasoning or surface-level patterns

(3) Causality in large models

Hobbhahn et al.

• Tested whether LLMs can detect causal relationships using natural language prompts.

• Results

  • Larger models like GPT-3 performed better, but interference reduced reasoning performance.
  • This shows that data format, not just content, affects causal reasoning in LLMs.

More advanced models (e.g., GPT-3.5 and GPT-4)

• Show improved reasoning abilities

Kıcıman et al.

• Evaluated LLMs on causal benchmarks and memory-based tests.

• Results

  • GPT-4 performed well in counterfactual reasoning,

    but struggled with tasks requiring human context.

  • When commonsense cues were missing, GPT-4 often gave incorrect or overly literal answers.

Zečević et al.

• Argued that LLMs lack true causal inference due to training on text, “not structured data”

• Still, fine-tuned LLMs can answer many causal questions

  (\(\because\) Training data already encodes causal facts)